2021-2022学年人教版初中数学八年级上册13.3.1等腰三角形的性质公开课课件-(共29张PPT)
文档属性
| 名称 | 2021-2022学年人教版初中数学八年级上册13.3.1等腰三角形的性质公开课课件-(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 21:59:00 | ||
图片预览



文档简介
(共29张PPT)
13.3.1 等腰三角形
第一课时 等腰三角形的性质
第十三章
观赏寻找
下载图片
共同特点
观赏寻找
A
B
C
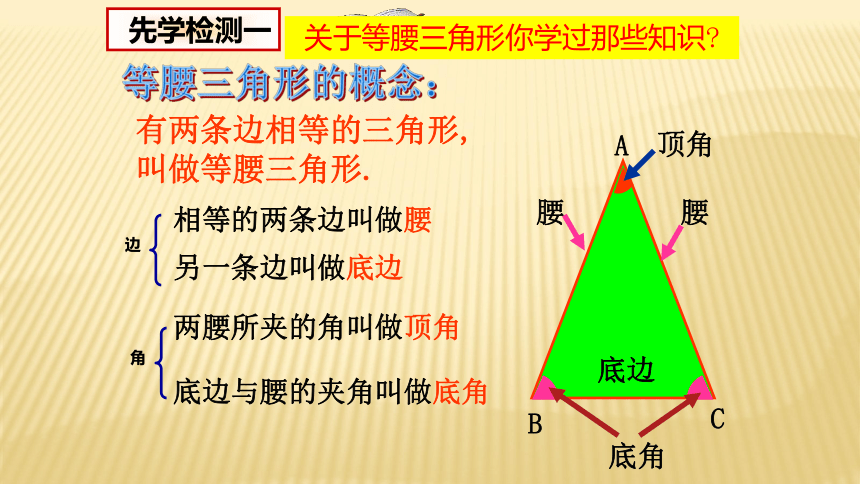
有两条边相等的三角形,
叫做等腰三角形.
等腰三角形的概念:
相等的两条边叫做腰
另一条边叫做底边
底边与腰的夹角叫做底角
两腰所夹的角叫做顶角
腰
腰
底边
顶角
底角
先学检测一
关于等腰三角形你学过那些知识
边
角
A
B
C
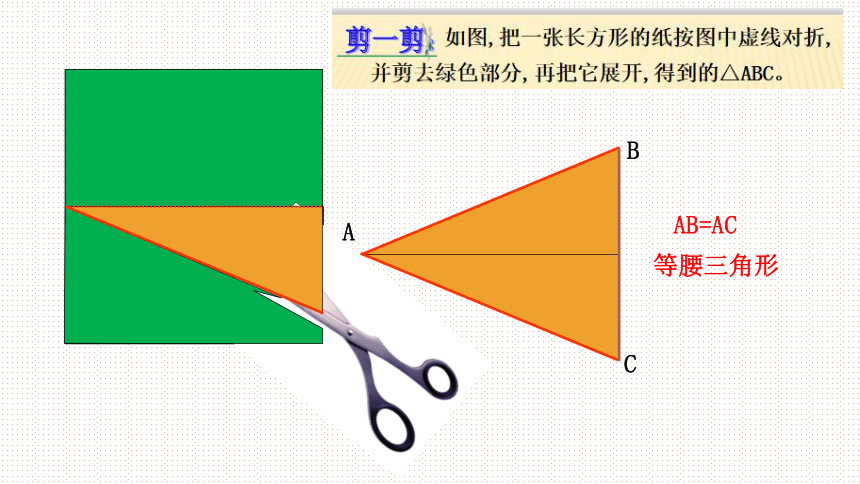
AB=AC
等腰三角形
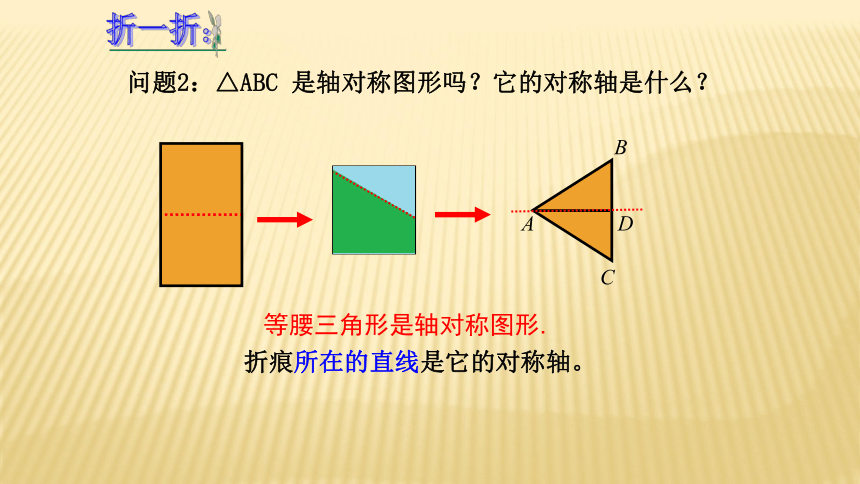
问题2:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折一折:
折痕所在的直线是它的对称轴。
等腰三角形是轴对称图形.
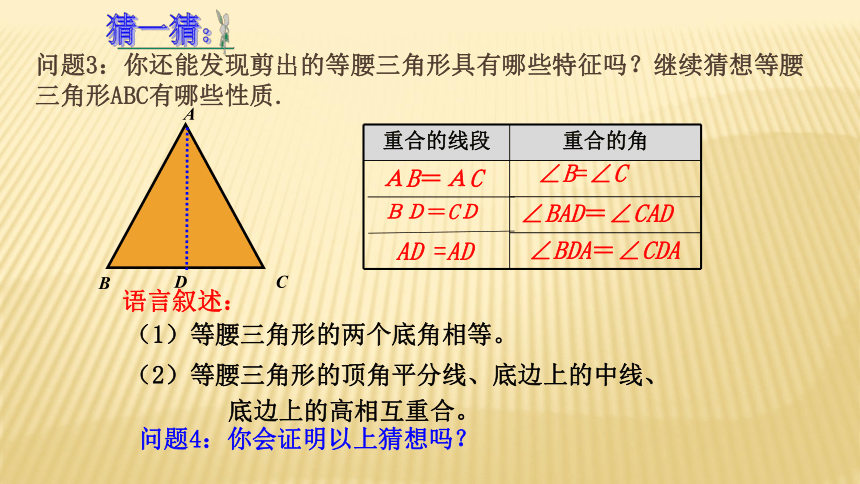
问题3:你还能发现剪出的等腰三角形具有哪些特征吗?继续猜想等腰三角形ABC有哪些性质.
重合的线段 重合的角
∠B=∠C
BD=CD
∠BAD=∠CAD
∠BDA=∠CDA
AB=AC
A
C
D
B
猜一猜:
(2)等腰三角形的顶角平分线、底边上的中线、
底边上的高相互重合。
语言叙述:
问题4:你会证明以上猜想吗?
(1)等腰三角形的两个底角相等。
AD =AD
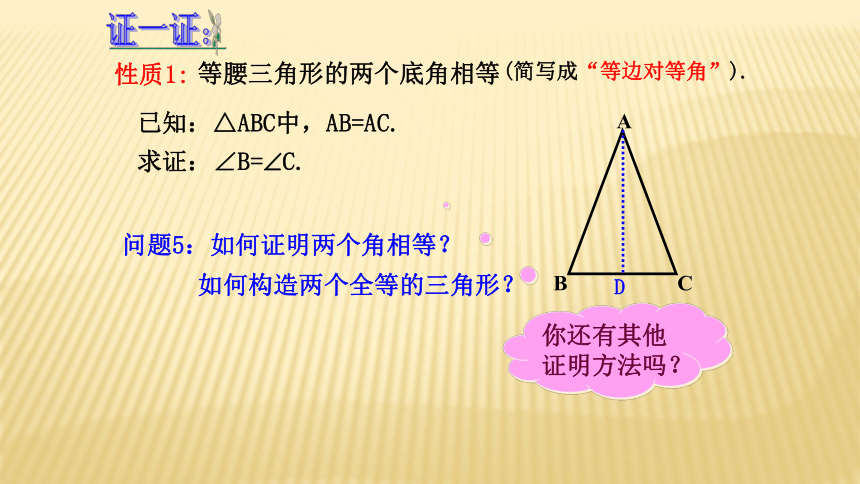
等腰三角形的两个底角相等
已知:△ABC中,AB=AC.
求证:∠B= C.
问题5:如何证明两个角相等?
如何构造两个全等的三角形?
你还有其他证明方法吗?
证一证:
性质1:
(简写成“等边对等角”).
A
B
C
D
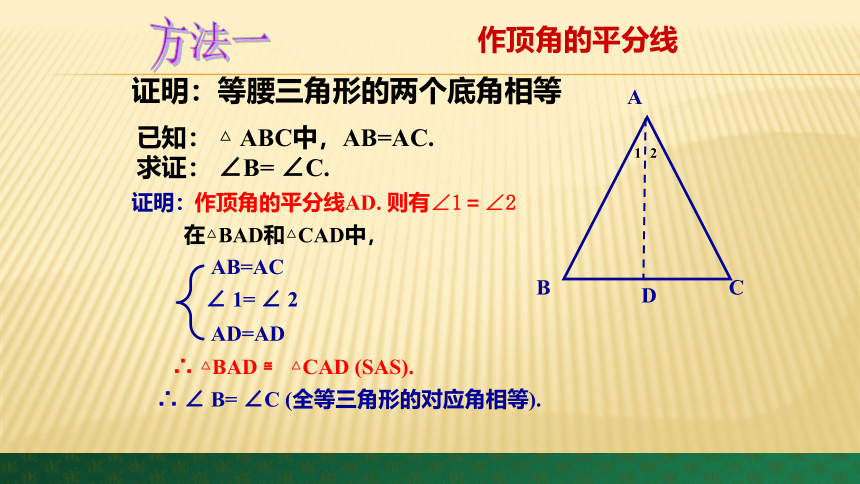
证明:
作顶角的平分线AD. 则有∠1=∠2
AB=AC
∠ 1= ∠ 2
AD=AD
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
1
2
证明:等腰三角形的两个底角相等
作顶角的平分线
D
方法一
在△BAD和△CAD中,
证明:
作底边中线AD, 则BD=CD
AB=AC
BD=CD
AD=AD
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
方法二
在△BAD和△CAD中,
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
证明:
作底边高线AD.
则有∠ADB=∠ADC =90
AB=AC
AD=AD
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
D
证明:等腰三角形的两个底角相等
作底边的高线
在Rt△BAD和△RtCAD中,
方法三
等腰三角形的性质:
等腰三角形的两个底角相等。
性质2
(等边对等角)
A
B
C
D
结论
几何语言:
在△ABC中
∵AB=AC
∴∠B=∠C
D
如图,作底边
的中线AD.
D
如图 作底边
的高AD.
D
如图,作顶角的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见的辅助线
归纳提炼一:
等腰三角形的性质:
性质3
A
B
C
D
结论
等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。
(等腰三角形的“三线合一”)
性质3 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合. (简写成“三线合一” )
(1)∵ AB=AC, AD⊥BC,
∴∠ = ∠ , = .
(2) ∵ AB=AC, BD=CD,
∴ ⊥ ,∠ =∠ .
(3) ∵ AB=AC, ∠1= ∠ 2,
∴ ⊥ , = .
1
2
2
BD
CD
AD
BC
BD
1
BC
AD
CD
几何语言:
A
B
C
D
2
1
知一线得二线
填一填:
∟
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
“三线合一”应该对应等腰三角形的顶角平分线,底边上 的中线和 底边上的高 。
为什么不一样
(1)已知等腰三角形的一个底角是80°,
则其余两角为 .
(2)已知等腰三角形的一个角是80°,
则其余两角为 .
(3)已知等腰三角形的一个角是100°,
则其余两为 .
80° ,20°
80° ,20°
或50°,50°
40° ,40°
对应训练1:
B
C
A
分类讨论
能力提升
1. 在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?
C
B
D
A
1
2
∵ AB=AC ,AD ⊥BC
∴BD=CD
∵BD=2cm
∴CD=2cm BC=4cm
2 4
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
1.图中有哪几个等腰三角形?
A
B
C
D
x
2.有哪些相等的角?
用一用:
方程思想
代数的方法
几何问题
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
∴∠A=36°,∠ABC=∠C=72°.
x
⌒
x
⌒
2x
⌒
⌒
2x
方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
当堂练习
2.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
1.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角
(X)
(X)
(√)
(X)
(√)
3、判断题
4.在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
A
B
C
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
A
B
C
70°或20°
5. 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
图②
图①
证明:(1)如图①,过A作
AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图②
图①
G
等腰三角形
的主要特征
②从角看-------
①从边看-----
③从“三线”看----
④从整体看-------
①分类思想 方程思想
两边相等
两个底角相等
顶角的平分线
底边上的中线
底边上的高相互重合
(三线合一)
轴对称图形
理一理
②等腰三角形常用的辅助线
顶角平分线、底边中线,底边的高
1.知识方面
2.方法方面
完成课时练
布置作业
本节课结束
同学们,再见!
13.3.1 等腰三角形
第一课时 等腰三角形的性质
第十三章
观赏寻找
下载图片
共同特点
观赏寻找
A
B
C
有两条边相等的三角形,
叫做等腰三角形.
等腰三角形的概念:
相等的两条边叫做腰
另一条边叫做底边
底边与腰的夹角叫做底角
两腰所夹的角叫做顶角
腰
腰
底边
顶角
底角
先学检测一
关于等腰三角形你学过那些知识
边
角
A
B
C
AB=AC
等腰三角形
问题2:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折一折:
折痕所在的直线是它的对称轴。
等腰三角形是轴对称图形.
问题3:你还能发现剪出的等腰三角形具有哪些特征吗?继续猜想等腰三角形ABC有哪些性质.
重合的线段 重合的角
∠B=∠C
BD=CD
∠BAD=∠CAD
∠BDA=∠CDA
AB=AC
A
C
D
B
猜一猜:
(2)等腰三角形的顶角平分线、底边上的中线、
底边上的高相互重合。
语言叙述:
问题4:你会证明以上猜想吗?
(1)等腰三角形的两个底角相等。
AD =AD
等腰三角形的两个底角相等
已知:△ABC中,AB=AC.
求证:∠B= C.
问题5:如何证明两个角相等?
如何构造两个全等的三角形?
你还有其他证明方法吗?
证一证:
性质1:
(简写成“等边对等角”).
A
B
C
D
证明:
作顶角的平分线AD. 则有∠1=∠2
AB=AC
∠ 1= ∠ 2
AD=AD
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
1
2
证明:等腰三角形的两个底角相等
作顶角的平分线
D
方法一
在△BAD和△CAD中,
证明:
作底边中线AD, 则BD=CD
AB=AC
BD=CD
AD=AD
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
方法二
在△BAD和△CAD中,
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
证明:
作底边高线AD.
则有∠ADB=∠ADC =90
AB=AC
AD=AD
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
D
证明:等腰三角形的两个底角相等
作底边的高线
在Rt△BAD和△RtCAD中,
方法三
等腰三角形的性质:
等腰三角形的两个底角相等。
性质2
(等边对等角)
A
B
C
D
结论
几何语言:
在△ABC中
∵AB=AC
∴∠B=∠C
D
如图,作底边
的中线AD.
D
如图 作底边
的高AD.
D
如图,作顶角的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见的辅助线
归纳提炼一:
等腰三角形的性质:
性质3
A
B
C
D
结论
等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。
(等腰三角形的“三线合一”)
性质3 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合. (简写成“三线合一” )
(1)∵ AB=AC, AD⊥BC,
∴∠ = ∠ , = .
(2) ∵ AB=AC, BD=CD,
∴ ⊥ ,∠ =∠ .
(3) ∵ AB=AC, ∠1= ∠ 2,
∴ ⊥ , = .
1
2
2
BD
CD
AD
BC
BD
1
BC
AD
CD
几何语言:
A
B
C
D
2
1
知一线得二线
填一填:
∟
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
“三线合一”应该对应等腰三角形的顶角平分线,底边上 的中线和 底边上的高 。
为什么不一样
(1)已知等腰三角形的一个底角是80°,
则其余两角为 .
(2)已知等腰三角形的一个角是80°,
则其余两角为 .
(3)已知等腰三角形的一个角是100°,
则其余两为 .
80° ,20°
80° ,20°
或50°,50°
40° ,40°
对应训练1:
B
C
A
分类讨论
能力提升
1. 在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?
C
B
D
A
1
2
∵ AB=AC ,AD ⊥BC
∴BD=CD
∵BD=2cm
∴CD=2cm BC=4cm
2 4
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
1.图中有哪几个等腰三角形?
A
B
C
D
x
2.有哪些相等的角?
用一用:
方程思想
代数的方法
几何问题
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
∴∠A=36°,∠ABC=∠C=72°.
x
⌒
x
⌒
2x
⌒
⌒
2x
方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
当堂练习
2.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
1.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角
(X)
(X)
(√)
(X)
(√)
3、判断题
4.在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
A
B
C
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
A
B
C
70°或20°
5. 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
图②
图①
证明:(1)如图①,过A作
AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图②
图①
G
等腰三角形
的主要特征
②从角看-------
①从边看-----
③从“三线”看----
④从整体看-------
①分类思想 方程思想
两边相等
两个底角相等
顶角的平分线
底边上的中线
底边上的高相互重合
(三线合一)
轴对称图形
理一理
②等腰三角形常用的辅助线
顶角平分线、底边中线,底边的高
1.知识方面
2.方法方面
完成课时练
布置作业
本节课结束
同学们,再见!
