天津市南开区2021-2022学年高三上学期期末考试数学试题(PDF版含答案)
文档属性
| 名称 | 天津市南开区2021-2022学年高三上学期期末考试数学试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 355.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览


文档简介
天津市南开区 2021 2022学年度第一学期期末 (A) 800 (B) 750 (C) 700 (D) 650
高三数学 2022年 1月 5. 设 log ln 1a = 3 2, b = 2, c = 5 2,则 a, b, c的大小关系为 ( )
试题解答 Mike (A) a < b < c (B) c < a < b (C) b < a < c (D) c < b < a
本试卷分第 I卷(选择题)和第 II卷(非选择题)两部分,共 150分,考试用时 120分钟. 6. 设 P,A,B,C 为球 O表面上的四个点,PA,PB, PC 两两垂直,且 PA = 3, PB = 6,三棱锥 P ABC 的
祝各位考生考试顺利! 体积为 1√8,则球 O的体积为 ( )
第 I卷 23 46 343 √ 243(A) π (B) π (C) 27 6π (D) π
3 6 2
注意事项: ( ) 2π
1. 答第 I卷前,考生务必将自己的姓名、准考号、考试科目涂在答题卡上; 7. 设函数 f(x) = A sin(ωx + φ) A = 0, ω > 0,
π < φ < π 的图象关于直线 x = 对称,它的最小正周期
2 2
为 π,则
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选 ( ) [ ]
3
( )
1 π 2π
(A) f(x)的图象过点 0, ( ) (B) f(x)在 , 上是减函数涂其他答案标号; 2 12 3
5π (π )
3. 本卷共 9小题,每小题 5分,共 45分. (C) f(x)的一个对称中心是 , 0 (D) f(x)的一个对称中心是 , 012 6
参考公式:
x2 y
2 π
8. 已知双曲线 = 1 (a > 0, b > 0),过原点作一条倾斜角 的直线分别交双曲线左、右两支于 P,Q两
球的体积公式 4 3,其中 表示球的半径. a2V = πR R b2 3球 3 点,以线段 PQ为直径的圆过右焦点 F,则双曲线的离心率为 ( )
1 √ √ √ √ 锥体的体积公式 V锥体 = Sh,其中 S 表示锥体的底面积,h表示锥体的高. (A) 3 + 1 (B) 2 + 1 (C) 3 (D) 2
3
一、选择题:{在∣每小题给出的四个}选项中,只有一项是符合题目(要求)的. 9. 函数 f(x) = |2x 3| 8 sinπx (x ∈ R)的所有零点之和为 ( )
1. (A) 10 (B) 11 (C) 12 (D) 13若全集 U = x ∣ 0 < x < 5, x ∈ Z , A = {1, 2}, B = {2, 3},则 UA ∩B = ( )
(A) {2} (B) {3} (C) {4} (D) {2, 3, 4} 第 II卷
2. 设 x ∈ R,则“x2 2x 3”是“2 x 4”的 ( ) 注意事项:
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件 1. 用黑色墨水的钢笔或签字笔答题;
3. 函数 y = 2|x| sin 2x的图象可能是 ( ) 2. 本卷共 11小题,共 105分.
y
y y y 得分 评卷人
二、填空题:本大题共 6个小题,每小题 5分,共 30分.
π O π x π O π x π O π x π O π x 3 + i
10. 设 i为虚数单位,则 = .
( ) 1 + i8
(A) (B) (C) (D) √ 111. 二项式 3 x 的展开式中,常数项是 .
2x
4. 对某种电子元件使用寿命跟踪调查,抽取容量为 1000的样本,其频率分布直方图如图所示.根据此图可知 12. 直线 l : 3x y 6 = 0与圆 x2 + y2 2x 4y = 0相交于 A,B 两点,则 |AB| = .
这批样本中寿命不低于 300 h的电子元件的个数为 ( )
13. 对某实验项目进行测试,测试方法: 共进行 3轮测试; 每轮测试 2次,若至少合格 1次,则本轮通过,
频率 2
组距 否则不通过.已知测试 1次合格的概率为 ,如果各次测试合格与否互不影响,则在一轮测试中,通过的概
1 3
250 率为 ,在 3轮测试中,通过的次数 X 的期望是 .
1 (y + 1)2 (x+ 1)2
400 14. 已知 x > 0, y > 0,则 + 的最小值为 .
3 x y
2000
1 15. # # # # 在四边形 ABCD中,AB = 2DC,AB = 4, BC = AD = 2,则 AC · BD = ;若 E,F 分别是
2000
O 100 200 300 400 500 600 BE AF # # 寿命 (h) 边 BC,AB 上的点,且满足 = = λ,则当 AE ·DF < 0时,λ的取值范围是 .
BC AB
第 1页
三、解答题:本大题共 5小题,共 75分.解答应写出文字说明,证明过程或演算步骤. 得分 评卷人
得分 评卷人
19.(本题满分 15分)
16.(本题满分 14分)
√ 在等比数列 {an}中,a1 = 2,且 a2, a1 + a3, a4依次是等差数列 {bn}的第 2项,第 5项,第 8项.
在△ABC 中,角 A,B,C 所对的边分别为 a, b, c,且 b sinA+ 3a cosB = 0, a = 2c,.
( I ) 求 {an}和 {bn}的通项公式;
( I ) 求角 B;
( II) 设数列 {a2n an}的前 n项和为 Sn.
( II) 求 a, c;
( i) 求 Sn;
(III) 求 cos(2A B)的值. ∑n aibi + 2( ii) 求证: < 6.
i=1 Si
得分 评卷人
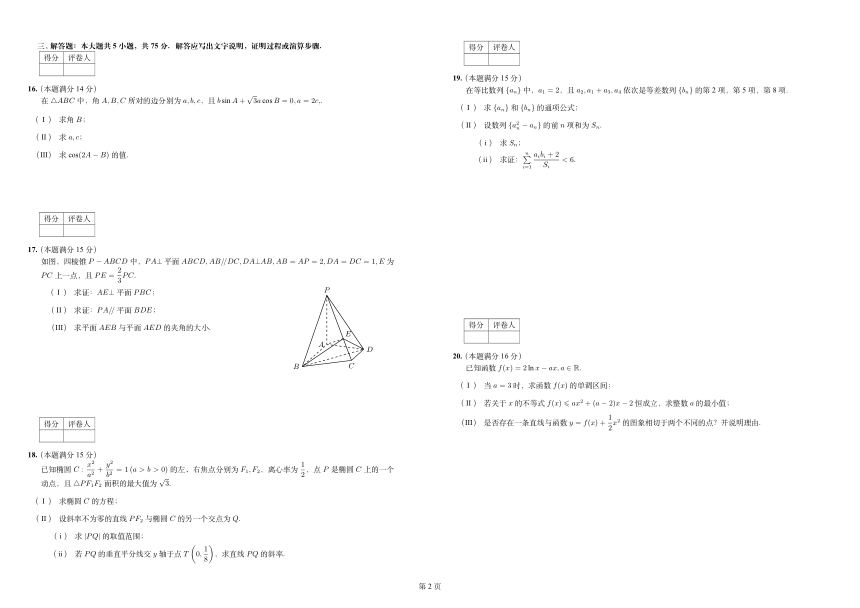
17.(本题满分 15分)
如图,四棱锥 P ABCD中,PA⊥平面 ABCD,AB//DC,DA⊥AB,AB = AP = 2, DA = DC = 1, E 为
2
PC 上一点,且 PE = PC.
3
( I ) 求证:AE⊥平面 PBC; P
( II) 求证:PA//平面 BDE;
(III) 求平面 AEB 与平面 AED的夹角的大小. 得分 评卷人
E
A
D
20.(本题满分 16分)
B C 已知函数 f(x) = 2 lnx ax, a ∈ R.
( I ) 当 a = 3时,求函数 f(x)的单调区间;
( II) 若关于 x的不等式 f(x) ax2 + (a 2)x 2恒成立,求整数 a的最小值;
1
得分 评卷人 (III) 是否存在一条直线与函数 y = f(x) + x2的图象相切于两个不同的点?并说明理由.
2
18.(本题满分 15分)
x2 y2 1
已知椭圆 C : + = 1 (a > b > 0)的左、右焦点分别为 F1, F2,离心率为 ,点 P 是椭圆 C 上的一个
a2 b2 √ 2
动点,且△PF1F2面积的最大值为 3.
( I ) 求椭圆 C 的方程;
( II) 设斜率不为零的直线 PF2与椭圆 C 的另一个交点为 Q.
( i) 求 |PQ|的取值范围; ( )
1
( ii) 若 PQ的垂直平分线交 y轴于点 T 0, ,求直线 PQ的斜率.
8
第 2页
[ ]
天津市南开区 2021 2022学年度第一学期期末 [ π π] π 2π [ π π]所以,当A >[ 0时,]f(x)在 , 上单调递增,在 , 上单调递减.当A < 0时,f(x)在 ,高三数学 参考答案 12 6 6 3 12 6
π 2π
上单调递减,在 (, ) 上单调递增.1. B 6 3 ( )
5π 5π
解:因为 U = {1, 2, 3(, 4}, A) = {1, 2}, C项,因为 f ( ) = A sinπ = 0,所以,( f(x))的一个对称中心是 , 0 .12 12所以, UA = {3, 4}, UA ∩B = {3}. π π π
D项,因为 f = A sin = A,所以 , 0 不是 f(x)的对称中心.
6 2 6
2. D
解:由 x2 2x 3 0得 (x 3)(x+ 1) 0,解得,x 1或 x 3. 8. A
所以,“x2 2x 3”是“2 x 4”的既不充分也不必要条件. 解 1:坐标法设 P (x1, y1),则 Q ( x1, y1).
π √
3. C 因为 直线 PQ过原点,且倾斜角为 ,所以直线 PQ的方程为 y = 3x.解:函数 f(x) = 2|x| sin 2x的定义域为 R. 3√y = 3x,
因为 f( x) = 2| x| sin |x| sin , 由 得 (b2 3a2)x2 = a2( 2x) = 2 2x = f(x) b2.b2x2 a2y2 = a2b2,
所以,f(x)是奇函数,排除 A、B. y
π π 2 a
2b2 (√ )2 2 3a2b2
当 0 < x < 时,sin 2x > 0;当 < x < π时,sin 2x < 0,排除 D,故选 C. 所以,x1 = , y = 3x = .b2 3a2 1 1 b22 2 3a2 Q
( ) 因为以 PQ为直径的圆过点 F,所以,PF⊥FQ.4. A
1 1 3 又因为 F (c, 0),所以,
解:依题意得,不低于 300 h的电子元件个数为 100× + + × 1000 = 800.
400 250 2000 O F x
# · # FP FQ =(x1 c, y1) · ( x1 c, y1)
5. B
=c2 x21 y21
解:因为 P
1 √
2 2 2 2
=c2log log log
a b 3a b
= 3 3 < a = 3 2 < 3 3 = 1, b2 3a2 b2 3a22
√ =0.1
= ln e < ln 2 < ln e = 1.
2 所以,c2 (c2 4a2) = 4a2 (c2 a2) e2 (e2 4) =(4 (e2 )1).√ √ 2 √
1 1 1 因为双曲线的离心率 e > 1,所以 e2 = 4 + 2 3 = 3 + 1 ,解得 e = 3 + 1.
0 < 5 2 = √ < ,
5 2 解 2:坐标法因为以 PQ为直径的圆过点 F,
且 log3 2 < ln 2,所以 c < a < b,选 B. 所以,PF⊥FQ且 |OQ| = |OP | = |OF | = c,O为坐标原点.
π
6. D 因为 ∠QOF = ,3
1 ( )
解: √依题意得, PA · PB · PC = 18.
△ c 3c c
2
3c
2 e2 3e
2
6 所以, OFQ为等边三角形,Q , 代入双曲线方程得 = 1,即 = 1,
因为 PA = 3, PB = 6, 2 2 4a2 4b2 4 4 (e2 1)√ √
PA2 + PB2 + PC2 9 4 4 729 243
所以PC = 6,球O的半径 解得 e = 3 + 1.R = = ,球O的体积V = πR3 = π× = π.
2 2 3 3 8 2 解 3:双曲线定义设双曲线的左焦点为 F1,连结 F1P, F1Q.
7. C 同解 2得△QOF 为等边三角形,所以,∠QOF 1 = 120 . y
2π
解:因为 f(x)的最小正周期为 π,所以, = π.
| | 因为 |OF1| = |OQ| = c,
Q
ω √
因为 ω > 0,所以 ω = 2, f(x) = A sin(2x+ φ). 所以 ∠F1OQ = ∠OQF1 = 30 ,从而有 QF1⊥QF, |QF1| = 3c.
2π
因为 f(x)的图象关于直线 x = 对称, 因为 |Q(F1| |QF | = 2a,3 √ ) c 2 √ F1 O F x
2π π ( 5π) 所以, 3 1 c = 2a,故 e = = √ = 3 + 1.所以,2× + φ = kπ+ , k ∈ Z,解得 φ = kπ , k ∈ Z. a 3 13 2 6
π π π (π因为 < φ < ,所以 φ = , f(x) = A sin 2x+ . P2 2 6 6 )
π A A
A项,因为 f(0) = A sin = ,所以,f(x)过点 0, .
6 2 2 9. C
π π 3π π 2π
B项,由 2kπ+ 2x+ 2kπ+ , k ∈ Z得 kπ+ x kπ+ , k ∈ Z.
2 6 2 6 3 解:由 f(x) = 0得 |2x 3| = 8 sinπx.
第 3页
( )
y 2
设 g(x) = | 32x 3|, h(x) = 8 sinπx,则 g(x)的图象关于 1 8x = 对称. 说明:也可以利用对立事件求 P (A), P (A) = 1 P (A0) = 1 = .2 3 9
π 1 3 8
由 πx = kπ + , k ∈ Z得 x = k + , k ∈ Z,故 x = 是 h(x)的一条
2 2 2
对称轴. 14. 8
5 11
由 g(x) = 8得 |2x 3| = 8,解得 x = 或 x = .
2 2 解:
5 1 7
在同一平面直角坐标系中作出函数 y = g(x)与 y = h(x)的图象,如图 2 2 2 (y + 1)2 (x+ 1)2 y2 + 1 + 2y x2 + 1 + 2x
3O 1 3 5 9 x + = + x y x y
不妨设 8个零点为 xi, i = 1, 2, 3, · · · , 8,且设 x1 < x2 < x3 < · · · < x8. 2 2 2 2 2
2y + 2y 2x+ 2x+
3 x y
由对称性知,x1 + x8 = x2 + x7 = x3 + x6 = x4 + x5 = 2× = 3.
2 4y 4x
= +
所以,x1 + x2 + x3 + · · ·+ x8 = 4× 3 = 12,选 C. x y
4y 4x 8 2 ·x y
10. 2 i =8.
3 + i (3 + i)(1 i) 4 2i
解: = = = 2 i.
1 + i (1 + i)(1 i) 2
当且仅当 x = y = 1时等号成立.
11. 7 ( )8 ( ) ( )k ( )k1 8 k
解:二项式 1x 3 x 1 的通项 T = Ck 1 1 1 8 4kk+1 38 x x 1 = Ck8x 3 3 .2 2 2 [ √ )
7 33
8
由 4k = 0(得 k = 2.3 3 )8 ( )
15. 6, λ ∈ 0,
4
√ 21 1
所以,二项式 3 x 展开式中的常数项是 C2 = 7. 解:(1)依题意可知四边形 ABCD为底角是 60 的等腰梯形.
2x 8 2
√ # # # #
1 # # # # . D CAC = AD +DC = AD + AB,BD = AD AB
12. 10 2
√ # # # # 1
解:圆 x2 + y2 2x 4y = 0的标准方程为 (x √1)
2 + (y 2)2 = 5,其圆心为 (1, 2),半径 r = 5. 因为 AB ·AD = |AB||AD| cos∠BAD = 4× 2× = 4,所以,2 E
|3 2 6| 5 10
圆心 (1, 2)到直线 l的距离 d = √ = . A F B
32√ √ + ( 1)
2 10
所以,|AB| = 2 r2 d2 = 10. ( )
# · # # 1
( )
# · # # AC BD = AD + AB AD AB
8 8 2
13. ,
9 3 # 2 1 # · # 1 # 2(解) ( =AD AD AB AB:记“)一轮测试中,合格 k次”为事件 Ak, k = 0, 1, 2,“一轮测试中,通过为事件”A,则 P (Ak) = 2 2k 2 k
2 1 2 1 1 2
Ck2 .
=2 × 4 × 4
3 3 2 2
= 6.
P (A) =P (A1 ∪A2)
2 # # # # # ( )因为 DF = AF AD = λAB AD,
=P (A1) ∪ P (A2)
=P (A1) + P ((A2)) 2 # # #
2 1 2 AE =AB +BE
=C12 × +3 3 3 # #( =AB + λBC8 )
= . # # # #
( ) 9 =A(B + λ)BA+AD +DC
8 8 8 λ # #
在 3轮测试中,通过的次数 X B 3, ,其期望 E(X) = 3× = . = 1 AB + λAD.
9 9 3 2
第 4页
( )
所以, [( ) ] II # # # ( ) ( ) 证明: PA = (0, 0, 2), BD = ( 2, 1, 0), B E =
4 2 2
, , .
3 3 3
# · # λ # # · # # AE DF = (1 )AB + λAD λ(AB AD ) # 2 #n ·BD = 0, 2x+ y = 0, 2x y = 0,设平面BDE的法向量为 #n = (x, y, z),则 即 即λ λ # · # 4 2 2 # 2 # 2 2 # · # n BE = 0, x+ y + z = 0, 2x+ y + z = 0.=λ 1( A)B λAD +( λ + )1 AB AD 3 3 32 2 令 x = 1,则 #n = (1, 2, 0)为平面 BDE 的一个法向量.
λ λ # =16λ 1 4λ+ 4× λ2 + 1 因为 PA · #n = 0× 1 + 0× 2 0× 2 = 0,所以,PA⊥ #n .
2 2
2 因为 PA 平(面 BD)E,所以,PA//平面 BDE.= 4λ + 14λ 4.
2 2 2
# # (III
# # #
) 解: AE = , , , AB = (2, 0, 0), AD = (0, 1, 0).因为 AE ·DF < 0, √ √ 3 3 3
2 [ 2 7 33 7 + 33
所以, #
2 2 2
4λ + 14λ 4 < 0 4λ 7λ+)2 > 0,解得 λ < 或 λ > . #u ·AE = 0, x+ y + z = 0, x+ y + z = 0,√ 4 4 设平面AEB的法向量为 #u = (x, y, z),则 即 3 3 3 即7 33 #u · # AB = 0, ∈ x = 0, x = 0.因为 0 λ 1,所以,λ 0, .
4 令 y = 1,则 #u = (0, 1, 1)为平面 AEB 的一个法向量.
说明:本题也可用坐标法解. # · # 2 2 2v AE = 0, x+ y + z = 0, x+ y + z = 0,
2π 11 设平面AED的法向量为 # 16.( I ) ;( II)少条件;(III) v = (x, y, z),则B = 即 3 3 3 即# · # 3 14 v AD = 0, y = 0, y = 0.
√ √ #
( I ) 解:因为 b sinA+ 3a cosB = 0,所以,sinB sinA+ 3 sinA cosB = 0. 令 x = 1,则 v = (1, 0, 1)为平面 AED的一个法向量.
√ √ #u · #2π v 1 1 π
因为 sin ,所以 sin # # A > 0 B = 3 cosB tanB = 3, B = . 所以,cos u , v = = √ √ = ,故平面 AEB 与平面 AED夹角的大小为 .# #
3 |u || v | 2 · 2 2 3
( II) ( ) x2 y2 1 3√ 18.( I ) + = 1;( II)( i)(3, 4);( ii)k = 或 k = .1 4 3 2 2
(III) 由余弦定理得 b2 = a2 + c2 2ac cosB,即 b2 = 4c2 + c2 4c2 × ,所以 b = 7c.
2
√ ( I ) 解:设椭圆 C 的焦距为 2c.√ √ √ 3 1 c 1 √ √所以, 7a = 2b,由正弦定理得 7 sinA√= 2 sinB = 3,故 sinA = √ . 因为椭圆 C 的离心率为 ,所以 = , a = 2c, b = a
2 c2 = 3c.
7 2 a 2
2 1 √
因为 B 为钝角,所以 A为锐角,cosA = 1 sin2 A = √ . 当 P 为椭圆 C 的短轴端点时,△PF1F2的面积取得最大值 × 2c× b = bc,所以 bc = 3.
7 2
√ √ x2 y24 3 1
所以,sin 2A = 2 sinA cos(A = ,)cos 2A = 2 cos2 A 1 = . 解得 c = 1, b = 3, a = 2,椭圆 C 的方程为 + = 1.7 7 4 3
2π 2π 2π 11所以,cos cos cos cos sin sin . ( II)( i) 由( I )知,F2(1, 0).设直线 PF2的斜率为 k,则直线 PF2的方程为 y = k(x 1), k = 0.(2A B) = 2A = 2A + 2A =3 3 3 14 y = k(x 1),
π 由 得 (4k2 + 3)x2 8k2x+4k2 12 = 0, = 64k4 4 (4k2 + 3) (4k2 12) =
17.( I )见解答;( II)见解答;(III) . 3x23 + 4y2 = 12,
# # #
以 A为原点,分别以 AB,AD,AP 的方向为 x, y, z轴(建立空间)直角坐标系,如图 144 (k2 + 1).
2 2 2 √ 2 2 2
A(0, 0, 0), B(2,(0, 0), C(1), 1, 0), D(0, 1, 0), P (0, 0, 2), E , , .3 3 3 所以,| |
(1 + k )× 144 (k + 1) 12 (1 + k )
PQ = = .
4k2 + 3 4k2 + 3
3
I #
2 2 2 # # 2
( ) 证明: AE = , , , PB = (2, 0, 2), PC = (1, 1, 2). 令 t = 4k + 3 > 3,则 |PQ| = + 3.
3 3 3 t z 3因为中 t > 3,所以 ∈ (0, 1), |PQ| ∈ (3, 4). m# ·
#
PB = 0, P t
设 平面 PBC 的法向量为 m
# = (x, y, z),则 即 ( ii) 设 P (x1, y1) , Q (x , y# 2 2).#
m · PC = 0, ( )8k2 4k2 3k由( i)(知 x)1 + x2 = ,所以线段 PQ的中点M 的坐标为 , . 2x 2z = 0, 4k2 + 3 4k2 + 3 4k2 + 3E 1 3k 2x+ y 2z = 0. 1 + 2 4k + 24k + 3A 因为 T 0, ,所以线段 PQ中垂线的斜率 k 8 4k +3TM = 4k2 = .2
取 x = 1,则m# = (1, 1, 1)为平面 PBC 的一个法向量. D 8 32k
y 4k
2+3
# 2
因为 AE = m# , C 因为直线 TM 与直线 PQ垂直,
3 B 2
# # ⊥ 4k + 24k + 3所以,AE//m,故 AE 平面 PBC. x 所以, × k =
1 3
1,整理得 4k2 8k + 3 = 0,解得 k = 或 k = .
32k2 2 2
第 5页
( )
n+1
19.( I )a = 2n
4 2 1 1
n , , n ∈ N , bn = 2n, n ∈ N ;( II)( i)S = 2n+1n + ;( ii)见解答 因为 h =(2 ln)2 > 0, h(1) = 1 < 0,3 3 2 2
( I ) 设 { }的 公比为 { }的公差为 . 1an q, bn d 所以 h(x)在 , 1 内有唯一一个零点 x0,且 2 lnx0 = x0. 2 b1 + d = 2q, 当 0 < x < x 时,h(x) > 0,从而有 g′0 (x) > 0, g(x)在 (0, x0)内单调递增.
依题意得 b1 + 4d = 2 + 2q2, 解得 q = 2, b1 = 2, d = 2. 当 x > x0时,h(x) < 0,从而有 g′(x) < 0, g(x)在 (x0,+∞)内单调递减.b1 + 7d = 2q3, 2 lnx所以, 0 + 2x0 + 2 x0 + 2x0 + 2 1g(x)max = g (x0) = = = .
x2 0 + 2x x
2 + 2x x
所以,数列 {an}的通项公式为 a = 2nn , n ∈ N , {bn}的通项公式为
0 0 0
bn = 2n, n ∈ N . 0
1
因为 ∈ (1, 2),所以 a 2,整数 a的最小值为 2.
( II)( i)由( I )知 a2n a 2nn = 2 2n = 4n( 2
n
).所( 以,
x0
) 1 2 1 2 ′ 2
Sn =((4 2) + 42 22 + 4)3 (23 + · · ·+ (4n 2n) ) (III) 解:设 F (x) = f(x) + x = 2 lnx+ x ax, x > 0,则 F (x) = + x a.2 2 x
= 4 + 42 + 43 + · · ·+ 4n 2 + 22 + 23 + · · ·+ 2n 假设存在直线 l与函数 y = F (x)的图象切于两个不同的点 (x1, F (x1)) , (x2, F (x2)) , x1 > 0, x2 > 0且
x = x
4 (1 4n) 2 (1 2n) 1 2.
=
1 4 1 2 因为( 1F ′ (x1) = 2 lnx1 +) x21( ax1,所以,)函数 y = F (x) 的图象(在点 (x1, F ()x1)) 处的切线方程为4n+1 22
= 2n+1 + . 1 2 2 13 3 y 2 lnx 21 + x1 ax1 = (+ x1 a (x) x1),整理得 y = + x1 a x+2 lnx1 x
2
2 x x 2 1
2.
1 1
2 1
aibi 2i× 2i + 2 3 (i · 2i+1 + 2) 3 (i · 2i + 1) 3(i+ 1) 3(i+ 2)( ii)由( i)知 同理可得,切线 l方程也为 y = + x2 a x+ 2 lnx2 x
2
2 2.=
S 4i+1
= = = x 2
2i+1 + 2 4i+1i 3× 2i+1 + 2 (2i+1 1) (2i 1) 2i 1 2i+1 1 23 3 2 2 2 2
所以, + x1 a = + x2 a, + x = + x ,
∑ ∑[ ]
1 2
所以, x1 x2 即 x1 x2
n n 1 1
aibi + 2 3(i+ 1) 3(i+ 2)
2 lnx 2 21 x1 2 = 2 lnx2 x2 2. 12 lnx x21 1 = 2 lnx2 1x22.= 2 2 2 2
S 2i 1 2i+1i 1i=1 i=1 2 2 2 (x x
因为 ,所以, 2 1
)
3× 2 3× 3 3× 3 3× 4 · · · 3(n+ 1) 3(n+ 2)
+ x1 = + x2 = x2 x1.
= + + + x1 x2 x1x2
2 1 22 1 22 1 23 1 2n 1 2n+1 1 因为 x1 = x2,所以,x1x2 = 2.
3(n+ 2)
=6 1 1
2n+1 1 又因为 2 lnx1 x21 = 2 lnx2 x22 2 2
,
<6. 1 2 1 4 1 2
( ) ( ) 所以,2 lnx x
2
1 1 = 2 ln × ,整理得 4 lnx1 x22 x 2 x2 2 1
+ 2 ln 2 = 0.
x21 1 1
2 2 2 2
20.( I )单调递增区间为 0, ,单调递减区间为 ,+∞ ;( II)整数 a的最小值为 2;(III) 1 21 设 u(x) = 4 lnx x2 + 4 4 (x 2)2 ln 2, x > 0,则 u′(x) = x = < 0, u(x)在 (0,+∞)
3 3 2 x2 x x3 x3
内单调递减.
( I ) 解: a = 3时,f(x) = 2 lnx 3x, f(x)的定义域为 (0,+∞). (√ ) √ √
因为 u 2 = 4 ln 2 1 + 1 2 ln 2 = 0,所以,u(x)在 (0,+∞)内有唯一零点 2.
f ′
2
(x) = 2 3x3 = . 1 2
√ √
x x 因此,方程 4 lnx x21 1 + 2 ln 2 = 0有唯一解 x1 = 2,此时有 x2 = 2,这与 x1 = x2矛盾.2 x2
′ 2 2
1
由 f (x) > 0得 0 < x < ;由(f ′(x))< 0得 x > . ( ) 13 3 综上,不存在直线 l与函数 y = f(x) + x2的图象切于不同的两点.2
2 2
所以,f(x)的单调递增区间为 0, ,单调递减区间为 ,+∞ .
3 3
( II) 解:由 f(x) ax2 + (a 2)x 2得 a (x2 + 2x) 2 lnx+ 2x+ 2.
2 lnx+ 2x+ 2
因为 x > 0,所以 a .
x2 + 2x
2 lnx+ 2x+ 2 (2x+ 2) ( x 2 lnx)
设 g(x) = , x > 0,则 g′(x) =
x2 + 2x 2 2
.
(x + 2x)
2
设 h(x) = 2 lnx x, x > 0,则 h′(x) = 1 < 0, h(x)单调递减.
x
第 6页
高三数学 2022年 1月 5. 设 log ln 1a = 3 2, b = 2, c = 5 2,则 a, b, c的大小关系为 ( )
试题解答 Mike (A) a < b < c (B) c < a < b (C) b < a < c (D) c < b < a
本试卷分第 I卷(选择题)和第 II卷(非选择题)两部分,共 150分,考试用时 120分钟. 6. 设 P,A,B,C 为球 O表面上的四个点,PA,PB, PC 两两垂直,且 PA = 3, PB = 6,三棱锥 P ABC 的
祝各位考生考试顺利! 体积为 1√8,则球 O的体积为 ( )
第 I卷 23 46 343 √ 243(A) π (B) π (C) 27 6π (D) π
3 6 2
注意事项: ( ) 2π
1. 答第 I卷前,考生务必将自己的姓名、准考号、考试科目涂在答题卡上; 7. 设函数 f(x) = A sin(ωx + φ) A = 0, ω > 0,
π < φ < π 的图象关于直线 x = 对称,它的最小正周期
2 2
为 π,则
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选 ( ) [ ]
3
( )
1 π 2π
(A) f(x)的图象过点 0, ( ) (B) f(x)在 , 上是减函数涂其他答案标号; 2 12 3
5π (π )
3. 本卷共 9小题,每小题 5分,共 45分. (C) f(x)的一个对称中心是 , 0 (D) f(x)的一个对称中心是 , 012 6
参考公式:
x2 y
2 π
8. 已知双曲线 = 1 (a > 0, b > 0),过原点作一条倾斜角 的直线分别交双曲线左、右两支于 P,Q两
球的体积公式 4 3,其中 表示球的半径. a2V = πR R b2 3球 3 点,以线段 PQ为直径的圆过右焦点 F,则双曲线的离心率为 ( )
1 √ √ √ √ 锥体的体积公式 V锥体 = Sh,其中 S 表示锥体的底面积,h表示锥体的高. (A) 3 + 1 (B) 2 + 1 (C) 3 (D) 2
3
一、选择题:{在∣每小题给出的四个}选项中,只有一项是符合题目(要求)的. 9. 函数 f(x) = |2x 3| 8 sinπx (x ∈ R)的所有零点之和为 ( )
1. (A) 10 (B) 11 (C) 12 (D) 13若全集 U = x ∣ 0 < x < 5, x ∈ Z , A = {1, 2}, B = {2, 3},则 UA ∩B = ( )
(A) {2} (B) {3} (C) {4} (D) {2, 3, 4} 第 II卷
2. 设 x ∈ R,则“x2 2x 3”是“2 x 4”的 ( ) 注意事项:
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件 1. 用黑色墨水的钢笔或签字笔答题;
3. 函数 y = 2|x| sin 2x的图象可能是 ( ) 2. 本卷共 11小题,共 105分.
y
y y y 得分 评卷人
二、填空题:本大题共 6个小题,每小题 5分,共 30分.
π O π x π O π x π O π x π O π x 3 + i
10. 设 i为虚数单位,则 = .
( ) 1 + i8
(A) (B) (C) (D) √ 111. 二项式 3 x 的展开式中,常数项是 .
2x
4. 对某种电子元件使用寿命跟踪调查,抽取容量为 1000的样本,其频率分布直方图如图所示.根据此图可知 12. 直线 l : 3x y 6 = 0与圆 x2 + y2 2x 4y = 0相交于 A,B 两点,则 |AB| = .
这批样本中寿命不低于 300 h的电子元件的个数为 ( )
13. 对某实验项目进行测试,测试方法: 共进行 3轮测试; 每轮测试 2次,若至少合格 1次,则本轮通过,
频率 2
组距 否则不通过.已知测试 1次合格的概率为 ,如果各次测试合格与否互不影响,则在一轮测试中,通过的概
1 3
250 率为 ,在 3轮测试中,通过的次数 X 的期望是 .
1 (y + 1)2 (x+ 1)2
400 14. 已知 x > 0, y > 0,则 + 的最小值为 .
3 x y
2000
1 15. # # # # 在四边形 ABCD中,AB = 2DC,AB = 4, BC = AD = 2,则 AC · BD = ;若 E,F 分别是
2000
O 100 200 300 400 500 600 BE AF # # 寿命 (h) 边 BC,AB 上的点,且满足 = = λ,则当 AE ·DF < 0时,λ的取值范围是 .
BC AB
第 1页
三、解答题:本大题共 5小题,共 75分.解答应写出文字说明,证明过程或演算步骤. 得分 评卷人
得分 评卷人
19.(本题满分 15分)
16.(本题满分 14分)
√ 在等比数列 {an}中,a1 = 2,且 a2, a1 + a3, a4依次是等差数列 {bn}的第 2项,第 5项,第 8项.
在△ABC 中,角 A,B,C 所对的边分别为 a, b, c,且 b sinA+ 3a cosB = 0, a = 2c,.
( I ) 求 {an}和 {bn}的通项公式;
( I ) 求角 B;
( II) 设数列 {a2n an}的前 n项和为 Sn.
( II) 求 a, c;
( i) 求 Sn;
(III) 求 cos(2A B)的值. ∑n aibi + 2( ii) 求证: < 6.
i=1 Si
得分 评卷人
17.(本题满分 15分)
如图,四棱锥 P ABCD中,PA⊥平面 ABCD,AB//DC,DA⊥AB,AB = AP = 2, DA = DC = 1, E 为
2
PC 上一点,且 PE = PC.
3
( I ) 求证:AE⊥平面 PBC; P
( II) 求证:PA//平面 BDE;
(III) 求平面 AEB 与平面 AED的夹角的大小. 得分 评卷人
E
A
D
20.(本题满分 16分)
B C 已知函数 f(x) = 2 lnx ax, a ∈ R.
( I ) 当 a = 3时,求函数 f(x)的单调区间;
( II) 若关于 x的不等式 f(x) ax2 + (a 2)x 2恒成立,求整数 a的最小值;
1
得分 评卷人 (III) 是否存在一条直线与函数 y = f(x) + x2的图象相切于两个不同的点?并说明理由.
2
18.(本题满分 15分)
x2 y2 1
已知椭圆 C : + = 1 (a > b > 0)的左、右焦点分别为 F1, F2,离心率为 ,点 P 是椭圆 C 上的一个
a2 b2 √ 2
动点,且△PF1F2面积的最大值为 3.
( I ) 求椭圆 C 的方程;
( II) 设斜率不为零的直线 PF2与椭圆 C 的另一个交点为 Q.
( i) 求 |PQ|的取值范围; ( )
1
( ii) 若 PQ的垂直平分线交 y轴于点 T 0, ,求直线 PQ的斜率.
8
第 2页
[ ]
天津市南开区 2021 2022学年度第一学期期末 [ π π] π 2π [ π π]所以,当A >[ 0时,]f(x)在 , 上单调递增,在 , 上单调递减.当A < 0时,f(x)在 ,高三数学 参考答案 12 6 6 3 12 6
π 2π
上单调递减,在 (, ) 上单调递增.1. B 6 3 ( )
5π 5π
解:因为 U = {1, 2, 3(, 4}, A) = {1, 2}, C项,因为 f ( ) = A sinπ = 0,所以,( f(x))的一个对称中心是 , 0 .12 12所以, UA = {3, 4}, UA ∩B = {3}. π π π
D项,因为 f = A sin = A,所以 , 0 不是 f(x)的对称中心.
6 2 6
2. D
解:由 x2 2x 3 0得 (x 3)(x+ 1) 0,解得,x 1或 x 3. 8. A
所以,“x2 2x 3”是“2 x 4”的既不充分也不必要条件. 解 1:坐标法设 P (x1, y1),则 Q ( x1, y1).
π √
3. C 因为 直线 PQ过原点,且倾斜角为 ,所以直线 PQ的方程为 y = 3x.解:函数 f(x) = 2|x| sin 2x的定义域为 R. 3√y = 3x,
因为 f( x) = 2| x| sin |x| sin , 由 得 (b2 3a2)x2 = a2( 2x) = 2 2x = f(x) b2.b2x2 a2y2 = a2b2,
所以,f(x)是奇函数,排除 A、B. y
π π 2 a
2b2 (√ )2 2 3a2b2
当 0 < x < 时,sin 2x > 0;当 < x < π时,sin 2x < 0,排除 D,故选 C. 所以,x1 = , y = 3x = .b2 3a2 1 1 b22 2 3a2 Q
( ) 因为以 PQ为直径的圆过点 F,所以,PF⊥FQ.4. A
1 1 3 又因为 F (c, 0),所以,
解:依题意得,不低于 300 h的电子元件个数为 100× + + × 1000 = 800.
400 250 2000 O F x
# · # FP FQ =(x1 c, y1) · ( x1 c, y1)
5. B
=c2 x21 y21
解:因为 P
1 √
2 2 2 2
=c2log log log
a b 3a b
= 3 3 < a = 3 2 < 3 3 = 1, b2 3a2 b2 3a22
√ =0.1
= ln e < ln 2 < ln e = 1.
2 所以,c2 (c2 4a2) = 4a2 (c2 a2) e2 (e2 4) =(4 (e2 )1).√ √ 2 √
1 1 1 因为双曲线的离心率 e > 1,所以 e2 = 4 + 2 3 = 3 + 1 ,解得 e = 3 + 1.
0 < 5 2 = √ < ,
5 2 解 2:坐标法因为以 PQ为直径的圆过点 F,
且 log3 2 < ln 2,所以 c < a < b,选 B. 所以,PF⊥FQ且 |OQ| = |OP | = |OF | = c,O为坐标原点.
π
6. D 因为 ∠QOF = ,3
1 ( )
解: √依题意得, PA · PB · PC = 18.
△ c 3c c
2
3c
2 e2 3e
2
6 所以, OFQ为等边三角形,Q , 代入双曲线方程得 = 1,即 = 1,
因为 PA = 3, PB = 6, 2 2 4a2 4b2 4 4 (e2 1)√ √
PA2 + PB2 + PC2 9 4 4 729 243
所以PC = 6,球O的半径 解得 e = 3 + 1.R = = ,球O的体积V = πR3 = π× = π.
2 2 3 3 8 2 解 3:双曲线定义设双曲线的左焦点为 F1,连结 F1P, F1Q.
7. C 同解 2得△QOF 为等边三角形,所以,∠QOF 1 = 120 . y
2π
解:因为 f(x)的最小正周期为 π,所以, = π.
| | 因为 |OF1| = |OQ| = c,
Q
ω √
因为 ω > 0,所以 ω = 2, f(x) = A sin(2x+ φ). 所以 ∠F1OQ = ∠OQF1 = 30 ,从而有 QF1⊥QF, |QF1| = 3c.
2π
因为 f(x)的图象关于直线 x = 对称, 因为 |Q(F1| |QF | = 2a,3 √ ) c 2 √ F1 O F x
2π π ( 5π) 所以, 3 1 c = 2a,故 e = = √ = 3 + 1.所以,2× + φ = kπ+ , k ∈ Z,解得 φ = kπ , k ∈ Z. a 3 13 2 6
π π π (π因为 < φ < ,所以 φ = , f(x) = A sin 2x+ . P2 2 6 6 )
π A A
A项,因为 f(0) = A sin = ,所以,f(x)过点 0, .
6 2 2 9. C
π π 3π π 2π
B项,由 2kπ+ 2x+ 2kπ+ , k ∈ Z得 kπ+ x kπ+ , k ∈ Z.
2 6 2 6 3 解:由 f(x) = 0得 |2x 3| = 8 sinπx.
第 3页
( )
y 2
设 g(x) = | 32x 3|, h(x) = 8 sinπx,则 g(x)的图象关于 1 8x = 对称. 说明:也可以利用对立事件求 P (A), P (A) = 1 P (A0) = 1 = .2 3 9
π 1 3 8
由 πx = kπ + , k ∈ Z得 x = k + , k ∈ Z,故 x = 是 h(x)的一条
2 2 2
对称轴. 14. 8
5 11
由 g(x) = 8得 |2x 3| = 8,解得 x = 或 x = .
2 2 解:
5 1 7
在同一平面直角坐标系中作出函数 y = g(x)与 y = h(x)的图象,如图 2 2 2 (y + 1)2 (x+ 1)2 y2 + 1 + 2y x2 + 1 + 2x
3O 1 3 5 9 x + = + x y x y
不妨设 8个零点为 xi, i = 1, 2, 3, · · · , 8,且设 x1 < x2 < x3 < · · · < x8. 2 2 2 2 2
2y + 2y 2x+ 2x+
3 x y
由对称性知,x1 + x8 = x2 + x7 = x3 + x6 = x4 + x5 = 2× = 3.
2 4y 4x
= +
所以,x1 + x2 + x3 + · · ·+ x8 = 4× 3 = 12,选 C. x y
4y 4x 8 2 ·x y
10. 2 i =8.
3 + i (3 + i)(1 i) 4 2i
解: = = = 2 i.
1 + i (1 + i)(1 i) 2
当且仅当 x = y = 1时等号成立.
11. 7 ( )8 ( ) ( )k ( )k1 8 k
解:二项式 1x 3 x 1 的通项 T = Ck 1 1 1 8 4kk+1 38 x x 1 = Ck8x 3 3 .2 2 2 [ √ )
7 33
8
由 4k = 0(得 k = 2.3 3 )8 ( )
15. 6, λ ∈ 0,
4
√ 21 1
所以,二项式 3 x 展开式中的常数项是 C2 = 7. 解:(1)依题意可知四边形 ABCD为底角是 60 的等腰梯形.
2x 8 2
√ # # # #
1 # # # # . D CAC = AD +DC = AD + AB,BD = AD AB
12. 10 2
√ # # # # 1
解:圆 x2 + y2 2x 4y = 0的标准方程为 (x √1)
2 + (y 2)2 = 5,其圆心为 (1, 2),半径 r = 5. 因为 AB ·AD = |AB||AD| cos∠BAD = 4× 2× = 4,所以,2 E
|3 2 6| 5 10
圆心 (1, 2)到直线 l的距离 d = √ = . A F B
32√ √ + ( 1)
2 10
所以,|AB| = 2 r2 d2 = 10. ( )
# · # # 1
( )
# · # # AC BD = AD + AB AD AB
8 8 2
13. ,
9 3 # 2 1 # · # 1 # 2(解) ( =AD AD AB AB:记“)一轮测试中,合格 k次”为事件 Ak, k = 0, 1, 2,“一轮测试中,通过为事件”A,则 P (Ak) = 2 2k 2 k
2 1 2 1 1 2
Ck2 .
=2 × 4 × 4
3 3 2 2
= 6.
P (A) =P (A1 ∪A2)
2 # # # # # ( )因为 DF = AF AD = λAB AD,
=P (A1) ∪ P (A2)
=P (A1) + P ((A2)) 2 # # #
2 1 2 AE =AB +BE
=C12 × +3 3 3 # #( =AB + λBC8 )
= . # # # #
( ) 9 =A(B + λ)BA+AD +DC
8 8 8 λ # #
在 3轮测试中,通过的次数 X B 3, ,其期望 E(X) = 3× = . = 1 AB + λAD.
9 9 3 2
第 4页
( )
所以, [( ) ] II # # # ( ) ( ) 证明: PA = (0, 0, 2), BD = ( 2, 1, 0), B E =
4 2 2
, , .
3 3 3
# · # λ # # · # # AE DF = (1 )AB + λAD λ(AB AD ) # 2 #n ·BD = 0, 2x+ y = 0, 2x y = 0,设平面BDE的法向量为 #n = (x, y, z),则 即 即λ λ # · # 4 2 2 # 2 # 2 2 # · # n BE = 0, x+ y + z = 0, 2x+ y + z = 0.=λ 1( A)B λAD +( λ + )1 AB AD 3 3 32 2 令 x = 1,则 #n = (1, 2, 0)为平面 BDE 的一个法向量.
λ λ # =16λ 1 4λ+ 4× λ2 + 1 因为 PA · #n = 0× 1 + 0× 2 0× 2 = 0,所以,PA⊥ #n .
2 2
2 因为 PA 平(面 BD)E,所以,PA//平面 BDE.= 4λ + 14λ 4.
2 2 2
# # (III
# # #
) 解: AE = , , , AB = (2, 0, 0), AD = (0, 1, 0).因为 AE ·DF < 0, √ √ 3 3 3
2 [ 2 7 33 7 + 33
所以, #
2 2 2
4λ + 14λ 4 < 0 4λ 7λ+)2 > 0,解得 λ < 或 λ > . #u ·AE = 0, x+ y + z = 0, x+ y + z = 0,√ 4 4 设平面AEB的法向量为 #u = (x, y, z),则 即 3 3 3 即7 33 #u · # AB = 0, ∈ x = 0, x = 0.因为 0 λ 1,所以,λ 0, .
4 令 y = 1,则 #u = (0, 1, 1)为平面 AEB 的一个法向量.
说明:本题也可用坐标法解. # · # 2 2 2v AE = 0, x+ y + z = 0, x+ y + z = 0,
2π 11 设平面AED的法向量为 # 16.( I ) ;( II)少条件;(III) v = (x, y, z),则B = 即 3 3 3 即# · # 3 14 v AD = 0, y = 0, y = 0.
√ √ #
( I ) 解:因为 b sinA+ 3a cosB = 0,所以,sinB sinA+ 3 sinA cosB = 0. 令 x = 1,则 v = (1, 0, 1)为平面 AED的一个法向量.
√ √ #u · #2π v 1 1 π
因为 sin ,所以 sin # # A > 0 B = 3 cosB tanB = 3, B = . 所以,cos u , v = = √ √ = ,故平面 AEB 与平面 AED夹角的大小为 .# #
3 |u || v | 2 · 2 2 3
( II) ( ) x2 y2 1 3√ 18.( I ) + = 1;( II)( i)(3, 4);( ii)k = 或 k = .1 4 3 2 2
(III) 由余弦定理得 b2 = a2 + c2 2ac cosB,即 b2 = 4c2 + c2 4c2 × ,所以 b = 7c.
2
√ ( I ) 解:设椭圆 C 的焦距为 2c.√ √ √ 3 1 c 1 √ √所以, 7a = 2b,由正弦定理得 7 sinA√= 2 sinB = 3,故 sinA = √ . 因为椭圆 C 的离心率为 ,所以 = , a = 2c, b = a
2 c2 = 3c.
7 2 a 2
2 1 √
因为 B 为钝角,所以 A为锐角,cosA = 1 sin2 A = √ . 当 P 为椭圆 C 的短轴端点时,△PF1F2的面积取得最大值 × 2c× b = bc,所以 bc = 3.
7 2
√ √ x2 y24 3 1
所以,sin 2A = 2 sinA cos(A = ,)cos 2A = 2 cos2 A 1 = . 解得 c = 1, b = 3, a = 2,椭圆 C 的方程为 + = 1.7 7 4 3
2π 2π 2π 11所以,cos cos cos cos sin sin . ( II)( i) 由( I )知,F2(1, 0).设直线 PF2的斜率为 k,则直线 PF2的方程为 y = k(x 1), k = 0.(2A B) = 2A = 2A + 2A =3 3 3 14 y = k(x 1),
π 由 得 (4k2 + 3)x2 8k2x+4k2 12 = 0, = 64k4 4 (4k2 + 3) (4k2 12) =
17.( I )见解答;( II)见解答;(III) . 3x23 + 4y2 = 12,
# # #
以 A为原点,分别以 AB,AD,AP 的方向为 x, y, z轴(建立空间)直角坐标系,如图 144 (k2 + 1).
2 2 2 √ 2 2 2
A(0, 0, 0), B(2,(0, 0), C(1), 1, 0), D(0, 1, 0), P (0, 0, 2), E , , .3 3 3 所以,| |
(1 + k )× 144 (k + 1) 12 (1 + k )
PQ = = .
4k2 + 3 4k2 + 3
3
I #
2 2 2 # # 2
( ) 证明: AE = , , , PB = (2, 0, 2), PC = (1, 1, 2). 令 t = 4k + 3 > 3,则 |PQ| = + 3.
3 3 3 t z 3因为中 t > 3,所以 ∈ (0, 1), |PQ| ∈ (3, 4). m# ·
#
PB = 0, P t
设 平面 PBC 的法向量为 m
# = (x, y, z),则 即 ( ii) 设 P (x1, y1) , Q (x , y# 2 2).#
m · PC = 0, ( )8k2 4k2 3k由( i)(知 x)1 + x2 = ,所以线段 PQ的中点M 的坐标为 , . 2x 2z = 0, 4k2 + 3 4k2 + 3 4k2 + 3E 1 3k 2x+ y 2z = 0. 1 + 2 4k + 24k + 3A 因为 T 0, ,所以线段 PQ中垂线的斜率 k 8 4k +3TM = 4k2 = .2
取 x = 1,则m# = (1, 1, 1)为平面 PBC 的一个法向量. D 8 32k
y 4k
2+3
# 2
因为 AE = m# , C 因为直线 TM 与直线 PQ垂直,
3 B 2
# # ⊥ 4k + 24k + 3所以,AE//m,故 AE 平面 PBC. x 所以, × k =
1 3
1,整理得 4k2 8k + 3 = 0,解得 k = 或 k = .
32k2 2 2
第 5页
( )
n+1
19.( I )a = 2n
4 2 1 1
n , , n ∈ N , bn = 2n, n ∈ N ;( II)( i)S = 2n+1n + ;( ii)见解答 因为 h =(2 ln)2 > 0, h(1) = 1 < 0,3 3 2 2
( I ) 设 { }的 公比为 { }的公差为 . 1an q, bn d 所以 h(x)在 , 1 内有唯一一个零点 x0,且 2 lnx0 = x0. 2 b1 + d = 2q, 当 0 < x < x 时,h(x) > 0,从而有 g′0 (x) > 0, g(x)在 (0, x0)内单调递增.
依题意得 b1 + 4d = 2 + 2q2, 解得 q = 2, b1 = 2, d = 2. 当 x > x0时,h(x) < 0,从而有 g′(x) < 0, g(x)在 (x0,+∞)内单调递减.b1 + 7d = 2q3, 2 lnx所以, 0 + 2x0 + 2 x0 + 2x0 + 2 1g(x)max = g (x0) = = = .
x2 0 + 2x x
2 + 2x x
所以,数列 {an}的通项公式为 a = 2nn , n ∈ N , {bn}的通项公式为
0 0 0
bn = 2n, n ∈ N . 0
1
因为 ∈ (1, 2),所以 a 2,整数 a的最小值为 2.
( II)( i)由( I )知 a2n a 2nn = 2 2n = 4n( 2
n
).所( 以,
x0
) 1 2 1 2 ′ 2
Sn =((4 2) + 42 22 + 4)3 (23 + · · ·+ (4n 2n) ) (III) 解:设 F (x) = f(x) + x = 2 lnx+ x ax, x > 0,则 F (x) = + x a.2 2 x
= 4 + 42 + 43 + · · ·+ 4n 2 + 22 + 23 + · · ·+ 2n 假设存在直线 l与函数 y = F (x)的图象切于两个不同的点 (x1, F (x1)) , (x2, F (x2)) , x1 > 0, x2 > 0且
x = x
4 (1 4n) 2 (1 2n) 1 2.
=
1 4 1 2 因为( 1F ′ (x1) = 2 lnx1 +) x21( ax1,所以,)函数 y = F (x) 的图象(在点 (x1, F ()x1)) 处的切线方程为4n+1 22
= 2n+1 + . 1 2 2 13 3 y 2 lnx 21 + x1 ax1 = (+ x1 a (x) x1),整理得 y = + x1 a x+2 lnx1 x
2
2 x x 2 1
2.
1 1
2 1
aibi 2i× 2i + 2 3 (i · 2i+1 + 2) 3 (i · 2i + 1) 3(i+ 1) 3(i+ 2)( ii)由( i)知 同理可得,切线 l方程也为 y = + x2 a x+ 2 lnx2 x
2
2 2.=
S 4i+1
= = = x 2
2i+1 + 2 4i+1i 3× 2i+1 + 2 (2i+1 1) (2i 1) 2i 1 2i+1 1 23 3 2 2 2 2
所以, + x1 a = + x2 a, + x = + x ,
∑ ∑[ ]
1 2
所以, x1 x2 即 x1 x2
n n 1 1
aibi + 2 3(i+ 1) 3(i+ 2)
2 lnx 2 21 x1 2 = 2 lnx2 x2 2. 12 lnx x21 1 = 2 lnx2 1x22.= 2 2 2 2
S 2i 1 2i+1i 1i=1 i=1 2 2 2 (x x
因为 ,所以, 2 1
)
3× 2 3× 3 3× 3 3× 4 · · · 3(n+ 1) 3(n+ 2)
+ x1 = + x2 = x2 x1.
= + + + x1 x2 x1x2
2 1 22 1 22 1 23 1 2n 1 2n+1 1 因为 x1 = x2,所以,x1x2 = 2.
3(n+ 2)
=6 1 1
2n+1 1 又因为 2 lnx1 x21 = 2 lnx2 x22 2 2
,
<6. 1 2 1 4 1 2
( ) ( ) 所以,2 lnx x
2
1 1 = 2 ln × ,整理得 4 lnx1 x22 x 2 x2 2 1
+ 2 ln 2 = 0.
x21 1 1
2 2 2 2
20.( I )单调递增区间为 0, ,单调递减区间为 ,+∞ ;( II)整数 a的最小值为 2;(III) 1 21 设 u(x) = 4 lnx x2 + 4 4 (x 2)2 ln 2, x > 0,则 u′(x) = x = < 0, u(x)在 (0,+∞)
3 3 2 x2 x x3 x3
内单调递减.
( I ) 解: a = 3时,f(x) = 2 lnx 3x, f(x)的定义域为 (0,+∞). (√ ) √ √
因为 u 2 = 4 ln 2 1 + 1 2 ln 2 = 0,所以,u(x)在 (0,+∞)内有唯一零点 2.
f ′
2
(x) = 2 3x3 = . 1 2
√ √
x x 因此,方程 4 lnx x21 1 + 2 ln 2 = 0有唯一解 x1 = 2,此时有 x2 = 2,这与 x1 = x2矛盾.2 x2
′ 2 2
1
由 f (x) > 0得 0 < x < ;由(f ′(x))< 0得 x > . ( ) 13 3 综上,不存在直线 l与函数 y = f(x) + x2的图象切于不同的两点.2
2 2
所以,f(x)的单调递增区间为 0, ,单调递减区间为 ,+∞ .
3 3
( II) 解:由 f(x) ax2 + (a 2)x 2得 a (x2 + 2x) 2 lnx+ 2x+ 2.
2 lnx+ 2x+ 2
因为 x > 0,所以 a .
x2 + 2x
2 lnx+ 2x+ 2 (2x+ 2) ( x 2 lnx)
设 g(x) = , x > 0,则 g′(x) =
x2 + 2x 2 2
.
(x + 2x)
2
设 h(x) = 2 lnx x, x > 0,则 h′(x) = 1 < 0, h(x)单调递减.
x
第 6页
同课章节目录
