2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系课件(20张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系课件(20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
1.3.1空间直角坐标系
新课程标准解读 核心素养
1.了解空间直角坐标系 1.了解空间直角坐标系的建系方式.(直观想象)
2.掌握空间向量的正交分解及其坐标表示.(直观想象)
3.能在空间直角坐标系中求出点的坐标和已知坐标作出点.(直观想象)
2.会用空间直角坐标系刻画点的位置.
空间向量基本定理
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.
把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
|i|=|j|=|k|=1.且i·j=j·k=i·k=0,这是其他一般基底所没有的.
如果三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),
p=xa+yb+zc.
1.空间直角坐标系 (1)定义
在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz.
x
y
z
O
j
i
k
点O叫做原点,向量 都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面, Oyz平面, Oxz平面。它们把空间分成八个部分
x
y
z
O
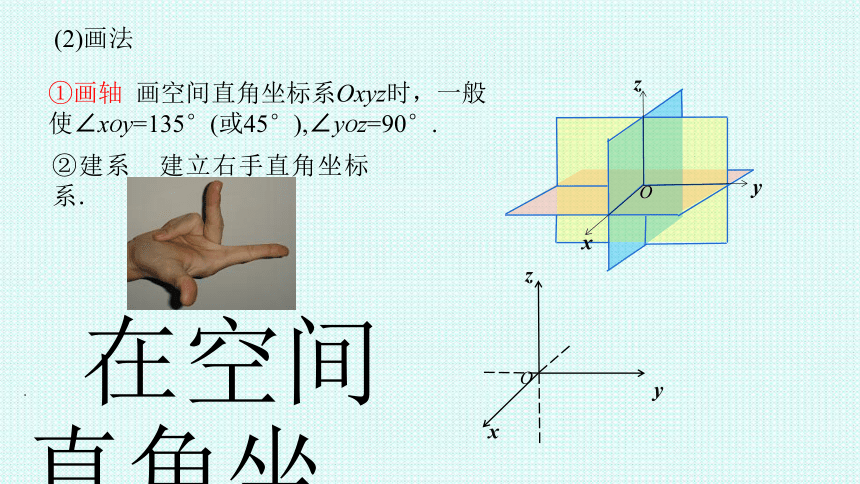
(2)画法
①画轴 画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
②建系 建立右手直角坐标系.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
O
x
y
z
2.点的坐标
在空间直角坐标系Oxyz中,i,j,k为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位置由向量OA唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使OA=xi+yj+zk.
在单位正交基底{i, j, k} 下与向量OA对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中
x叫做点A的横坐标,
y叫做点A的纵坐标,
z叫做点A的竖坐标.
x
y
z
O
A(x,y,z)
i
j
k
3.向量的坐标
在空间直角坐标系Oxyz中,给定向量a,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=xi+yj+zk.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,可简记作a=(x,y,z).
这样在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
x
y
z
O
i
j
k
A(x,y,z)
1、在空间坐标系Oxyz中, ( 分别是与x轴、 y轴、 z轴的正方向相同的单位向量)则AB的坐标为 ,点B的坐标为 。
2、点M(2,-3,-4)在坐标平面xoy、xoz、yoz内的正投影的坐标分别为 ,关于原点的对称点为 ,
关于x轴的对称点为 ,
关于y轴的对称点为 ,
关于z轴的对称点为 ,
(1,-2,-3)
不确定
(2,-3,0)
(2,0,-4)
(0,-3,-4)
(-2, 3,4)
(2, 3, 4)
(-2,-3,4)
(-2,3,-4)
在坐标平面的正投影,缺哪个轴,则该值为0.
关于哪个轴对称,则该值不变,其余互为相反数.
题型一
求空间点的坐标
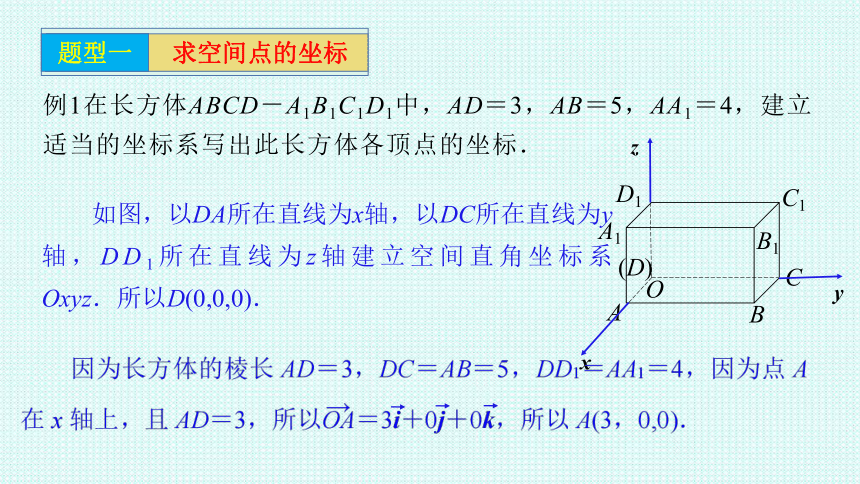
例1在长方体ABCD-A1B1C1D1中,AD=3,AB=5,AA1=4,建立适当的坐标系写出此长方体各顶点的坐标.
C
(D)
A1
B1
C1
D1
A
B
如图,以DA所在直线为x轴,以DC所在直线为y轴,DD1所在直线为z轴建立空间直角坐标系Oxyz.所以D(0,0,0).
O
x
y
z
同理:C(0,5,0),D1(0,0,4).
点B在x轴,y轴,z轴射影分别为A,C,O,它们在坐标轴上的坐标分别为3,5,0,所以点B的坐标为(3,5,0).
同理得A1(3,0,4),C1(0,5,4).
由B1在Oxy平面内的射影为B(3,5,0),
所以B1的横坐标为3,纵坐标为5,
因为B1在z轴上的射影为D1(0,0,4),
所以B1的竖坐标为4,所以点B1的坐标为(3,5,4).
C
(D)
A1
B1
C1
D1
A
B
O
x
y
z
如图所示,四棱锥D OABC中,建立空间直角坐标系Oxyz,若OD=2,OA=4,OC=6,M是BD的中点,求点M的坐标.
A
B
C
O
D
M
z
x
y
法一:点M在x轴,y轴,z轴上的射影分别为M1,M2,M3,它们在坐标轴上的坐标分别为2,3,1,所以点M的坐标是(2,3,1).
如图所示的空间直角坐标系中,四边形ABCD是正方形,AB=2,PA=4,则PD的中点M的坐标为________.
B
A
C
D
P
x
y
z
M
O
点M在x轴、y轴、z轴上的射影分别为M1,O,M2,
题型二
求空间向量的坐标
x
y
z
O
A
B
B1
A1
O1
D
( )
用坐标表示空间向量的步骤
观图形
充分观察图形特征
用运算
建坐标系
根据图形特征建立空间直角坐标系
综合利用向量的加减及数乘运算
将所求的向量用已知的基向量表示出来,确定坐标
定结果
A
B
C
D
M
N
因为PA=AB=AD=1,PA⊥平面ABCD,AB⊥AD,以AD,AB,AP所在直线为坐标轴建立空间直角坐标系如图所示.
x
y
z
题型三
空间向量的坐标应用
角度1 对称问题
在空间直角坐标系中,点P(-2,1,4).
(1)求点P关于x轴的对称点的坐标;
(2)求点P关于Oxy平面的对称点的坐标;
(3)求点P关于点M(2,-1,-4)的对称点的坐标.
(1)由于点P关于x轴对称后,它在x轴的分量不变,在y轴、z轴的分量变为原来的相反数,所以对称点为(-2,-1,-4).
(2)由于点P关于Oxy平面对称后,它在x轴、y轴的分量不变,
在z轴的分量变为原来的相反数,所以对称点为(-2,1,-4).
点M为线段PP1的中点,由中点坐标公式,可得P1(6,-3,-12).
角度2 距离问题
如图所示,在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=2,
点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求线段MN的长度.
C
D
A1
B1
C1
D1
A
B
N
M
如图所示,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴建立空间直角坐标系.
x
y
z
由题意可知C(3,3,0),D(0,3,0),因为|DD1|=|CC1|=|AA1|=2,所以C1(3,3,2),D1(0,3,2),
M是A1C1的三分之一分点且靠近A1点,所以M(1,1,2).
1.3.1空间直角坐标系
新课程标准解读 核心素养
1.了解空间直角坐标系 1.了解空间直角坐标系的建系方式.(直观想象)
2.掌握空间向量的正交分解及其坐标表示.(直观想象)
3.能在空间直角坐标系中求出点的坐标和已知坐标作出点.(直观想象)
2.会用空间直角坐标系刻画点的位置.
空间向量基本定理
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.
把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
|i|=|j|=|k|=1.且i·j=j·k=i·k=0,这是其他一般基底所没有的.
如果三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),
p=xa+yb+zc.
1.空间直角坐标系 (1)定义
在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz.
x
y
z
O
j
i
k
点O叫做原点,向量 都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面, Oyz平面, Oxz平面。它们把空间分成八个部分
x
y
z
O
(2)画法
①画轴 画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
②建系 建立右手直角坐标系.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
O
x
y
z
2.点的坐标
在空间直角坐标系Oxyz中,i,j,k为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位置由向量OA唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使OA=xi+yj+zk.
在单位正交基底{i, j, k} 下与向量OA对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中
x叫做点A的横坐标,
y叫做点A的纵坐标,
z叫做点A的竖坐标.
x
y
z
O
A(x,y,z)
i
j
k
3.向量的坐标
在空间直角坐标系Oxyz中,给定向量a,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=xi+yj+zk.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,可简记作a=(x,y,z).
这样在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.
x
y
z
O
i
j
k
A(x,y,z)
1、在空间坐标系Oxyz中, ( 分别是与x轴、 y轴、 z轴的正方向相同的单位向量)则AB的坐标为 ,点B的坐标为 。
2、点M(2,-3,-4)在坐标平面xoy、xoz、yoz内的正投影的坐标分别为 ,关于原点的对称点为 ,
关于x轴的对称点为 ,
关于y轴的对称点为 ,
关于z轴的对称点为 ,
(1,-2,-3)
不确定
(2,-3,0)
(2,0,-4)
(0,-3,-4)
(-2, 3,4)
(2, 3, 4)
(-2,-3,4)
(-2,3,-4)
在坐标平面的正投影,缺哪个轴,则该值为0.
关于哪个轴对称,则该值不变,其余互为相反数.
题型一
求空间点的坐标
例1在长方体ABCD-A1B1C1D1中,AD=3,AB=5,AA1=4,建立适当的坐标系写出此长方体各顶点的坐标.
C
(D)
A1
B1
C1
D1
A
B
如图,以DA所在直线为x轴,以DC所在直线为y轴,DD1所在直线为z轴建立空间直角坐标系Oxyz.所以D(0,0,0).
O
x
y
z
同理:C(0,5,0),D1(0,0,4).
点B在x轴,y轴,z轴射影分别为A,C,O,它们在坐标轴上的坐标分别为3,5,0,所以点B的坐标为(3,5,0).
同理得A1(3,0,4),C1(0,5,4).
由B1在Oxy平面内的射影为B(3,5,0),
所以B1的横坐标为3,纵坐标为5,
因为B1在z轴上的射影为D1(0,0,4),
所以B1的竖坐标为4,所以点B1的坐标为(3,5,4).
C
(D)
A1
B1
C1
D1
A
B
O
x
y
z
如图所示,四棱锥D OABC中,建立空间直角坐标系Oxyz,若OD=2,OA=4,OC=6,M是BD的中点,求点M的坐标.
A
B
C
O
D
M
z
x
y
法一:点M在x轴,y轴,z轴上的射影分别为M1,M2,M3,它们在坐标轴上的坐标分别为2,3,1,所以点M的坐标是(2,3,1).
如图所示的空间直角坐标系中,四边形ABCD是正方形,AB=2,PA=4,则PD的中点M的坐标为________.
B
A
C
D
P
x
y
z
M
O
点M在x轴、y轴、z轴上的射影分别为M1,O,M2,
题型二
求空间向量的坐标
x
y
z
O
A
B
B1
A1
O1
D
( )
用坐标表示空间向量的步骤
观图形
充分观察图形特征
用运算
建坐标系
根据图形特征建立空间直角坐标系
综合利用向量的加减及数乘运算
将所求的向量用已知的基向量表示出来,确定坐标
定结果
A
B
C
D
M
N
因为PA=AB=AD=1,PA⊥平面ABCD,AB⊥AD,以AD,AB,AP所在直线为坐标轴建立空间直角坐标系如图所示.
x
y
z
题型三
空间向量的坐标应用
角度1 对称问题
在空间直角坐标系中,点P(-2,1,4).
(1)求点P关于x轴的对称点的坐标;
(2)求点P关于Oxy平面的对称点的坐标;
(3)求点P关于点M(2,-1,-4)的对称点的坐标.
(1)由于点P关于x轴对称后,它在x轴的分量不变,在y轴、z轴的分量变为原来的相反数,所以对称点为(-2,-1,-4).
(2)由于点P关于Oxy平面对称后,它在x轴、y轴的分量不变,
在z轴的分量变为原来的相反数,所以对称点为(-2,1,-4).
点M为线段PP1的中点,由中点坐标公式,可得P1(6,-3,-12).
角度2 距离问题
如图所示,在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=2,
点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求线段MN的长度.
C
D
A1
B1
C1
D1
A
B
N
M
如图所示,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴建立空间直角坐标系.
x
y
z
由题意可知C(3,3,0),D(0,3,0),因为|DD1|=|CC1|=|AA1|=2,所以C1(3,3,2),D1(0,3,2),
M是A1C1的三分之一分点且靠近A1点,所以M(1,1,2).
