二次函数学案[1]
图片预览



文档简介
第二章 二次函数
第1节 二次函数所描述的关系
学习目标1.从实际情景中让学生经历探索分析和建立两个变量之间的二次函数关系的过程,进一步体验如何用数学的方法去描述变量之间的数量关系。
2.理解二次函数的概念,掌握二次函数的形式。
3.会建立简单的二次函数的模型,并能根据实际问题确定自变量的取值范围。
学习重点:二次函数的概念和解析式
学习难点:本节“合作学习”涉及的实际问题有的较为复杂,要求学生有较强的概括能力。
学习过程
二次函数的定义
一般地,形如
例如:
在理解二次函数的定义时,应注意以下几点:
(1)任何一个二次函数的关系式都可以化成的形式,因此,把叫做二次函数的一般式,其中分别是二次项、一次项和常数项。
(2)二次函数中,是变量,是常量。自变量x的取值范围是全体实数,b和c可以是任意实数,要特别注意必须是不等于0的实数。因为当=0时,就是,若,则是一次函数;若,则,就是一个常数函数。
(3)二次函数与一元二次方程有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次方程。
■例1下列函数中,y是x的二次函数的是( )
A. B.
C. D.
2、列函数关系式(重点)
函数关系式其实是一个等式,左边字母表示的量随右边的字母变化而变化,所以左边的字母(因为右边的的字母变化它才变化)叫因变量,右边的字母是自己不断的变化,所以叫自变量。
(1)在实际问题中,要表示两个变量间的关系,需找到问题中的等量关系,列出含有这两个变量的二元方程,再按要求化成用含一个变量的式子表示另一个变量的形式。
(2)用尝试求值的方法解决实际问题,可以列出表格,依次对自变量取值,求出它们对应的函数值,然后取得符合题意的值。
■例2正方形的边长为3cm,若它的边长增加xcm,则它的面积就增加ycm。试列出y与x之间的关系式。
典型例题:
题型1根据二次函数的定义确定字母的取值
例1已知是y关于x的二次函数,则m的值是________。
题型2根据变量之间的关系列函数关系式
例2将一根长20cm的铁丝折成一个矩形,设矩形的一边长为xcm,矩形的面积为y cm。
写出y与x之间的关系式,并指出它是一个什么函数?
当边长x=1,2时,矩形的面积分别是多少?
题型3列函数关系式解决实际问题
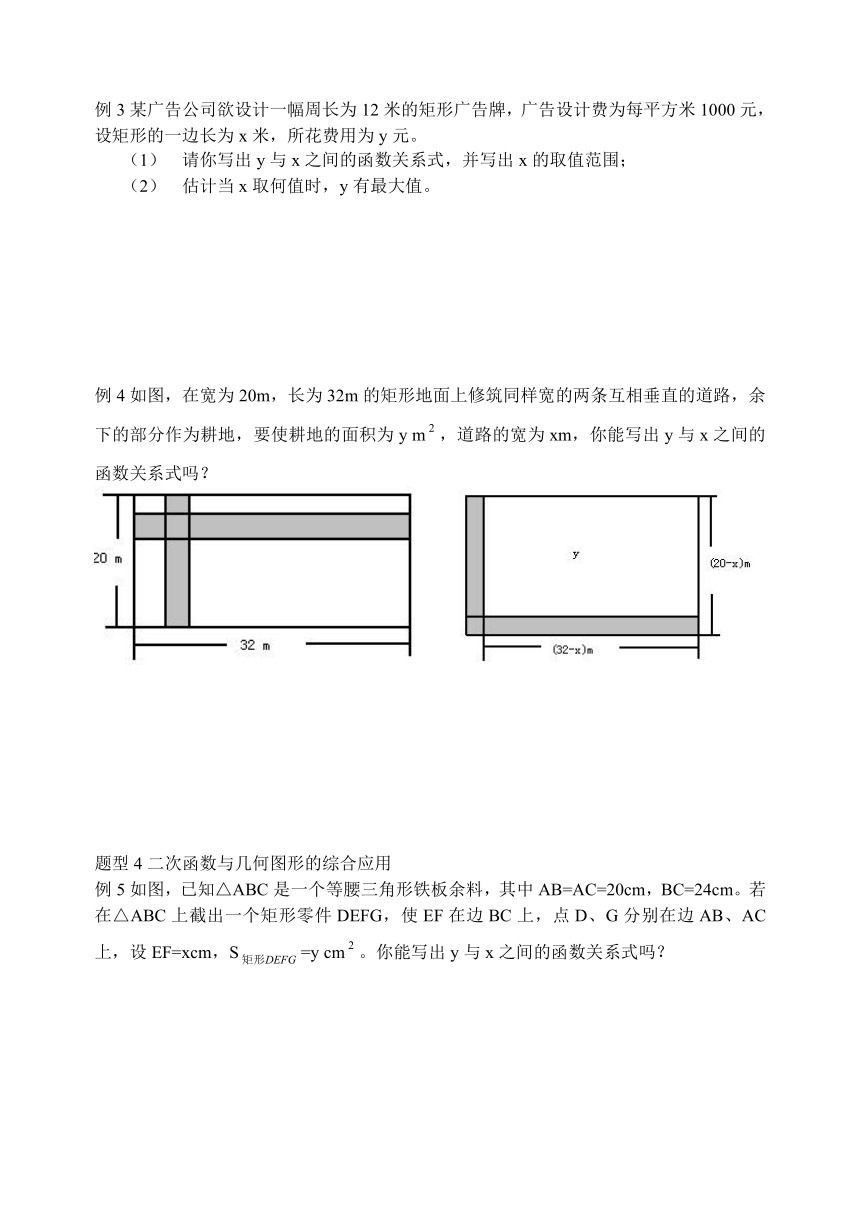
例3某广告公司欲设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形的一边长为x米,所花费用为y元。
请你写出y与x之间的函数关系式,并写出x的取值范围;
估计当x取何值时,y有最大值。
例4如图,在宽为20m,长为32m的矩形地面上修筑同样宽的两条互相垂直的道路,余下的部分作为耕地,要使耕地的面积为y m,道路的宽为xm,你能写出y与x之间的函数关系式吗?
题型4二次函数与几何图形的综合应用
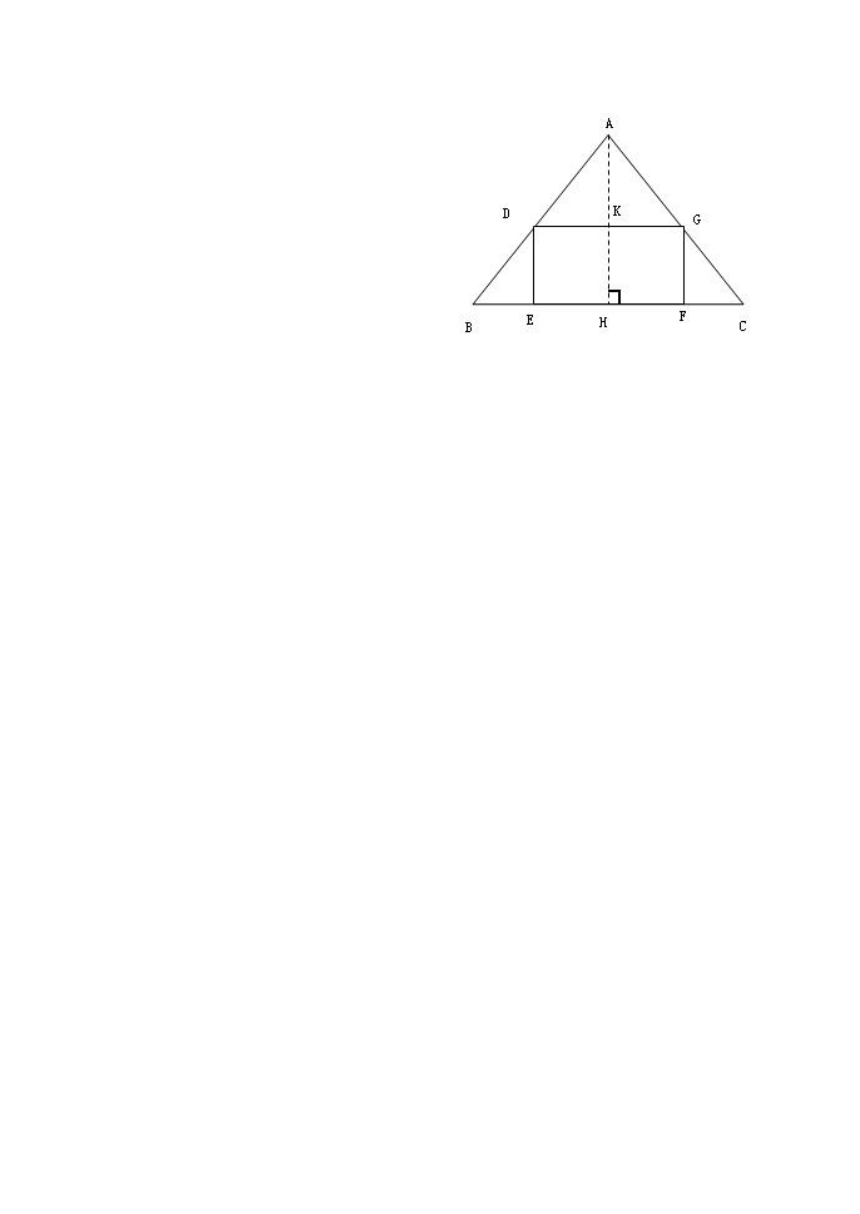
例5如图,已知△ABC是一个等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm。若在△ABC上截出一个矩形零件DEFG,使EF在边BC上,点D、G分别在边AB、AC上,设EF=xcm,S=y cm。你能写出y与x之间的函数关系式吗?
第2节 结识抛物线
学习目标:
1、经历描点法画函数图像的过程;2、学会观察、归纳、概括函数图像的特征;3、
掌握二次函数图像的特征;4、经历从特殊到一般的认识过程,学会合情推理。
学习重点:
型二次函数图像的描绘和图像特征的归纳
学习难点:
选择适当的自变量的值和相应的函数值来画函数图像,该过程较为复杂。
学习过程
二次函数的图象的画法(重点)
描点法:列表——描点——连线
列表——取原点(0,0),然后在原点两侧对称地取4个点
描点——先将y轴右侧的两个点描出来,然后按对称关系找到y轴左侧的两个对应点
连先——按从左到右的顺序将这5个点用平滑的曲线连接起来。注意要“平滑”,且图象不能到“两端”为止,应画成延伸的形状
例1作出二次函数y=的图象。
二次函数的图象的性质(难点)
图象为一条抛物线
轴对称图形,对称轴是y轴,顶点是原点(0,0)——顶点是指对称轴与抛物线的交点。
当>0时,开口向上,在y轴左边,下降趋势;在y轴右边,上升趋势。顶点处取得最小值0。
当<0时,开口向下,在y轴左边,上升趋势;在y轴右边,下降趋势。顶点处取得最大值0。
例2在同一直角坐标系中,画出函数的图象,并根据图象回答下列问题:
说出这两个函数图象的开口方向、对称轴和顶点坐标;
抛物线,当x______时,抛物线上的点都在x轴上方,当x>0时,曲线自左向右逐渐______;它的顶点是图象的最____点;
函数,对于一切x的值,总有函数值y_____0;当x<0时,y随x的增大而____;当x____时,y有最______值,是_______。
典型例题:
例1已知抛物线y=与直线y=3x+m都经过点(2,n)。
求m、n的值。
是否存在另一个交点?若存在,请求出。
例2已知,当m=________时,它的图象是开口向下的抛物线,当x______时,y随x的增大而增大。
例3已知,如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=在第一象限内相交于点P,又知△AOP的面积为4,求的值。
第3节 刹车距离与二次函数
本节内容:
比较的图象的异同(重点)
比较的图象的异同(难点)
1、比较的图象的异同(重点)
二次函数中的的作用:
(1)的符号决定抛物线的开口方向:>0时,开口向上;<0时,开口向下;
(2)的值决定抛物线的形状和开口大小,||相同,抛物线的形状和开口大小相同;||越大,抛物线开口反而越小,图象越靠近y轴。
例1晴天在某段公路上行驶时,速度为v(km/h)的汽车的刹车距离s(m)可由公式确定;雨天行驶时,这一公式为。在同一直角坐标系中作出和的图象。
完成下表:
在图中作出的图象。
解答下列问题:
和的图象有什么相同点与不同点?
如果行车速度是60km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少?你是怎么知道的?
(4)根据上述两点分析,你想对司机师傅说些什么?
2、比较的图象的异同(难点)
二次函数的图象是一条抛物线,它的对称轴是y轴,顶点坐标是(0,c)。对于和的图象,形状相同,只是位置不同。可以看做是把的图象向上(c>0)或向下(c<0)平移|c|个单位长度得到的。
例2在同一直角坐标系中画出函数和的图象,并根据图象回答下列问题。
抛物线经过怎样的平移才能得到抛物线?
函数,当x______时,y随x的增大而减小,当x_____时,函数有最大值,最大值y是______,其图象与y轴的交点坐标是_________,与x轴的交点坐标是________。
(3)试说出抛物线的开口方向,对称轴和顶点坐标。
典型例题:
例1不画图象,说出抛物线和的对称轴、顶点坐标和开口方向。
例2已知函数是关于x的二次函数,求:
满足条件的m值;
m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
m为何值时,函数有最大值,最大值是什么?这时当x为何值时,y随x的增大而减小?
例3心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间满足函数关系:y=-0.1x2+2.6x+43(0≤x≤30),y值越大表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增加?x在什么范围内,学生的接受能力逐步降低?
(2)第10 分钟时,学生的接受能力是多少?几分钟时,学生的接受能力最强?
(3)结合本题针对自己的学习情况有何感受?
第4节 二次函数的图象
本节内容:教学目标:
1、经历二次函数图像平移的过程;理解函数图像平移的意义。
2、了解,,三类二次函数图像之间的关系。
3、会从图像的平移变换的角度认识型二次函数的图像特征。
教学重点:从图像的平移变换的角度认识型二次函数的图像特征。
教学难点:对于平移变换的理解和确定,学生较难理解。
二次函数的图象的平移 配方法及二次函数的图象的基本特征(重点)
二次函数的性质(重点)二次函数的图象特征与的符号之间的关系(难点)
1、二次函数的图象的平移
(1)二次函数的图象可由抛物线向上(或向下)平移而得到。
当k>0时,抛物线向上平移|k|个单位,得的图象;
当k<0时,抛物线向下平移|k|个单位,得的图象。
(2)二次函数的图象可由抛物线向左(或向右)平移而得到。
当h>0时,抛物线向右平移|h|个单位,得到的图象;
当h<0时,抛物线向左平移|h|个单位,得到的图象;
(3)二次函数的图象可由抛物线向左(或向右)平移|h|个单位,再向上(或向下)平移|k|个单位而得到。
注意:
①平移时与上、下、左、右平移的先后许无关。既可先左右后上下,也可先上下后左右;
②抛物线的移动主要看顶点的移动,即在平移时只要抓住顶点的位置变化就可以了;
③抛物线经过反向平移也可得到抛物线的图象。
例1已知是由抛物线向上平移2个单位,再向右平移1个单位得到的抛物线。
求出的值;
在同一直角坐标系中,画出与的图象;
观察的图象,当x______时,y随x的增大而增大,当x______时,函数y有最____值,最_____值是y______;
观察的图象,你能说出对于一切x的值,函数y的取值范围吗?
2、配方法及二次函数的图象的基本特征(重点)
(1)二次函数的一般式与顶点式可互相转化。
①通过去括号,合并同类项可将顶点式化为一般式。
如:
即:可化为
②利用配方法可将一般式转化为顶点式。
如:
因此抛物线的对称轴是直线,顶点坐标是。
(2)二次函数的图象是一条抛物线,它与抛物线的形状相同,只是位置不同,它的对称轴是直线,顶点坐标是。
例2求抛物线的对称轴和顶点坐标。
3、二次函数的性质(重点)
例3画出二次函数的图象,并根据图象说出取何值时,随的增大而增大;取何值时,随的增大而减小?函数y有最大值还是最小值,最值是多少?
4、二次函数的图象特征与的符号之间的关系(难点)
抛物线与其系数、、的符号有着密切的联系。
它们之间的相互制约关系如下表:
例4如图,坐标系中抛物线是函数的图象,则下列式子能成立的是( )
A.
典型例题:
例1指出下列二次函数图象的开口方向、对称轴及顶点坐标。
(1) ; (2) 。
例2如果将抛物线沿直角坐标平面向左平移2个单位长度,再向上平移3个单位长度得到抛物线 。你能确定b、c的值吗?试试看。
例3某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m件与每件的售价x元满足一次函数m=162-3x 。
写出商场卖这种商品每天的销售利润y与每件的售价x之间的函数表达式。
如果商场要想每天获得最大的销售利润,每件商品的售价定为多少合适?最大利润是多少?
例4已知二次函数 ,请你探索一下,当a满足什么条件时,上述函数y的最小值为零。
第5节 用三种方式表示二次函数
本节内容:
二次函数的三种表示方式(重点) 用待定系数法求二次函数的表达式(难点)
1、二次函数的三种表示方式(重点)
二次函数的三种表示方式:
表达式法
表格法
图象法
例1现有铝合金窗框材料8m,准备用它做一个如图长方形窗框(窗框的宽度AB必须小于高度BC)。已知窗台到房屋天花板的距离为2.2m ,设窗框宽AB为x m,窗户的总面积为S(窗框本身及横梁占去的面积忽略不计)。
写出面积S与宽度x的函数关系;
试求出自变量x的取值范围。
2、用待定系数法求二次函数的表达式(难点)
二次函数的表达式有三种形式:
一般式:
已知抛物线上三个点的坐标时。
顶点式:
已知条件与抛物线顶点坐标有关时。
两根式:
已知抛物线与x轴两交点时。
注意:
当抛物线关于y轴对称时,b=0,抛物线为 ;
当抛物线经过原点时 , 抛物线为 ;
当抛物线顶点在原点时 , 抛物线为 。
用待定系数法求函数表达式的一般步骤是:
写出适合的函数表达式;
把已知条件代入函数表达式中,得到关于待定系数的方程或方程组;
解方程(组)求出待定系数的值。即得到函数表达式。
例2已知抛物线的顶点坐标为(-1,-3),与y轴的交点坐标为(0,-5),求抛物线的表达式。
典型例题:
例1已知二次函数过(-1,0),(3,0),(0,),求此抛物线的表达式。
例2已知抛物线的图象如图,该抛物线与x轴交于A、B两点,B点坐标为(,0),则A点坐标为________。
例3二次函数的部分对应值如下表:
二次函数的图象的对称轴为x=______,x=2对应的函数值y=_________。
第6节 何时获得最大利润
本节内容:教学目标:
1、经历数学建模的基本过程。
2、会运用二次函数求实际问题中的最大值或最小值。
3、体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值。
教学重点和难点:
重点:二次函数在最优化问题中的应用。
难点:例1是从现实问题中建立二次函数模型,学生较难理解。
自变量x取全体实数时二次函数的最值 自变量x在一定范围内取值时求二次函数的最值(难点)
二次函数最值的应用问题(重点)
1、自变量x取全体实数时二次函数的最值
求当x取全体实数时y的最值。
有三种方法:
方法1:配方法
当>0,x=时,;
当<0,x=时,。
方法2:公式法 直接利用方法1的结论求最大值与最小值。(即背过方法1)
方法3:判别式法 把y看做已知数,得到。
∵x为全体实数,∴△= → ≥
当>0时,≥,此时y取到最小值为;
当<0时,≤,此时y取到最大值为。
例1求二次函数的最小值。
2、自变量x在一定范围内取值时求二次函数的最值(难点)
分两类情况:
第1类:在范围内时:
(1)若>0,则时,y取到最小值为;
最大值为、中离较远者所对应的y值;
(2)若<0,则时,y取到最大值为;
最小值为、中离较远者所对应的y值;
第2类:不在范围内时:
(1)若>0,< , 则=时,y取到最小值为;
=时,y取到最大值为;
若>0,> , 则=时,y取到最大值为;
=时,y取到最小值为;
(2)若<0,< , 则=时,y取到最大值为;
=时,y取到最小值为;
若<0,> , 则=时,y取到最小值为;
=时,y取到最大值为。
例2分别在写列范围内求函数的最大值或最小值。
(1)0(2)2≤x≤3 。
3、二次函数最值的应用问题(重点)
重点:利用二次函数的最值求实际问题中的最大值或最小值。
一般步骤:
把实际问题转化为二次函数;
利用二次函数的最大值或最小值解决实际问题。
例3某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/kg,下面是他们在活动结束后的对话:
小丽:如果以10元/kg的价格销售,那么每天可售出300kg;
小强:如果以13元/kg的价格销售,那么每天可获取利润750元;
小红:通过调查验证,我发现每天的销售量y(kg)与销售单价x(元)之间存在一次函数关系。
求y(kg)与x(元)(x>0)的函数关系式;
设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?[利润=销售量×(销售单价-进价)]
典型例题:
例1已知二次函数,并且这个函数图象上两点A、B的横坐标分别为=,=4,不求函数值,请比较、的大小。
例2某化工材料经销公司购进一种化工原料7000千克,购进时价格为每千克30元,物价部门规定其销售单价不得高于70元,也不得低于30元,市场调查发现,单价定为70元,日均销售60千克,单价每降低1元,日均多售出2千克。在销售过程中,每天还要支付其他费用500元(天数不足一天时,按整天计算),设销售单价为x元,日均获利为y元。
求y关于x的二次函数表达式,并说明x的取值范围;
将(1)中所求出的二次函数配方写成[或]的形式,写出顶点坐标,并画出图象,由图象指出单价定为多少元时,日均获利最多?最多是多少?
若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种方式,哪种方式获利较多?多多少?
第7节 最大面积是多少
本节内容教学目标:
1、继续经历利用二次函数解决实际最值问题的过程。
2、会综合运用二次函数和其他数学知识解决如有关距离等函数最值问题。
3、发展应用数学解决问题的能力,体会数学与生活的密切联系和数学的应用价值。
教学重点和难点:
重点:利用二次函数的知识对现实问题进行数学地分析,即用数学的方式表示问题以及用数学的方法解决问题。
难点:例3将现实问题数学化,情景比较复杂。
:
长方形的最大面积是多少 卡车过桥问题
1、长方形的最大面积是多少
当题目中要求矩形的最大面积时,通常用含有自变量x的代数式表示矩形的长与宽,根据矩形的面积公式构造关于x的二次函数,再利用二次函数的图象和性质,求出二次函数的最大值,同时要注意自变量的取值范围。
例1如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
求S与x的函数关系式;
如果要围成面积为45平方米的花圃,AB的长是多少米?
能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由。
2、卡车过桥问题
这类问题所给的问题情境常有一个抛物线形桥顶或隧道,已知卡车的高和宽,问卡车是否能完全通过。在问题中,抛物线的函数表达式是首要条件,有时函数表达式已经给出,有时需要先求出来,求出函数表达式后有两种方法可以判断卡车能否从桥下通过:
固定卡车的宽,看桥是否足够高(即相当于告诉x的值,求y的值,然后把限制的高的值与y的值比较大小);
固定卡车的高,看抛物线是否够宽(即相当于告诉y的值,然后再根据函数表达式求x的值,再与限制的宽的值比较大小)。
例2一座拱桥的轮廓是抛物线形,如图1。拱高6m,跨度20m,相邻两支柱间的距离为5m。
将抛物线放在所给的直角坐标系中,如图2。其表达式是的形式,请根据所给数据求出a、c的值;
求支柱MN的长度;
拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排形式宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由。
典型例题:
例1如图,在△ABC中,AF⊥BC,AB=AC=5,BC=6,矩形PQED的边PQ在线段BC上,D、E分别在线段AB、AC上,设BP=x。
求矩形PQED的面积y关于x的函数表达式,并写出自变量x的取值范围;
当x取什么值时,矩形PQED的面积最大?求出这个最大值;
连接PE,当PE∥AB时,矩形PQED的面积是多少?
例2如图,在△ABC中,BC=6,AC=4,∠C=45°,P是BC边上一动点D在AC边上运动,使PD与AB保持平行,设BP=x,△APD的面积为y。求y与x之间的函数关系式,并指出x的取值范围。
第8节 二次函数与一元二次方程
本节内容:
二次函数与一元二次方程的关系(重点)
利用二次函数的图象求一元二次方程的近似根
1、二次函数与一元二次方程的关系(重点)
因为x轴上点的纵坐标都为0,所以求抛物线与x轴交点的坐标,可利用函数表达式来求,只需令y=0,可得一元二次方程。方程的解即为交点的横坐标。
二次函数的图象与x轴的交点有三种情况:
(1)当>0时,方程有两个不相等的实数根、,抛物线与x轴有两个交点(,0)、(,0);
(2)当=0时,方程有两个相等的实数根==,抛物线与x轴有一个交点恰好就是抛物线的顶点(,0);
(3)当<0时,方程没有实数根,抛物线与x轴没有交点。
二次函数与一元二次方程之间的关系如下表:
例1不画图象,判断下列抛物线与x轴交点的个数。
(1) ; (2) ; (3) 。
2、利用二次函数的图象求一元二次方程的近似根
利用二次函数的图象求一元二次方程的近似根的一般步骤:
画出函数的图象;
确定抛物线与x轴交点的个数,看交点在哪两个数之间;
列表,在两个数之间取值估计,并用计算器估算近似根,近似根在对应y值的正负交换的地方,当x由取到时,对应的y值出现>0 ,<0时,则、中必有一个是方程的近似根。再比较||和||,若,则是方程的近似根;若||>||,则是方程的近似根。一般需要我们求近似根的方程,其根往往是无理数,所以列表时不可能取到精确根。
例2已知二次函数的图象如图。则不等式>0的解集是什么?不等式<0的解集是什么?方程=0的解集是什么?
典型例题:
例1若二次函数与x轴有两个交点,求k的取值范围。
例2利用函数的图象,求下列方程的解:
(1) ; (2) 。
例3已知二次函数的部分图象如图。求关于x的一元二次方程的解。
第1节 二次函数所描述的关系
学习目标1.从实际情景中让学生经历探索分析和建立两个变量之间的二次函数关系的过程,进一步体验如何用数学的方法去描述变量之间的数量关系。
2.理解二次函数的概念,掌握二次函数的形式。
3.会建立简单的二次函数的模型,并能根据实际问题确定自变量的取值范围。
学习重点:二次函数的概念和解析式
学习难点:本节“合作学习”涉及的实际问题有的较为复杂,要求学生有较强的概括能力。
学习过程
二次函数的定义
一般地,形如
例如:
在理解二次函数的定义时,应注意以下几点:
(1)任何一个二次函数的关系式都可以化成的形式,因此,把叫做二次函数的一般式,其中分别是二次项、一次项和常数项。
(2)二次函数中,是变量,是常量。自变量x的取值范围是全体实数,b和c可以是任意实数,要特别注意必须是不等于0的实数。因为当=0时,就是,若,则是一次函数;若,则,就是一个常数函数。
(3)二次函数与一元二次方程有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次方程。
■例1下列函数中,y是x的二次函数的是( )
A. B.
C. D.
2、列函数关系式(重点)
函数关系式其实是一个等式,左边字母表示的量随右边的字母变化而变化,所以左边的字母(因为右边的的字母变化它才变化)叫因变量,右边的字母是自己不断的变化,所以叫自变量。
(1)在实际问题中,要表示两个变量间的关系,需找到问题中的等量关系,列出含有这两个变量的二元方程,再按要求化成用含一个变量的式子表示另一个变量的形式。
(2)用尝试求值的方法解决实际问题,可以列出表格,依次对自变量取值,求出它们对应的函数值,然后取得符合题意的值。
■例2正方形的边长为3cm,若它的边长增加xcm,则它的面积就增加ycm。试列出y与x之间的关系式。
典型例题:
题型1根据二次函数的定义确定字母的取值
例1已知是y关于x的二次函数,则m的值是________。
题型2根据变量之间的关系列函数关系式
例2将一根长20cm的铁丝折成一个矩形,设矩形的一边长为xcm,矩形的面积为y cm。
写出y与x之间的关系式,并指出它是一个什么函数?
当边长x=1,2时,矩形的面积分别是多少?
题型3列函数关系式解决实际问题
例3某广告公司欲设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形的一边长为x米,所花费用为y元。
请你写出y与x之间的函数关系式,并写出x的取值范围;
估计当x取何值时,y有最大值。
例4如图,在宽为20m,长为32m的矩形地面上修筑同样宽的两条互相垂直的道路,余下的部分作为耕地,要使耕地的面积为y m,道路的宽为xm,你能写出y与x之间的函数关系式吗?
题型4二次函数与几何图形的综合应用
例5如图,已知△ABC是一个等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm。若在△ABC上截出一个矩形零件DEFG,使EF在边BC上,点D、G分别在边AB、AC上,设EF=xcm,S=y cm。你能写出y与x之间的函数关系式吗?
第2节 结识抛物线
学习目标:
1、经历描点法画函数图像的过程;2、学会观察、归纳、概括函数图像的特征;3、
掌握二次函数图像的特征;4、经历从特殊到一般的认识过程,学会合情推理。
学习重点:
型二次函数图像的描绘和图像特征的归纳
学习难点:
选择适当的自变量的值和相应的函数值来画函数图像,该过程较为复杂。
学习过程
二次函数的图象的画法(重点)
描点法:列表——描点——连线
列表——取原点(0,0),然后在原点两侧对称地取4个点
描点——先将y轴右侧的两个点描出来,然后按对称关系找到y轴左侧的两个对应点
连先——按从左到右的顺序将这5个点用平滑的曲线连接起来。注意要“平滑”,且图象不能到“两端”为止,应画成延伸的形状
例1作出二次函数y=的图象。
二次函数的图象的性质(难点)
图象为一条抛物线
轴对称图形,对称轴是y轴,顶点是原点(0,0)——顶点是指对称轴与抛物线的交点。
当>0时,开口向上,在y轴左边,下降趋势;在y轴右边,上升趋势。顶点处取得最小值0。
当<0时,开口向下,在y轴左边,上升趋势;在y轴右边,下降趋势。顶点处取得最大值0。
例2在同一直角坐标系中,画出函数的图象,并根据图象回答下列问题:
说出这两个函数图象的开口方向、对称轴和顶点坐标;
抛物线,当x______时,抛物线上的点都在x轴上方,当x>0时,曲线自左向右逐渐______;它的顶点是图象的最____点;
函数,对于一切x的值,总有函数值y_____0;当x<0时,y随x的增大而____;当x____时,y有最______值,是_______。
典型例题:
例1已知抛物线y=与直线y=3x+m都经过点(2,n)。
求m、n的值。
是否存在另一个交点?若存在,请求出。
例2已知,当m=________时,它的图象是开口向下的抛物线,当x______时,y随x的增大而增大。
例3已知,如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=在第一象限内相交于点P,又知△AOP的面积为4,求的值。
第3节 刹车距离与二次函数
本节内容:
比较的图象的异同(重点)
比较的图象的异同(难点)
1、比较的图象的异同(重点)
二次函数中的的作用:
(1)的符号决定抛物线的开口方向:>0时,开口向上;<0时,开口向下;
(2)的值决定抛物线的形状和开口大小,||相同,抛物线的形状和开口大小相同;||越大,抛物线开口反而越小,图象越靠近y轴。
例1晴天在某段公路上行驶时,速度为v(km/h)的汽车的刹车距离s(m)可由公式确定;雨天行驶时,这一公式为。在同一直角坐标系中作出和的图象。
完成下表:
在图中作出的图象。
解答下列问题:
和的图象有什么相同点与不同点?
如果行车速度是60km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少?你是怎么知道的?
(4)根据上述两点分析,你想对司机师傅说些什么?
2、比较的图象的异同(难点)
二次函数的图象是一条抛物线,它的对称轴是y轴,顶点坐标是(0,c)。对于和的图象,形状相同,只是位置不同。可以看做是把的图象向上(c>0)或向下(c<0)平移|c|个单位长度得到的。
例2在同一直角坐标系中画出函数和的图象,并根据图象回答下列问题。
抛物线经过怎样的平移才能得到抛物线?
函数,当x______时,y随x的增大而减小,当x_____时,函数有最大值,最大值y是______,其图象与y轴的交点坐标是_________,与x轴的交点坐标是________。
(3)试说出抛物线的开口方向,对称轴和顶点坐标。
典型例题:
例1不画图象,说出抛物线和的对称轴、顶点坐标和开口方向。
例2已知函数是关于x的二次函数,求:
满足条件的m值;
m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
m为何值时,函数有最大值,最大值是什么?这时当x为何值时,y随x的增大而减小?
例3心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间满足函数关系:y=-0.1x2+2.6x+43(0≤x≤30),y值越大表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增加?x在什么范围内,学生的接受能力逐步降低?
(2)第10 分钟时,学生的接受能力是多少?几分钟时,学生的接受能力最强?
(3)结合本题针对自己的学习情况有何感受?
第4节 二次函数的图象
本节内容:教学目标:
1、经历二次函数图像平移的过程;理解函数图像平移的意义。
2、了解,,三类二次函数图像之间的关系。
3、会从图像的平移变换的角度认识型二次函数的图像特征。
教学重点:从图像的平移变换的角度认识型二次函数的图像特征。
教学难点:对于平移变换的理解和确定,学生较难理解。
二次函数的图象的平移 配方法及二次函数的图象的基本特征(重点)
二次函数的性质(重点)二次函数的图象特征与的符号之间的关系(难点)
1、二次函数的图象的平移
(1)二次函数的图象可由抛物线向上(或向下)平移而得到。
当k>0时,抛物线向上平移|k|个单位,得的图象;
当k<0时,抛物线向下平移|k|个单位,得的图象。
(2)二次函数的图象可由抛物线向左(或向右)平移而得到。
当h>0时,抛物线向右平移|h|个单位,得到的图象;
当h<0时,抛物线向左平移|h|个单位,得到的图象;
(3)二次函数的图象可由抛物线向左(或向右)平移|h|个单位,再向上(或向下)平移|k|个单位而得到。
注意:
①平移时与上、下、左、右平移的先后许无关。既可先左右后上下,也可先上下后左右;
②抛物线的移动主要看顶点的移动,即在平移时只要抓住顶点的位置变化就可以了;
③抛物线经过反向平移也可得到抛物线的图象。
例1已知是由抛物线向上平移2个单位,再向右平移1个单位得到的抛物线。
求出的值;
在同一直角坐标系中,画出与的图象;
观察的图象,当x______时,y随x的增大而增大,当x______时,函数y有最____值,最_____值是y______;
观察的图象,你能说出对于一切x的值,函数y的取值范围吗?
2、配方法及二次函数的图象的基本特征(重点)
(1)二次函数的一般式与顶点式可互相转化。
①通过去括号,合并同类项可将顶点式化为一般式。
如:
即:可化为
②利用配方法可将一般式转化为顶点式。
如:
因此抛物线的对称轴是直线,顶点坐标是。
(2)二次函数的图象是一条抛物线,它与抛物线的形状相同,只是位置不同,它的对称轴是直线,顶点坐标是。
例2求抛物线的对称轴和顶点坐标。
3、二次函数的性质(重点)
例3画出二次函数的图象,并根据图象说出取何值时,随的增大而增大;取何值时,随的增大而减小?函数y有最大值还是最小值,最值是多少?
4、二次函数的图象特征与的符号之间的关系(难点)
抛物线与其系数、、的符号有着密切的联系。
它们之间的相互制约关系如下表:
例4如图,坐标系中抛物线是函数的图象,则下列式子能成立的是( )
A.
典型例题:
例1指出下列二次函数图象的开口方向、对称轴及顶点坐标。
(1) ; (2) 。
例2如果将抛物线沿直角坐标平面向左平移2个单位长度,再向上平移3个单位长度得到抛物线 。你能确定b、c的值吗?试试看。
例3某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m件与每件的售价x元满足一次函数m=162-3x 。
写出商场卖这种商品每天的销售利润y与每件的售价x之间的函数表达式。
如果商场要想每天获得最大的销售利润,每件商品的售价定为多少合适?最大利润是多少?
例4已知二次函数 ,请你探索一下,当a满足什么条件时,上述函数y的最小值为零。
第5节 用三种方式表示二次函数
本节内容:
二次函数的三种表示方式(重点) 用待定系数法求二次函数的表达式(难点)
1、二次函数的三种表示方式(重点)
二次函数的三种表示方式:
表达式法
表格法
图象法
例1现有铝合金窗框材料8m,准备用它做一个如图长方形窗框(窗框的宽度AB必须小于高度BC)。已知窗台到房屋天花板的距离为2.2m ,设窗框宽AB为x m,窗户的总面积为S(窗框本身及横梁占去的面积忽略不计)。
写出面积S与宽度x的函数关系;
试求出自变量x的取值范围。
2、用待定系数法求二次函数的表达式(难点)
二次函数的表达式有三种形式:
一般式:
已知抛物线上三个点的坐标时。
顶点式:
已知条件与抛物线顶点坐标有关时。
两根式:
已知抛物线与x轴两交点时。
注意:
当抛物线关于y轴对称时,b=0,抛物线为 ;
当抛物线经过原点时 , 抛物线为 ;
当抛物线顶点在原点时 , 抛物线为 。
用待定系数法求函数表达式的一般步骤是:
写出适合的函数表达式;
把已知条件代入函数表达式中,得到关于待定系数的方程或方程组;
解方程(组)求出待定系数的值。即得到函数表达式。
例2已知抛物线的顶点坐标为(-1,-3),与y轴的交点坐标为(0,-5),求抛物线的表达式。
典型例题:
例1已知二次函数过(-1,0),(3,0),(0,),求此抛物线的表达式。
例2已知抛物线的图象如图,该抛物线与x轴交于A、B两点,B点坐标为(,0),则A点坐标为________。
例3二次函数的部分对应值如下表:
二次函数的图象的对称轴为x=______,x=2对应的函数值y=_________。
第6节 何时获得最大利润
本节内容:教学目标:
1、经历数学建模的基本过程。
2、会运用二次函数求实际问题中的最大值或最小值。
3、体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值。
教学重点和难点:
重点:二次函数在最优化问题中的应用。
难点:例1是从现实问题中建立二次函数模型,学生较难理解。
自变量x取全体实数时二次函数的最值 自变量x在一定范围内取值时求二次函数的最值(难点)
二次函数最值的应用问题(重点)
1、自变量x取全体实数时二次函数的最值
求当x取全体实数时y的最值。
有三种方法:
方法1:配方法
当>0,x=时,;
当<0,x=时,。
方法2:公式法 直接利用方法1的结论求最大值与最小值。(即背过方法1)
方法3:判别式法 把y看做已知数,得到。
∵x为全体实数,∴△= → ≥
当>0时,≥,此时y取到最小值为;
当<0时,≤,此时y取到最大值为。
例1求二次函数的最小值。
2、自变量x在一定范围内取值时求二次函数的最值(难点)
分两类情况:
第1类:在范围内时:
(1)若>0,则时,y取到最小值为;
最大值为、中离较远者所对应的y值;
(2)若<0,则时,y取到最大值为;
最小值为、中离较远者所对应的y值;
第2类:不在范围内时:
(1)若>0,< , 则=时,y取到最小值为;
=时,y取到最大值为;
若>0,> , 则=时,y取到最大值为;
=时,y取到最小值为;
(2)若<0,< , 则=时,y取到最大值为;
=时,y取到最小值为;
若<0,> , 则=时,y取到最小值为;
=时,y取到最大值为。
例2分别在写列范围内求函数的最大值或最小值。
(1)0
3、二次函数最值的应用问题(重点)
重点:利用二次函数的最值求实际问题中的最大值或最小值。
一般步骤:
把实际问题转化为二次函数;
利用二次函数的最大值或最小值解决实际问题。
例3某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/kg,下面是他们在活动结束后的对话:
小丽:如果以10元/kg的价格销售,那么每天可售出300kg;
小强:如果以13元/kg的价格销售,那么每天可获取利润750元;
小红:通过调查验证,我发现每天的销售量y(kg)与销售单价x(元)之间存在一次函数关系。
求y(kg)与x(元)(x>0)的函数关系式;
设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?[利润=销售量×(销售单价-进价)]
典型例题:
例1已知二次函数,并且这个函数图象上两点A、B的横坐标分别为=,=4,不求函数值,请比较、的大小。
例2某化工材料经销公司购进一种化工原料7000千克,购进时价格为每千克30元,物价部门规定其销售单价不得高于70元,也不得低于30元,市场调查发现,单价定为70元,日均销售60千克,单价每降低1元,日均多售出2千克。在销售过程中,每天还要支付其他费用500元(天数不足一天时,按整天计算),设销售单价为x元,日均获利为y元。
求y关于x的二次函数表达式,并说明x的取值范围;
将(1)中所求出的二次函数配方写成[或]的形式,写出顶点坐标,并画出图象,由图象指出单价定为多少元时,日均获利最多?最多是多少?
若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种方式,哪种方式获利较多?多多少?
第7节 最大面积是多少
本节内容教学目标:
1、继续经历利用二次函数解决实际最值问题的过程。
2、会综合运用二次函数和其他数学知识解决如有关距离等函数最值问题。
3、发展应用数学解决问题的能力,体会数学与生活的密切联系和数学的应用价值。
教学重点和难点:
重点:利用二次函数的知识对现实问题进行数学地分析,即用数学的方式表示问题以及用数学的方法解决问题。
难点:例3将现实问题数学化,情景比较复杂。
:
长方形的最大面积是多少 卡车过桥问题
1、长方形的最大面积是多少
当题目中要求矩形的最大面积时,通常用含有自变量x的代数式表示矩形的长与宽,根据矩形的面积公式构造关于x的二次函数,再利用二次函数的图象和性质,求出二次函数的最大值,同时要注意自变量的取值范围。
例1如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
求S与x的函数关系式;
如果要围成面积为45平方米的花圃,AB的长是多少米?
能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由。
2、卡车过桥问题
这类问题所给的问题情境常有一个抛物线形桥顶或隧道,已知卡车的高和宽,问卡车是否能完全通过。在问题中,抛物线的函数表达式是首要条件,有时函数表达式已经给出,有时需要先求出来,求出函数表达式后有两种方法可以判断卡车能否从桥下通过:
固定卡车的宽,看桥是否足够高(即相当于告诉x的值,求y的值,然后把限制的高的值与y的值比较大小);
固定卡车的高,看抛物线是否够宽(即相当于告诉y的值,然后再根据函数表达式求x的值,再与限制的宽的值比较大小)。
例2一座拱桥的轮廓是抛物线形,如图1。拱高6m,跨度20m,相邻两支柱间的距离为5m。
将抛物线放在所给的直角坐标系中,如图2。其表达式是的形式,请根据所给数据求出a、c的值;
求支柱MN的长度;
拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排形式宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由。
典型例题:
例1如图,在△ABC中,AF⊥BC,AB=AC=5,BC=6,矩形PQED的边PQ在线段BC上,D、E分别在线段AB、AC上,设BP=x。
求矩形PQED的面积y关于x的函数表达式,并写出自变量x的取值范围;
当x取什么值时,矩形PQED的面积最大?求出这个最大值;
连接PE,当PE∥AB时,矩形PQED的面积是多少?
例2如图,在△ABC中,BC=6,AC=4,∠C=45°,P是BC边上一动点D在AC边上运动,使PD与AB保持平行,设BP=x,△APD的面积为y。求y与x之间的函数关系式,并指出x的取值范围。
第8节 二次函数与一元二次方程
本节内容:
二次函数与一元二次方程的关系(重点)
利用二次函数的图象求一元二次方程的近似根
1、二次函数与一元二次方程的关系(重点)
因为x轴上点的纵坐标都为0,所以求抛物线与x轴交点的坐标,可利用函数表达式来求,只需令y=0,可得一元二次方程。方程的解即为交点的横坐标。
二次函数的图象与x轴的交点有三种情况:
(1)当>0时,方程有两个不相等的实数根、,抛物线与x轴有两个交点(,0)、(,0);
(2)当=0时,方程有两个相等的实数根==,抛物线与x轴有一个交点恰好就是抛物线的顶点(,0);
(3)当<0时,方程没有实数根,抛物线与x轴没有交点。
二次函数与一元二次方程之间的关系如下表:
例1不画图象,判断下列抛物线与x轴交点的个数。
(1) ; (2) ; (3) 。
2、利用二次函数的图象求一元二次方程的近似根
利用二次函数的图象求一元二次方程的近似根的一般步骤:
画出函数的图象;
确定抛物线与x轴交点的个数,看交点在哪两个数之间;
列表,在两个数之间取值估计,并用计算器估算近似根,近似根在对应y值的正负交换的地方,当x由取到时,对应的y值出现>0 ,<0时,则、中必有一个是方程的近似根。再比较||和||,若,则是方程的近似根;若||>||,则是方程的近似根。一般需要我们求近似根的方程,其根往往是无理数,所以列表时不可能取到精确根。
例2已知二次函数的图象如图。则不等式>0的解集是什么?不等式<0的解集是什么?方程=0的解集是什么?
典型例题:
例1若二次函数与x轴有两个交点,求k的取值范围。
例2利用函数的图象,求下列方程的解:
(1) ; (2) 。
例3已知二次函数的部分图象如图。求关于x的一元二次方程的解。
