2.1向量的加法 课件-2021-2022学年高一下学期数学北师大版(2019)必修第二册(30张ppt)
文档属性
| 名称 | 2.1向量的加法 课件-2021-2022学年高一下学期数学北师大版(2019)必修第二册(30张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
§ 2.1 向量的加法
北师大(2019)必修2
聚焦知识目标
1.掌握向量加法的定义,会用向量加法的三角形法则和向量加法的平行四边形法则作两个向量的和向量.
2.掌握向量加法的交换律和结合律,并会用它们进行向量计算.
聚焦知识目标和数学素养
(1) 掌握向量加法及其几何意义,并会进行向量计算,提升学生的逻辑推理素养;
(2)在向量加法概念形成过程中,理解向量加法概念,培养学生的数学抽象、逻辑推理、数学运算素养;
(3)在概念教学的具体应用中,培养学生的数学建模、直观想象素养。
环节一
情境引入
情境引入
天车是大型生产车间或工地进行起重作业的重要设备.如图,物体在天车的作用下,同时进行竖直方向的宣移和水平方向的位移,
天车
实际位移可以看作竖直方向的位移与水平方向的位移的合成.
位移的合成是以,为邻边的ACBD的对角线,位移的合成遵循平行四边形法则.
环节二
向量加法概念
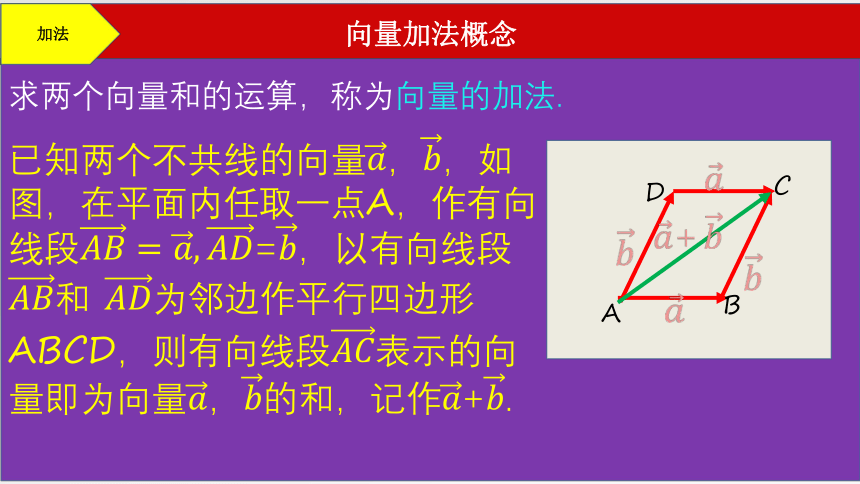
向量加法概念
求两个向量和的运算,称为向量的加法.
已知两个不共线的向量,,如图,在平面内任取一点A,作有向线段=,以有向线段和 为邻边作平行四边形ABCD,则有向线段表示的向量即为向量,的和,记作+.
A
B
D
加法
C
向量加法概念
求两个向量和的运算,称为向量的加法.
已知两个不共线的向量,,如图,在平面内任取一点A,作有向线段=,以有向线段和 为邻边作平行四边形ABCD,则有向线段表示的向量即为向量,的和,记作+.
A
B
D
平行四边形法则
这种求两个向量和的作图方法称为向量加法的平行四边形法则.
C
向量加法概念
显然,如图,作有向线段 以有向线段 ,的终点为起点,作有向线段连接A,C得到有向线段,也可以表示向量与的和
A
B
D
三角形法则
这种求两个向量和的作图方法称为向量加法的三角形法则.
C
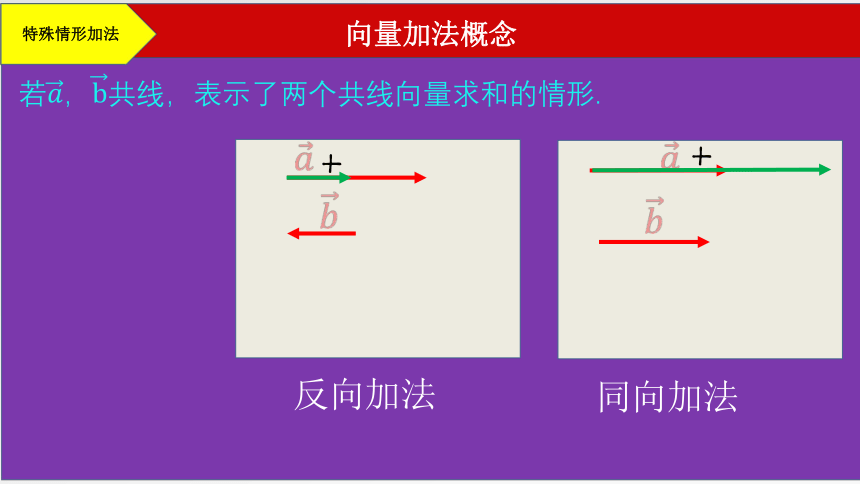
向量加法概念
若,共线,表示了两个共线向量求和的情形.
特殊情形加法
同向加法
+
+
反向加法
向量加法概念
若,共线,表示了两个共线向量求和的情形.
特殊情形加法
也就是说,若两个共线向量方向相同,则它们的和向量方向与原方向一致,大小为两个向量大小之和;若两个共线向量方向相反且大小不相等,则它们的和向量方向向与较大向量的方向一致,大小是两个向量大小差的绝对值
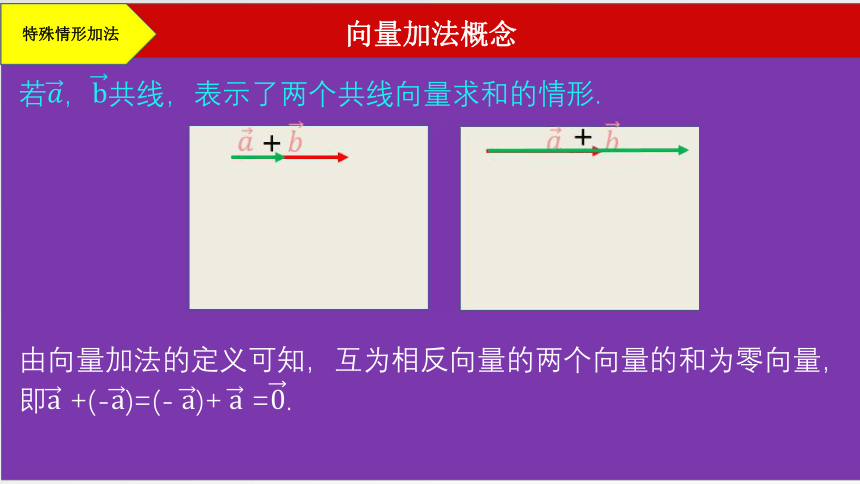
向量加法概念
若,共线,表示了两个共线向量求和的情形.
特殊情形加法
由向量加法的定义可知,互为相反向量的两个向量的和为零向量,即 +(-)=(- )+ =.
环节三
向量加法法则应用
向量的加法法则应用
【例1】 (1)如图①,用向量加法的三角形法则作出a+b;
(2)如图②,用向量加法的平行四边形法则作出a+b.
作图题
向量的加法法则应用
作图题
解后心得
用三角形法则求和向量,关键是抓住“首尾相连”,和向量是第一个向量的起点指向第二个向量的终点,平行四边形法则注意“共起点”.且两种方法中,第一个向量的起点可任意选取,可在某一个向量上,也可在其它位置.两向量共线时,三角形法则仍适用,平行四边形法则不适用.
向量的加法法则应用
练习
向量的加法法则应用
应用题
例2.轮船从A港沿北偏东60°方向行驶了40n mile到达B处,再由B处沿正北方向行驶40n mile到达C处.求此时轮船与A港的相对位置.
解如图,、分别表示轮船的两次位移,则表示轮船的合位移
设正东方向所在直线为AE,过点B作AE的垂线,垂足为点D.
Rt△ADB中,△ADB=90°,△DAB=30° 0nmile.所以 ·sin∠DAB=40·sin30°=20(n mile),
向量的加法法则应用
应用题
例2.轮船从A港沿北偏东60°方向行驶了40n mile到达B处,再由B处沿正北方向行驶40n mile到达C处.求此时轮船与A港的相对位置.
解如图,、分别表示轮船的两次位移,则表示轮船的合位移
设正东方向所在直线为AE,过点B作AE的垂线,垂足为点D.
cos∠DAB=40·cos30°
在Rt△ADC中,△ADC=90°. (n mile),由勾股定理得
环节四
向量加法的运算律
向量加法的运算律
我们熟知,数的加法满足结合律和交换律,即对任意α,β,γ∈R,(a+β)+γ=a+(β+γ),
α+β=β+α.
那么向量的加法运算满足哪些运算律呢?
向量的加法也满足结合律和交换律,即
( +)+ = +( +),+ =+.
向量加法的运算律
先证明向量,. 的加法满足结合律.
证明结合律
向量加法的运算律
再证明向量,的加法满足交换律
证明交换律
向量加法的运算律
例3.已知向量,,如图,求作++.
应用运算律
在平面内任取一点O,作 =, =, =,如图,则由向量加法的三角形法则,得
解后心得
应用运算律
用三角形法则作两向量的和时,要注意两向量“首尾相接”;用平行四边形法则作两向量的和时,要注意保证两向量有公共起点.
2.求作共线向量或多个向量的和向量时,应首选三角形法则,注意和向量的方向是从起始向量的起点指向末尾向量的终点.
向量加法的运算律
怎样求作多个向量的和
思考
(1)由于向量的加法既满足交换律,又满足结合律,因此多个向量的加法运算即可按任意的次序与组合来求作.
(2)向量的多边形法则:
①在平面内任取一点,以此点为起点作第一个向量;
②以第一个向量的终点为起点作第二个向量;
③依次类推,最后以第n-1个向量的终点为起点作第n个向量;
④则以第一个向量的起点为起点,以第n个向量的终点为终点的向量,就是这n个向量的和.
环节五
学习与反思
§ 2.1 向量的加法
北师大(2019)必修2
聚焦知识目标
1.掌握向量加法的定义,会用向量加法的三角形法则和向量加法的平行四边形法则作两个向量的和向量.
2.掌握向量加法的交换律和结合律,并会用它们进行向量计算.
聚焦知识目标和数学素养
(1) 掌握向量加法及其几何意义,并会进行向量计算,提升学生的逻辑推理素养;
(2)在向量加法概念形成过程中,理解向量加法概念,培养学生的数学抽象、逻辑推理、数学运算素养;
(3)在概念教学的具体应用中,培养学生的数学建模、直观想象素养。
环节一
情境引入
情境引入
天车是大型生产车间或工地进行起重作业的重要设备.如图,物体在天车的作用下,同时进行竖直方向的宣移和水平方向的位移,
天车
实际位移可以看作竖直方向的位移与水平方向的位移的合成.
位移的合成是以,为邻边的ACBD的对角线,位移的合成遵循平行四边形法则.
环节二
向量加法概念
向量加法概念
求两个向量和的运算,称为向量的加法.
已知两个不共线的向量,,如图,在平面内任取一点A,作有向线段=,以有向线段和 为邻边作平行四边形ABCD,则有向线段表示的向量即为向量,的和,记作+.
A
B
D
加法
C
向量加法概念
求两个向量和的运算,称为向量的加法.
已知两个不共线的向量,,如图,在平面内任取一点A,作有向线段=,以有向线段和 为邻边作平行四边形ABCD,则有向线段表示的向量即为向量,的和,记作+.
A
B
D
平行四边形法则
这种求两个向量和的作图方法称为向量加法的平行四边形法则.
C
向量加法概念
显然,如图,作有向线段 以有向线段 ,的终点为起点,作有向线段连接A,C得到有向线段,也可以表示向量与的和
A
B
D
三角形法则
这种求两个向量和的作图方法称为向量加法的三角形法则.
C
向量加法概念
若,共线,表示了两个共线向量求和的情形.
特殊情形加法
同向加法
+
+
反向加法
向量加法概念
若,共线,表示了两个共线向量求和的情形.
特殊情形加法
也就是说,若两个共线向量方向相同,则它们的和向量方向与原方向一致,大小为两个向量大小之和;若两个共线向量方向相反且大小不相等,则它们的和向量方向向与较大向量的方向一致,大小是两个向量大小差的绝对值
向量加法概念
若,共线,表示了两个共线向量求和的情形.
特殊情形加法
由向量加法的定义可知,互为相反向量的两个向量的和为零向量,即 +(-)=(- )+ =.
环节三
向量加法法则应用
向量的加法法则应用
【例1】 (1)如图①,用向量加法的三角形法则作出a+b;
(2)如图②,用向量加法的平行四边形法则作出a+b.
作图题
向量的加法法则应用
作图题
解后心得
用三角形法则求和向量,关键是抓住“首尾相连”,和向量是第一个向量的起点指向第二个向量的终点,平行四边形法则注意“共起点”.且两种方法中,第一个向量的起点可任意选取,可在某一个向量上,也可在其它位置.两向量共线时,三角形法则仍适用,平行四边形法则不适用.
向量的加法法则应用
练习
向量的加法法则应用
应用题
例2.轮船从A港沿北偏东60°方向行驶了40n mile到达B处,再由B处沿正北方向行驶40n mile到达C处.求此时轮船与A港的相对位置.
解如图,、分别表示轮船的两次位移,则表示轮船的合位移
设正东方向所在直线为AE,过点B作AE的垂线,垂足为点D.
Rt△ADB中,△ADB=90°,△DAB=30° 0nmile.所以 ·sin∠DAB=40·sin30°=20(n mile),
向量的加法法则应用
应用题
例2.轮船从A港沿北偏东60°方向行驶了40n mile到达B处,再由B处沿正北方向行驶40n mile到达C处.求此时轮船与A港的相对位置.
解如图,、分别表示轮船的两次位移,则表示轮船的合位移
设正东方向所在直线为AE,过点B作AE的垂线,垂足为点D.
cos∠DAB=40·cos30°
在Rt△ADC中,△ADC=90°. (n mile),由勾股定理得
环节四
向量加法的运算律
向量加法的运算律
我们熟知,数的加法满足结合律和交换律,即对任意α,β,γ∈R,(a+β)+γ=a+(β+γ),
α+β=β+α.
那么向量的加法运算满足哪些运算律呢?
向量的加法也满足结合律和交换律,即
( +)+ = +( +),+ =+.
向量加法的运算律
先证明向量,. 的加法满足结合律.
证明结合律
向量加法的运算律
再证明向量,的加法满足交换律
证明交换律
向量加法的运算律
例3.已知向量,,如图,求作++.
应用运算律
在平面内任取一点O,作 =, =, =,如图,则由向量加法的三角形法则,得
解后心得
应用运算律
用三角形法则作两向量的和时,要注意两向量“首尾相接”;用平行四边形法则作两向量的和时,要注意保证两向量有公共起点.
2.求作共线向量或多个向量的和向量时,应首选三角形法则,注意和向量的方向是从起始向量的起点指向末尾向量的终点.
向量加法的运算律
怎样求作多个向量的和
思考
(1)由于向量的加法既满足交换律,又满足结合律,因此多个向量的加法运算即可按任意的次序与组合来求作.
(2)向量的多边形法则:
①在平面内任取一点,以此点为起点作第一个向量;
②以第一个向量的终点为起点作第二个向量;
③依次类推,最后以第n-1个向量的终点为起点作第n个向量;
④则以第一个向量的起点为起点,以第n个向量的终点为终点的向量,就是这n个向量的和.
环节五
学习与反思
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
