7.2 万有引力定律 课件(19张PPT)
文档属性
| 名称 | 7.2 万有引力定律 课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-10 17:40:08 | ||
图片预览




文档简介
(共19张PPT)
7.2万有引力定律
_____________________________________________
Newton’s Law of Universal Gravitation
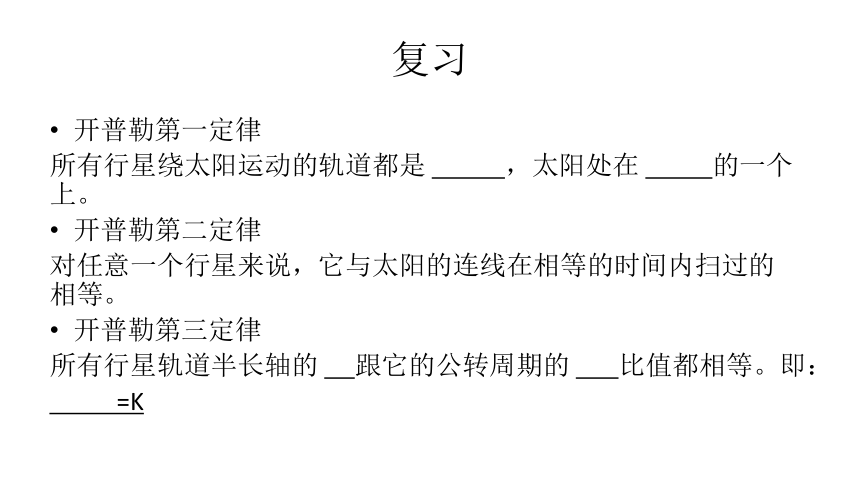
复习
开普勒第一定律
所有行星绕太阳运动的轨道都是 ,太阳处在 的一个 上。
开普勒第二定律
对任意一个行星来说,它与太阳的连线在相等的时间内扫过的 相等。
开普勒第三定律
所有行星轨道半长轴的 跟它的公转周期的 比值都相等。即:
=K
什么力来维持行星绕太阳的运动呢?
为了简化问题,我们把行星的轨道当做圆来处理(今后也如此!)
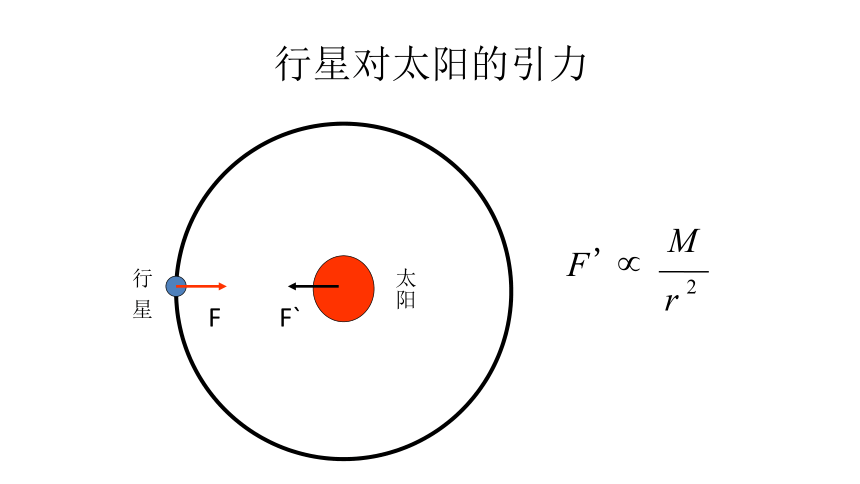
太阳对行星的引力
太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。
F
F`
行 星
太阳
行星对太阳的引力
2
,
r
M
F
一、行星与太阳间的引力
G为比例系数,与太阳、行星的质量无关
方向:沿着太阳和行星的连线
2
,
r
M
F
行星绕太阳运动
月亮绕地球运动
苹果落地……
牛顿大胆的猜想:
这些力是同一种性质的力,并且都遵从与距离平方成反比的关系。
二、月-地检验
如何检验月球与地球之间的
吸引力也满足此关系?
<1>根据向心加速度公式计算an:
an=4π2r/T2
=2.71×10-3m/s2
<2>根据F引= GMm/r2计算a:
即
地球表面:
对于月球:
结论:……
即
an=a
二、月-地检验
三、万有引力定律
自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量成正比,跟它们的距离的二次方成反比.
G为引力常量
如何得到G的数值?
扭秤实验(放大法)
引力常量G的测量
卡文迪许实验室
G为引力常量: G = 6.67×10-11 N·m2/kg2
卡文迪许实验室
共产生了29位诺贝尔奖得主
参考资料:wikipedia(维基百科)
@Brussels, 1927 in October
三、万有引力定律
自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量成正比,跟它们的距离的二次方成反比.
G为引力常量: G = 6.67×10-11 N m2/kg2
若你和同桌紧紧拥抱在一起,那你们之间的引力如何?
r→0 ,F→无穷大(impossible!!!)
例:估算你和你同桌之间的万有引力?
(建模:两位同学的质量均约为 50 kg,相距 0.5 m)
6.67×10-7 N
三、万有引力定律
自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量成正比,跟它们的距离的二次方成反比.
G为引力常量: G = 6.67×10-11 N m2/kg2
适用条件:r 是质点与质点之间的距离
(或者是均匀球体球心之间的距离)
r1
r
r2
重点: 的应用计算
例: 作业本P39 6
书P41 2、3
例:作业本P40 9
即
在地上:
难点:万有引力的效果
在天上:
例:作业本P39 4
7.2万有引力定律
_____________________________________________
Newton’s Law of Universal Gravitation
复习
开普勒第一定律
所有行星绕太阳运动的轨道都是 ,太阳处在 的一个 上。
开普勒第二定律
对任意一个行星来说,它与太阳的连线在相等的时间内扫过的 相等。
开普勒第三定律
所有行星轨道半长轴的 跟它的公转周期的 比值都相等。即:
=K
什么力来维持行星绕太阳的运动呢?
为了简化问题,我们把行星的轨道当做圆来处理(今后也如此!)
太阳对行星的引力
太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。
F
F`
行 星
太阳
行星对太阳的引力
2
,
r
M
F
一、行星与太阳间的引力
G为比例系数,与太阳、行星的质量无关
方向:沿着太阳和行星的连线
2
,
r
M
F
行星绕太阳运动
月亮绕地球运动
苹果落地……
牛顿大胆的猜想:
这些力是同一种性质的力,并且都遵从与距离平方成反比的关系。
二、月-地检验
如何检验月球与地球之间的
吸引力也满足此关系?
<1>根据向心加速度公式计算an:
an=4π2r/T2
=2.71×10-3m/s2
<2>根据F引= GMm/r2计算a:
即
地球表面:
对于月球:
结论:……
即
an=a
二、月-地检验
三、万有引力定律
自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量成正比,跟它们的距离的二次方成反比.
G为引力常量
如何得到G的数值?
扭秤实验(放大法)
引力常量G的测量
卡文迪许实验室
G为引力常量: G = 6.67×10-11 N·m2/kg2
卡文迪许实验室
共产生了29位诺贝尔奖得主
参考资料:wikipedia(维基百科)
@Brussels, 1927 in October
三、万有引力定律
自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量成正比,跟它们的距离的二次方成反比.
G为引力常量: G = 6.67×10-11 N m2/kg2
若你和同桌紧紧拥抱在一起,那你们之间的引力如何?
r→0 ,F→无穷大(impossible!!!)
例:估算你和你同桌之间的万有引力?
(建模:两位同学的质量均约为 50 kg,相距 0.5 m)
6.67×10-7 N
三、万有引力定律
自然界中任何两个物体都是互相吸引的,引力的大小跟这两个物体的质量成正比,跟它们的距离的二次方成反比.
G为引力常量: G = 6.67×10-11 N m2/kg2
适用条件:r 是质点与质点之间的距离
(或者是均匀球体球心之间的距离)
r1
r
r2
重点: 的应用计算
例: 作业本P39 6
书P41 2、3
例:作业本P40 9
即
在地上:
难点:万有引力的效果
在天上:
例:作业本P39 4
