2021年人教版八年级数学上册13.2第2课时 用坐标表示轴对称教学课件(27张)
文档属性
| 名称 | 2021年人教版八年级数学上册13.2第2课时 用坐标表示轴对称教学课件(27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
第十三章 轴对称
13.2 用坐标表示轴对称
人教版 数学 八年级 上册
学习目标
探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.(重点)
能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.( 重点)
能根据坐标系中轴对称点的坐标特点解决简单的问题.(难点)
导入新课
问题引入
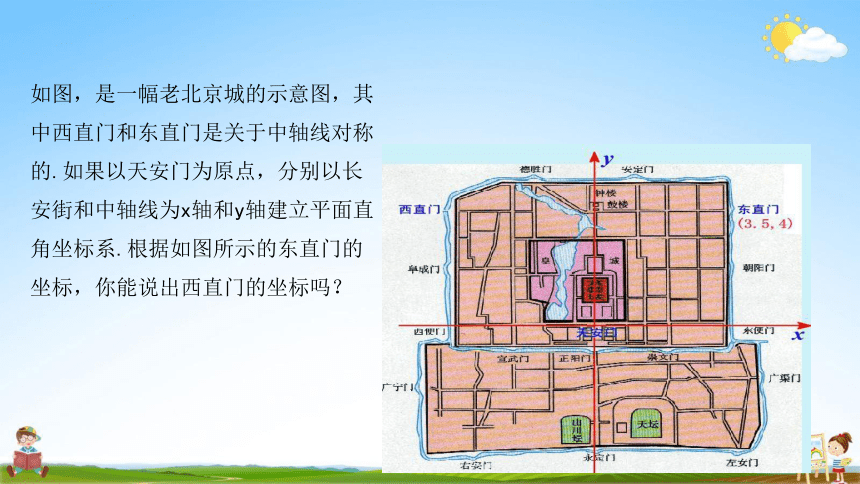
一位外国游客在天安门广场询问小明西直门的位置,
但他只知道东直门的位置,聪明的小明想了想,就准 确的告诉了他,你能猜到小明是怎么做的吗?
如图,是一幅老北京城的示意图,其 中西直门和东直门是关于中轴线对称 的.如果以天安门为原点,分别以长 安街和中轴线为x轴和y轴建立平面直 角坐标系.根据如图所示的东直门的 坐标,你能说出西直门的坐标吗?
讲授新课
用坐标表示轴对称
一
互动探究
问题1:已知点A和一条直线MN,你能画出这个点关于已知直 线的对称点吗
A
A′
M
N
O
(2)延长AO至A′,使
OA′=AO.
∴A′就是点A关于直线MN
的对称点.
(1)过点A作AO⊥MN, 垂足为点O,
x
y
O
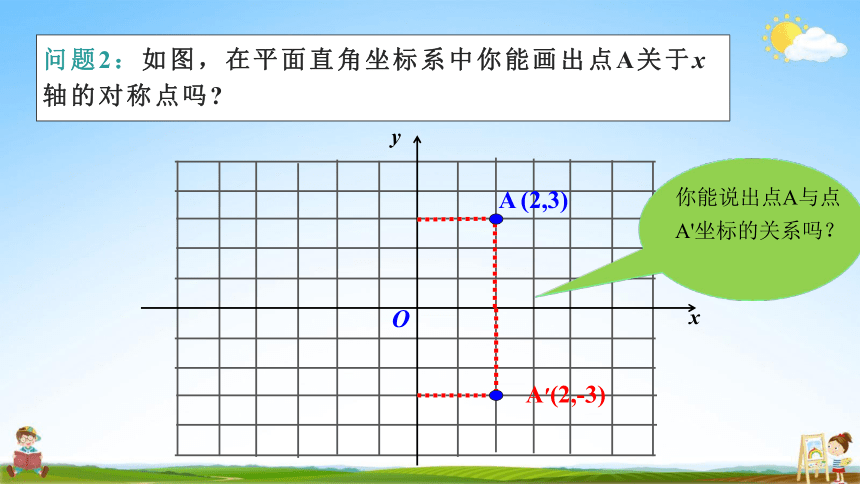
问题2 : 如图, 在平面直角坐标系中你能画出点A关于x 轴的对称点吗
A (2,3)
A′(2,-3)
你能说出点A与点
A'坐标的关系吗?
x
y
O
做一做: 在平面直角坐标系中画出下列各点关于x 轴的对称点.
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
(x , y)
关于 x 轴对称
( x , -y)
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
练一练:
1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为 (-_5 ,_-_6 ) .
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a= -2 ,
b = 5 .
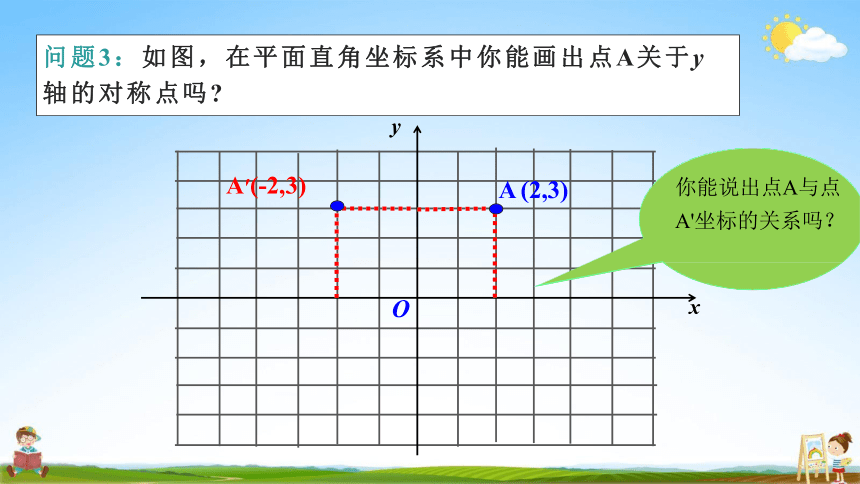
问题3 : 如图, 在平面直角坐标系中你能画出点A关于y 轴的对称点吗
x
y
O
A (2,3)
A′(-2,3)
你能说出点A与点
A'坐标的关系吗?
x
y
O
做一做: 在平面直角坐标系中画出下列各点关于y 轴的
对称点.
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
(x , y)
关于 y轴对称
( -x , y)
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(简称:纵轴纵相等)
练一练:
1.点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为
.
(5 , 6 )
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a= 2 ,
b = -_5 .
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),
C(-2,5),D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
A
B
D
A ′
B ′
C C ′
D ′
A ′
B ′
D ′
C ′
O
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对称点 的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
知识要点
在坐标系中作已知图形的对称图形
(一找二描三连)
针对训练:
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),
B(2,4),C(3,-1).
试在平面直角坐标系中,标出A、B、C三点;
若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写 出A'、B'、C'的坐标.
解:如图所示:
x
y
O
A (0,4)
B (2,4)
C (3,-1)
A' (0,-4)
B' (2,-4)
C' (3,1)
例2 已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值; (2)若A、B关于y轴对称,求(4a+b)2016的值. 解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0, 解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b, 解得a=-1,b=3,
∴(4a+b)2016=1.
解决此类题可根据关于x 轴、y轴对称的点的特征 列方程(组)求解.
例3 已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a
的取值范围.
解:依题意得P点在第四象限,
a+1>0
2a 1<0.
解得
1
2
1< a<
即a的取值范围是
1
2
1< a<
方法总结:解决此类题,一般先写出对称点的坐标或判断已知所
在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
当堂练习
1.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于
B.x轴对称
D.直线y=x对称
A.(-4,-2) C.(-2,2)
B.(2,2) D.(2,-2)
2.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得 到点B,则点B关于x轴的对称点C的坐标是( D )
( B )
A.y轴对称
C.原点对称
3.设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M关于y轴
)
的对称点的坐标是(
A.(2,3) C.(-3,2)
B.(-2,3) D.(-3,-2)
A
4.如图,在平面直角坐标系中,点P(-1,2)关于直线x=1的对称点 的坐标为( C )
A.(1,2) B.(2,2) C.(3,2) D.(4,2)
5.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a= 2 , b= 4 .
若点P与点P′关于y轴对称,则a= 6
,b= -20 .
6.若|a-2|+(b-5)2=0,则点P (a,b)关于x轴对称的点的坐标为
.
(_2_,-_5_)
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴的对称点分别为
A ′(3,5),B ′(4,1),C ′(1,3).
依次连接A ′ B ′,B ′ C ′,C ′ A ′,
就得到△ABC关于y轴对称的
△A ′ B ′ C ′.
4
3
2
1
5
-1
-2
-3
-4
1 2 3 4 5
-4 -3 -2 -1 O
A
C
B
B ′
A′
C ′
x
7.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3), 作出△ABC关于y轴对称的图形.
y
8.已知点A(2a+b,-4),B(3,a-2b)关于x轴对称,求
点C(a,b)在第几象限?
解:∵点A(2a+b,-4),B(3,a-2b)关于x轴对称,
∴2a+b=3,a-2b=4, 解得a=2,b=-1.
∴点C(2,-1)在第四象限.
拓展提升
9.在平面直角坐标系中,规定把一个正方形先 沿着x轴翻折,再向右平移2个单位称为1次变 换.如图,已知正方形ABCD的顶点A、B的坐 标分别是(-1,-1)、(-3,-1),把正方形 ABCD经过连续7次这样的变换得到正方形 A′B′C′D′,求B的对应点B′的坐标.
解:∵正方形ABCD,点A、B的坐标分别是(-1,-1)、(-3,-1),
∴根据题意,得第1次变换后的点B的对应点的坐标为(-3+2,1),即(-1,1), 第2次变换后的点B的对应点的坐标为(-1+2,-1),即(1,-1),
第3次变换后的点B的对应点的坐标为(1+2,1),即(3,1), 第n次变换后的点B的对应点的为:当n为奇数时为(2n-3,1), 当n为偶数时为(2n-3,-1),
∴把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′, 则点B的对应点B′的坐标是(11,1).
课堂小结
用坐标表示轴 对 称
关于坐标轴对称的点的 坐 标 特 征
在坐标系中作已 知图形的对称图 形
关于x轴对称,横同纵反; 关于y轴对称,横反纵同
关键要明确点关于x轴、y轴对称点的坐 标变化规律,然后正确描出对称点的位 置
谢谢观看
Thank You
第十三章 轴对称
13.2 用坐标表示轴对称
人教版 数学 八年级 上册
学习目标
探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.(重点)
能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.( 重点)
能根据坐标系中轴对称点的坐标特点解决简单的问题.(难点)
导入新课
问题引入
一位外国游客在天安门广场询问小明西直门的位置,
但他只知道东直门的位置,聪明的小明想了想,就准 确的告诉了他,你能猜到小明是怎么做的吗?
如图,是一幅老北京城的示意图,其 中西直门和东直门是关于中轴线对称 的.如果以天安门为原点,分别以长 安街和中轴线为x轴和y轴建立平面直 角坐标系.根据如图所示的东直门的 坐标,你能说出西直门的坐标吗?
讲授新课
用坐标表示轴对称
一
互动探究
问题1:已知点A和一条直线MN,你能画出这个点关于已知直 线的对称点吗
A
A′
M
N
O
(2)延长AO至A′,使
OA′=AO.
∴A′就是点A关于直线MN
的对称点.
(1)过点A作AO⊥MN, 垂足为点O,
x
y
O
问题2 : 如图, 在平面直角坐标系中你能画出点A关于x 轴的对称点吗
A (2,3)
A′(2,-3)
你能说出点A与点
A'坐标的关系吗?
x
y
O
做一做: 在平面直角坐标系中画出下列各点关于x 轴的对称点.
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
(x , y)
关于 x 轴对称
( x , -y)
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
练一练:
1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为 (-_5 ,_-_6 ) .
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a= -2 ,
b = 5 .
问题3 : 如图, 在平面直角坐标系中你能画出点A关于y 轴的对称点吗
x
y
O
A (2,3)
A′(-2,3)
你能说出点A与点
A'坐标的关系吗?
x
y
O
做一做: 在平面直角坐标系中画出下列各点关于y 轴的
对称点.
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
(x , y)
关于 y轴对称
( -x , y)
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(简称:纵轴纵相等)
练一练:
1.点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为
.
(5 , 6 )
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a= 2 ,
b = -_5 .
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),
C(-2,5),D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
A
B
D
A ′
B ′
C C ′
D ′
A ′
B ′
D ′
C ′
O
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对称点 的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
知识要点
在坐标系中作已知图形的对称图形
(一找二描三连)
针对训练:
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),
B(2,4),C(3,-1).
试在平面直角坐标系中,标出A、B、C三点;
若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写 出A'、B'、C'的坐标.
解:如图所示:
x
y
O
A (0,4)
B (2,4)
C (3,-1)
A' (0,-4)
B' (2,-4)
C' (3,1)
例2 已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值; (2)若A、B关于y轴对称,求(4a+b)2016的值. 解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0, 解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b, 解得a=-1,b=3,
∴(4a+b)2016=1.
解决此类题可根据关于x 轴、y轴对称的点的特征 列方程(组)求解.
例3 已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a
的取值范围.
解:依题意得P点在第四象限,
a+1>0
2a 1<0.
解得
1
2
1< a<
即a的取值范围是
1
2
1< a<
方法总结:解决此类题,一般先写出对称点的坐标或判断已知所
在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
当堂练习
1.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于
B.x轴对称
D.直线y=x对称
A.(-4,-2) C.(-2,2)
B.(2,2) D.(2,-2)
2.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得 到点B,则点B关于x轴的对称点C的坐标是( D )
( B )
A.y轴对称
C.原点对称
3.设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M关于y轴
)
的对称点的坐标是(
A.(2,3) C.(-3,2)
B.(-2,3) D.(-3,-2)
A
4.如图,在平面直角坐标系中,点P(-1,2)关于直线x=1的对称点 的坐标为( C )
A.(1,2) B.(2,2) C.(3,2) D.(4,2)
5.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a= 2 , b= 4 .
若点P与点P′关于y轴对称,则a= 6
,b= -20 .
6.若|a-2|+(b-5)2=0,则点P (a,b)关于x轴对称的点的坐标为
.
(_2_,-_5_)
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴的对称点分别为
A ′(3,5),B ′(4,1),C ′(1,3).
依次连接A ′ B ′,B ′ C ′,C ′ A ′,
就得到△ABC关于y轴对称的
△A ′ B ′ C ′.
4
3
2
1
5
-1
-2
-3
-4
1 2 3 4 5
-4 -3 -2 -1 O
A
C
B
B ′
A′
C ′
x
7.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3), 作出△ABC关于y轴对称的图形.
y
8.已知点A(2a+b,-4),B(3,a-2b)关于x轴对称,求
点C(a,b)在第几象限?
解:∵点A(2a+b,-4),B(3,a-2b)关于x轴对称,
∴2a+b=3,a-2b=4, 解得a=2,b=-1.
∴点C(2,-1)在第四象限.
拓展提升
9.在平面直角坐标系中,规定把一个正方形先 沿着x轴翻折,再向右平移2个单位称为1次变 换.如图,已知正方形ABCD的顶点A、B的坐 标分别是(-1,-1)、(-3,-1),把正方形 ABCD经过连续7次这样的变换得到正方形 A′B′C′D′,求B的对应点B′的坐标.
解:∵正方形ABCD,点A、B的坐标分别是(-1,-1)、(-3,-1),
∴根据题意,得第1次变换后的点B的对应点的坐标为(-3+2,1),即(-1,1), 第2次变换后的点B的对应点的坐标为(-1+2,-1),即(1,-1),
第3次变换后的点B的对应点的坐标为(1+2,1),即(3,1), 第n次变换后的点B的对应点的为:当n为奇数时为(2n-3,1), 当n为偶数时为(2n-3,-1),
∴把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′, 则点B的对应点B′的坐标是(11,1).
课堂小结
用坐标表示轴 对 称
关于坐标轴对称的点的 坐 标 特 征
在坐标系中作已 知图形的对称图 形
关于x轴对称,横同纵反; 关于y轴对称,横反纵同
关键要明确点关于x轴、y轴对称点的坐 标变化规律,然后正确描出对称点的位 置
谢谢观看
Thank You
