2021年人教版八年级数学上册13.4课题学习 最短路径问题教学课件(32张)
文档属性
| 名称 | 2021年人教版八年级数学上册13.4课题学习 最短路径问题教学课件(32张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 23:41:19 | ||
图片预览







文档简介
(共32张PPT)
第十三章 轴对称
13.4 课题学习 最短路径问题
人教版 数学 八年级 上册
学习目标
能利用轴对称解决简单的最短路径问题.(难点)
体会图形的变化在解决最值问题中的作用,感悟转化思想.(重点)
导入新课
复习引入
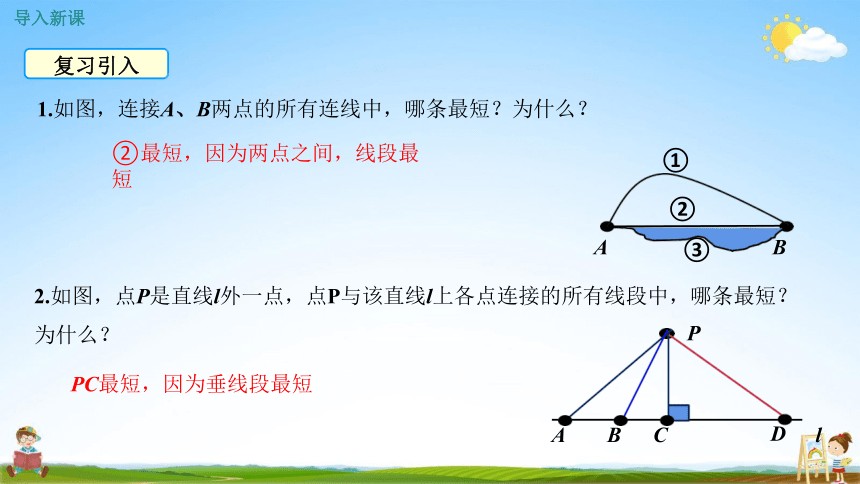
1.如图,连接A、B两点的所有连线中,哪条最短?为什么?
A B
①
②
③
②最短,因为两点之间,线段最短
2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?
为什么?
P
l
A B C
D
PC最短,因为垂线段最短
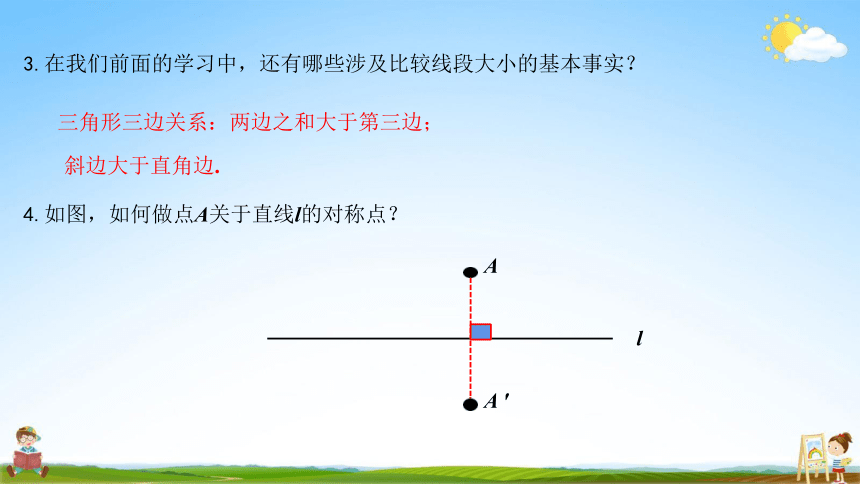
在我们前面的学习中,还有哪些涉及比较线段大小的基本事实?
三角形三边关系:两边之和大于第三边; 斜边大于直角边.
如图,如何做点A关于直线l的对称点?
A
l
A ′
讲授新课
牧人饮马问题
一
“两点的所有连线中,线段最短”“连接直线外一点与直线上各点的所有 线段中,垂线段最短”等的问题,我们称之为最短路径问题.
现实生活中经常涉及到选择最短路径问题,本节将利用数学知识探究数学 史的著名的“牧马人饮马问题”及“造桥选址问题”.
A
B
①
②
③
P
l
A B C
D
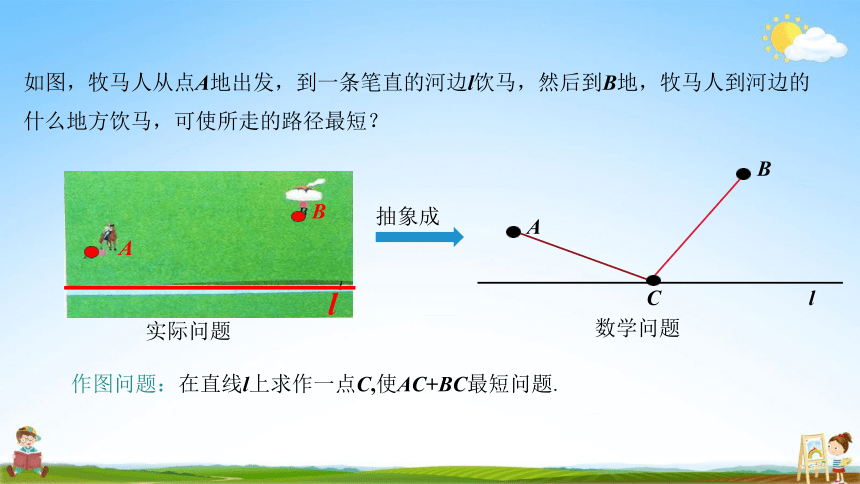
如图,牧马人从点A地出发,到一条笔直的河边l饮马,然后到B地,牧马人到河边的 什么地方饮马,可使所走的路径最短?
抽象成
A
B
l
C
数学问题
作图问题:在直线l上求作一点C,使AC+BC最短问题.
实际问题
A
B
l
问题1 现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点, 使得这个点到点A,点B的距离的和最短?
A
l
B
C
根据是“两点之间,线段最短”,可知这 个交点即为所求.
连接AB,与直线l相交于一点C.
问题2 如果点A,B分别是直线l同侧的两个点,又应该如何解决?
想一想:对于问题2,如何将点B“移”到l 的另一侧B′ 处,满足直线l 上的任意一点C,都保持CB 与CB′的长 度相等?
A
B
l
利用轴对称,作出点B关于直线l的对称点B′.
方法揭晓
作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C. 则点C 即为所求.
A
B
l
B ′
C
问题3 你能用所学的知识证明AC +BC最短吗?
证明:如图,在直线l 上任取一点C′(与点C 不重合),连 接AC′,BC′,B′C′.由轴对称的性质可知,
BC =B′C,BC′=B′C′.
∴ AC +BC= AC +B′C = AB′,
∴ AC′+BC′= AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′. 即 AC +BC 最短.
A
B
l
B ′
C
C ′
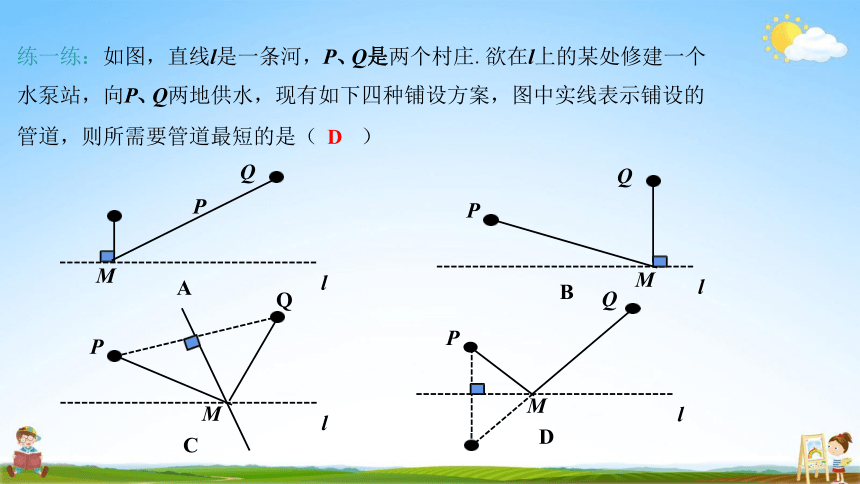
练一练:如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个 水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的
l
A
M
P
Q
l
B
M
P
Q
l
C
M
P
Q
l
M
D
管道,则所需要管道最短的是( D )
Q
P
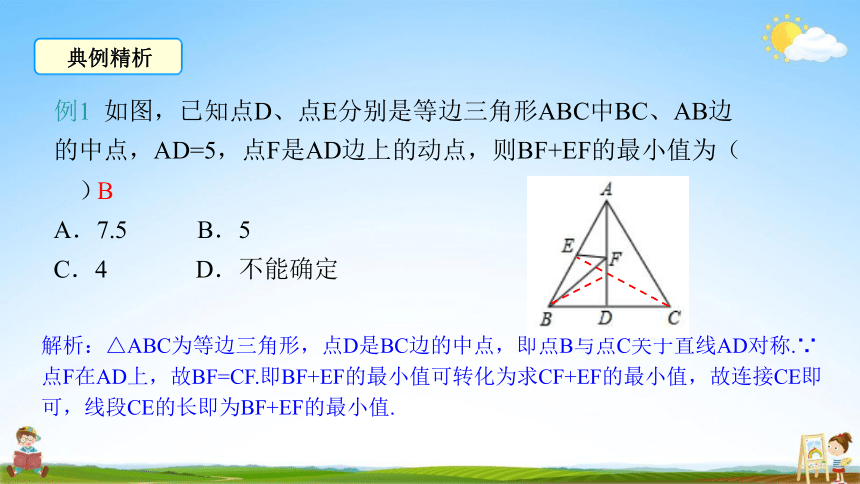
A.7.5
C.4
B.5
D.不能确定
典例精析
解析:△ABC为等边三角形,点D是BC边的中点,即点B与点C关于直线AD对称.∵ 点F在AD上,故BF=CF.即BF+EF的最小值可转化为求CF+EF的最小值,故连接CE即 可,线段CE的长即为BF+EF的最小值.
例1 如图,已知点D、点E分别是等边三角形ABC中BC、AB边 的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为(
)B
方法总结:此类求线段和的最小值问题,找准对称点是关键,而
后将求线段长的和转化为求某一线段的长,而再根据已知条件求 解.
例2 如图,在直角坐标系中,点A,B的坐标分别为(1,
4)和(3,0),点C是y轴上的一个动点,且A,B,C
三点不在同一条直线上,当△ABC的周长最小时点C的
坐 标 是 ( A.(0,3) C.(0,1)
B.(0,2) D.(0,0)
解析:作B点关于y轴对称点B′,连接AB′,交y轴于点C′, 此时△ABC的周长最小,然后依据点A与点B′的坐标可 得到BE、AE的长,然后证明△B′C′O为等腰直角三角形 即可.
A)
B′
C′
E
方法总结:求三角形周长的最小值,先确定动点所在的直线和固
定点,而后作某一固定点关于动点所在直线的对称点,而后将其 与另一固定点连线,连线与动点所在直线的交点即为三角形周长 最小时动点的位置.
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从
A到B的路径AMNB最短(假定河的两岸是平行的直线,桥要与河垂直)?
B
A
A
B
N
M
造桥选址问题
二
B
●
N
M
N
M
折
移
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN, 那么怎样确定什么情况下最短呢?
A
我们能否在不改变AM+MN+BN的前提下把桥转化到一侧呢?什么图 形变换能帮助我们呢?
思维火花
各抒己见
1.把A平移到岸边.
2.把B平移到岸边.
3.把桥平移到和A相连.
4.把桥平移到和B相连.
B
A
M
N
A
M
N
A'
B' B
1.把A平移到岸边.
AM+MN+BN长度改变了
2.把B平移到岸边.
AM+MN+BN长度改变了
3.把桥平移到和A相连.
AM+MN+BN长度
有没有改变呢?
A
M
N
B
4.把桥平移到和B相连.
问题解决
A
A1
M
N
1 1
如图,平移A到A ,使AA 等于河宽,连接A1B
交河岸于N作桥MN,此时路径AM+MN+BN最 短.
N1
B
M1
理由:另任作桥M1N1,连接AM1,BN1,A1N1.
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,
而 AM1+M1N1+BN1 转 化 为 AA1+A1N1+BN1. 在△A1N1B中,因为A1N1+BN1>A1B.
因此AM1+M1N1+BN1> AM+MN+BN.
A·
B
M
N
E
C
D
证明:由平移的性质,得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,所 以A到B的路径长为AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC,CD,DB,CE,则A到B的路径长为
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB >AM+MN+BN,
所以桥的位置建在MN处,A到B的路径最短.
方法归纳
解决最短路径问题的方法
在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为 已解决的问题,从而作出最短路径的选择.
当堂练习
1.如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于 直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是(
)
A.P是m上到A、B距离之和最短的 点,Q是m上到A、B距离相等的点
B.Q是m上到A、B距离之和最短的 点,P是m上到A、B距离相等的点
C.P、Q都是m上到A、B距离之和最 短的点
D.P、Q都是m上到A、B距离相等 的点
A
2.如图,∠AOB=30°,∠AOB内有一定点P,且OP=
10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周
)
B.15 D.30
长是( A A.10 C.20
3.如图,牧童在A处放马,其家在B处,A、B到河岸的距离分别为AC和BD, 且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把马牵到
河边饮水再回家,所走的最短距离是
A
C
B
D
河
10米00.
4.如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、 B的坐标分别是A(3,2),B(1,3).点P在x轴上,当PA+PB的值最小
时,在图中画出点P.
x
y
B
A
O P
B '
5.如图,襄阳古城河在CC′处直角转弯,河宽相同,从A处到B处,须经 两座桥:DD ′,EE ′(桥宽不计),设护城河以及两座桥都是东西、南北 方向的,怎样架桥可使ADD ′E ′EB的路程最短?
A
D
D ′
C
C′
E
E′
B
解:作AF⊥CD,且AF=河宽,作BG ⊥CE,且BG=河宽,连接GF,与河 岸相交于E ′,D′.作DD′,EE′即为桥.
理由:由作图法可知,AF//DD′,AF=DD′,则四边形AFD′D为平行四边形,于是
AD=FD′,
同理,BE=GE′,
由两点之间线段最短可知,GF最小.
A
D ′
C
C′
E
E′
B
F
G
D
课堂小结
原 理
线段公理和垂线段最短
牧马人饮马 问 题
解题方法
造桥选址 问 题
关键是将固定线段“桥”平移
最 短 路 径 问 题
轴对称知识+线段公理
解题方法
谢谢观看
Thank You
第十三章 轴对称
13.4 课题学习 最短路径问题
人教版 数学 八年级 上册
学习目标
能利用轴对称解决简单的最短路径问题.(难点)
体会图形的变化在解决最值问题中的作用,感悟转化思想.(重点)
导入新课
复习引入
1.如图,连接A、B两点的所有连线中,哪条最短?为什么?
A B
①
②
③
②最短,因为两点之间,线段最短
2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?
为什么?
P
l
A B C
D
PC最短,因为垂线段最短
在我们前面的学习中,还有哪些涉及比较线段大小的基本事实?
三角形三边关系:两边之和大于第三边; 斜边大于直角边.
如图,如何做点A关于直线l的对称点?
A
l
A ′
讲授新课
牧人饮马问题
一
“两点的所有连线中,线段最短”“连接直线外一点与直线上各点的所有 线段中,垂线段最短”等的问题,我们称之为最短路径问题.
现实生活中经常涉及到选择最短路径问题,本节将利用数学知识探究数学 史的著名的“牧马人饮马问题”及“造桥选址问题”.
A
B
①
②
③
P
l
A B C
D
如图,牧马人从点A地出发,到一条笔直的河边l饮马,然后到B地,牧马人到河边的 什么地方饮马,可使所走的路径最短?
抽象成
A
B
l
C
数学问题
作图问题:在直线l上求作一点C,使AC+BC最短问题.
实际问题
A
B
l
问题1 现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点, 使得这个点到点A,点B的距离的和最短?
A
l
B
C
根据是“两点之间,线段最短”,可知这 个交点即为所求.
连接AB,与直线l相交于一点C.
问题2 如果点A,B分别是直线l同侧的两个点,又应该如何解决?
想一想:对于问题2,如何将点B“移”到l 的另一侧B′ 处,满足直线l 上的任意一点C,都保持CB 与CB′的长 度相等?
A
B
l
利用轴对称,作出点B关于直线l的对称点B′.
方法揭晓
作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C. 则点C 即为所求.
A
B
l
B ′
C
问题3 你能用所学的知识证明AC +BC最短吗?
证明:如图,在直线l 上任取一点C′(与点C 不重合),连 接AC′,BC′,B′C′.由轴对称的性质可知,
BC =B′C,BC′=B′C′.
∴ AC +BC= AC +B′C = AB′,
∴ AC′+BC′= AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′. 即 AC +BC 最短.
A
B
l
B ′
C
C ′
练一练:如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个 水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的
l
A
M
P
Q
l
B
M
P
Q
l
C
M
P
Q
l
M
D
管道,则所需要管道最短的是( D )
Q
P
A.7.5
C.4
B.5
D.不能确定
典例精析
解析:△ABC为等边三角形,点D是BC边的中点,即点B与点C关于直线AD对称.∵ 点F在AD上,故BF=CF.即BF+EF的最小值可转化为求CF+EF的最小值,故连接CE即 可,线段CE的长即为BF+EF的最小值.
例1 如图,已知点D、点E分别是等边三角形ABC中BC、AB边 的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为(
)B
方法总结:此类求线段和的最小值问题,找准对称点是关键,而
后将求线段长的和转化为求某一线段的长,而再根据已知条件求 解.
例2 如图,在直角坐标系中,点A,B的坐标分别为(1,
4)和(3,0),点C是y轴上的一个动点,且A,B,C
三点不在同一条直线上,当△ABC的周长最小时点C的
坐 标 是 ( A.(0,3) C.(0,1)
B.(0,2) D.(0,0)
解析:作B点关于y轴对称点B′,连接AB′,交y轴于点C′, 此时△ABC的周长最小,然后依据点A与点B′的坐标可 得到BE、AE的长,然后证明△B′C′O为等腰直角三角形 即可.
A)
B′
C′
E
方法总结:求三角形周长的最小值,先确定动点所在的直线和固
定点,而后作某一固定点关于动点所在直线的对称点,而后将其 与另一固定点连线,连线与动点所在直线的交点即为三角形周长 最小时动点的位置.
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从
A到B的路径AMNB最短(假定河的两岸是平行的直线,桥要与河垂直)?
B
A
A
B
N
M
造桥选址问题
二
B
●
N
M
N
M
折
移
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN, 那么怎样确定什么情况下最短呢?
A
我们能否在不改变AM+MN+BN的前提下把桥转化到一侧呢?什么图 形变换能帮助我们呢?
思维火花
各抒己见
1.把A平移到岸边.
2.把B平移到岸边.
3.把桥平移到和A相连.
4.把桥平移到和B相连.
B
A
M
N
A
M
N
A'
B' B
1.把A平移到岸边.
AM+MN+BN长度改变了
2.把B平移到岸边.
AM+MN+BN长度改变了
3.把桥平移到和A相连.
AM+MN+BN长度
有没有改变呢?
A
M
N
B
4.把桥平移到和B相连.
问题解决
A
A1
M
N
1 1
如图,平移A到A ,使AA 等于河宽,连接A1B
交河岸于N作桥MN,此时路径AM+MN+BN最 短.
N1
B
M1
理由:另任作桥M1N1,连接AM1,BN1,A1N1.
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,
而 AM1+M1N1+BN1 转 化 为 AA1+A1N1+BN1. 在△A1N1B中,因为A1N1+BN1>A1B.
因此AM1+M1N1+BN1> AM+MN+BN.
A·
B
M
N
E
C
D
证明:由平移的性质,得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,所 以A到B的路径长为AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC,CD,DB,CE,则A到B的路径长为
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB >AM+MN+BN,
所以桥的位置建在MN处,A到B的路径最短.
方法归纳
解决最短路径问题的方法
在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为 已解决的问题,从而作出最短路径的选择.
当堂练习
1.如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于 直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是(
)
A.P是m上到A、B距离之和最短的 点,Q是m上到A、B距离相等的点
B.Q是m上到A、B距离之和最短的 点,P是m上到A、B距离相等的点
C.P、Q都是m上到A、B距离之和最 短的点
D.P、Q都是m上到A、B距离相等 的点
A
2.如图,∠AOB=30°,∠AOB内有一定点P,且OP=
10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周
)
B.15 D.30
长是( A A.10 C.20
3.如图,牧童在A处放马,其家在B处,A、B到河岸的距离分别为AC和BD, 且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把马牵到
河边饮水再回家,所走的最短距离是
A
C
B
D
河
10米00.
4.如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、 B的坐标分别是A(3,2),B(1,3).点P在x轴上,当PA+PB的值最小
时,在图中画出点P.
x
y
B
A
O P
B '
5.如图,襄阳古城河在CC′处直角转弯,河宽相同,从A处到B处,须经 两座桥:DD ′,EE ′(桥宽不计),设护城河以及两座桥都是东西、南北 方向的,怎样架桥可使ADD ′E ′EB的路程最短?
A
D
D ′
C
C′
E
E′
B
解:作AF⊥CD,且AF=河宽,作BG ⊥CE,且BG=河宽,连接GF,与河 岸相交于E ′,D′.作DD′,EE′即为桥.
理由:由作图法可知,AF//DD′,AF=DD′,则四边形AFD′D为平行四边形,于是
AD=FD′,
同理,BE=GE′,
由两点之间线段最短可知,GF最小.
A
D ′
C
C′
E
E′
B
F
G
D
课堂小结
原 理
线段公理和垂线段最短
牧马人饮马 问 题
解题方法
造桥选址 问 题
关键是将固定线段“桥”平移
最 短 路 径 问 题
轴对称知识+线段公理
解题方法
谢谢观看
Thank You
