2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册8.2.1一元线性回归模型 教学课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册8.2.1一元线性回归模型 教学课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
课 题:8.2.1一元线性回归模型
年 级:高二
教 材:选择性必修三 第八章第二节第1课时
版 本:人教A版(新)
一.复习回顾
收集数据
整理数据
分析数据
统计推断
研究统计问题的一般流程
简单随机抽样
分层抽样
频数分布表
频率分布直方图
茎叶图
散点图
......
众数
中位数
平均数
方差
标准差
用样本估计总体
???
单一数据
成对数据
单一数据
线性相关系数r
......
成对数据
离散型随机变量
......
连续型随机变量
(正态分布)
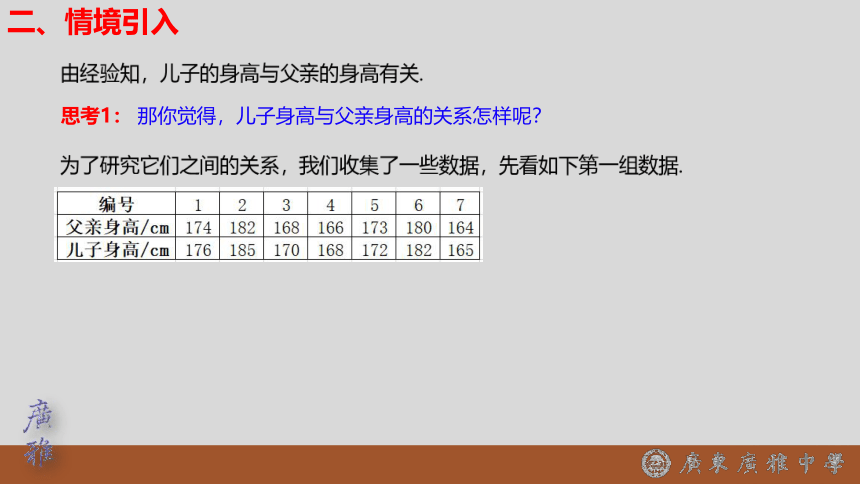
思考1:
那你觉得,儿子身高与父亲身高的关系怎样呢?
二、情境引入
二、情境引入
.
.
.
.
.
.
.
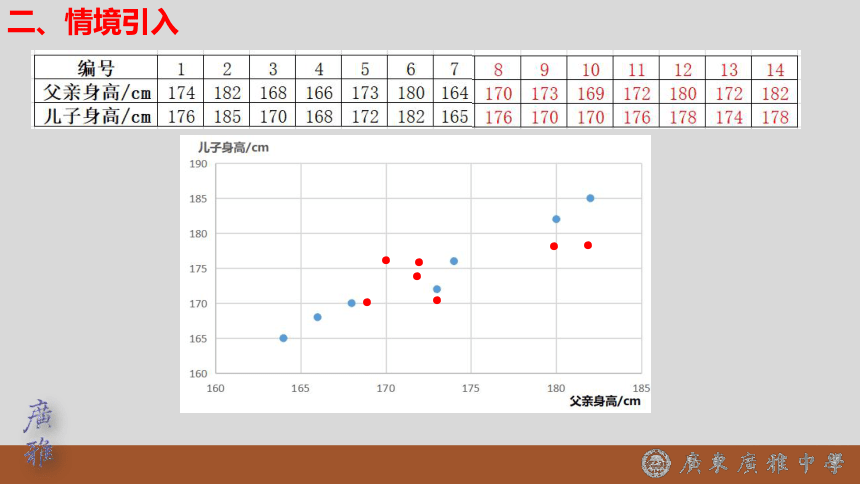
二、情境引入
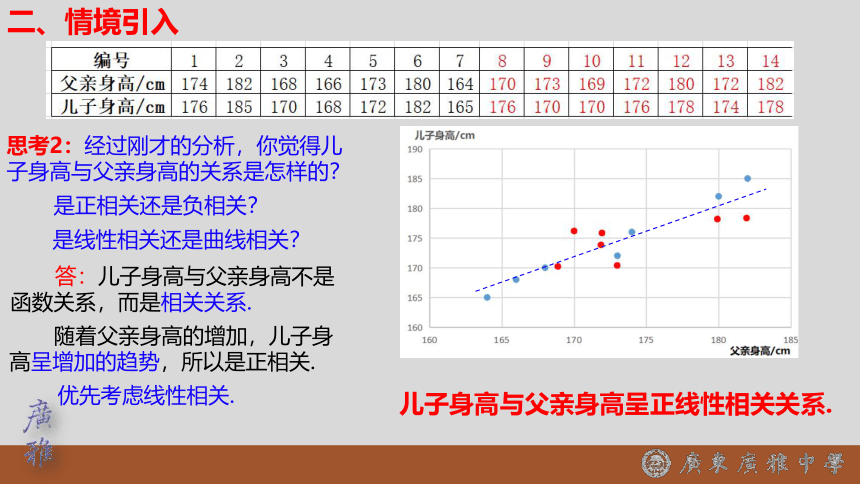
思考2:经过刚才的分析,你觉得儿子身高与父亲身高的关系是怎样的?
答:儿子身高与父亲身高不是函数关系,而是相关关系.
是正相关还是负相关?
随着父亲身高的增加,儿子身高呈增加的趋势,所以是正相关.
是线性相关还是曲线相关?
优先考虑线性相关.
儿子身高与父亲身高呈正线性相关关系.
思考3:能否进一步验证刚才的结论?
样本相关系数为:
表明儿子身高和父亲身高正线性相关,且相关程度较高.
由散点图可知,散点大致分布在一条从
左下角到右上角的直线附近,表明儿子身高和父
亲身高正线性相关.
分析:
二、情境引入
三、建立回归模型
儿子身高Y
用一次函数刻画父亲身高对儿子身高的主要影响
其它因素:母亲身高、生活环境、饮食习惯等
随机误差e (随机变量)
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
bx+a
Y=bx+a+e
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
我们称(1)式为Y关于 的一元线性回归模型.
其中,Y称为因变量或响应变量, 称为自变量
或解释变量; 为模型的未知参数 , 称为
截距参数, 称为斜率参数.
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
概念辨析4:能否进一步结合实例解释产生
模型(1)中随机误差的原因?
三、建立回归模型
四、练习巩固,加深理解
四、练习巩固,加深理解
五、课堂小结
(二)建立一元线性回归模型的步骤
(一)一元线性回归模型
(1)与函数模型的区别 (2)随机误差产生的原因及分布
定性分析
定量分析
函数关系 or 相关关系 or 没有关系?
谢谢大家!
课 题:8.2.1一元线性回归模型
年 级:高二
教 材:选择性必修三 第八章第二节第1课时
版 本:人教A版(新)
一.复习回顾
收集数据
整理数据
分析数据
统计推断
研究统计问题的一般流程
简单随机抽样
分层抽样
频数分布表
频率分布直方图
茎叶图
散点图
......
众数
中位数
平均数
方差
标准差
用样本估计总体
???
单一数据
成对数据
单一数据
线性相关系数r
......
成对数据
离散型随机变量
......
连续型随机变量
(正态分布)
思考1:
那你觉得,儿子身高与父亲身高的关系怎样呢?
二、情境引入
二、情境引入
.
.
.
.
.
.
.
二、情境引入
思考2:经过刚才的分析,你觉得儿子身高与父亲身高的关系是怎样的?
答:儿子身高与父亲身高不是函数关系,而是相关关系.
是正相关还是负相关?
随着父亲身高的增加,儿子身高呈增加的趋势,所以是正相关.
是线性相关还是曲线相关?
优先考虑线性相关.
儿子身高与父亲身高呈正线性相关关系.
思考3:能否进一步验证刚才的结论?
样本相关系数为:
表明儿子身高和父亲身高正线性相关,且相关程度较高.
由散点图可知,散点大致分布在一条从
左下角到右上角的直线附近,表明儿子身高和父
亲身高正线性相关.
分析:
二、情境引入
三、建立回归模型
儿子身高Y
用一次函数刻画父亲身高对儿子身高的主要影响
其它因素:母亲身高、生活环境、饮食习惯等
随机误差e (随机变量)
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
bx+a
Y=bx+a+e
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
我们称(1)式为Y关于 的一元线性回归模型.
其中,Y称为因变量或响应变量, 称为自变量
或解释变量; 为模型的未知参数 , 称为
截距参数, 称为斜率参数.
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
三、建立回归模型
用 表示父亲身高,Y表示儿子身高, 表示
随机误差.
假定随机误差的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
概念辨析4:能否进一步结合实例解释产生
模型(1)中随机误差的原因?
三、建立回归模型
四、练习巩固,加深理解
四、练习巩固,加深理解
五、课堂小结
(二)建立一元线性回归模型的步骤
(一)一元线性回归模型
(1)与函数模型的区别 (2)随机误差产生的原因及分布
定性分析
定量分析
函数关系 or 相关关系 or 没有关系?
谢谢大家!
