2022年浙江省中考科学一轮复习 第26课时 简单机械-杠杆(课件 60张PPT)
文档属性
| 名称 | 2022年浙江省中考科学一轮复习 第26课时 简单机械-杠杆(课件 60张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2022-01-11 20:40:43 | ||
图片预览






文档简介
(共60张PPT)
第26课时 简单机械——杠杆
●知识体系梳理
●重难考点精讲
●当堂限时训练
知识体系
固定点
动力作用线
阻力作用线
动力×动力臂=阻力×阻力臂
>
<
扳手
开瓶器
=
=
天平
定滑轮
<
>
钓鱼竿
重点梳理
区别力臂和支点到力的作用点的距离
力臂是 到 的距离,是点到线的距离;支点到力的作用点的距离是点到点的距离。
这两者,当 的方向和 垂直时,两者相等;当两者不垂直时,两者不等。
支点
力的作用线
力
杠杆
对点练习
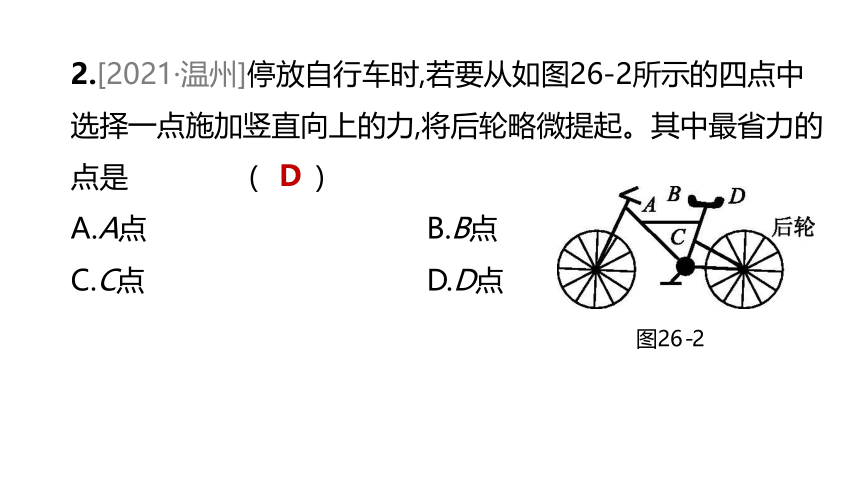
1.[2021·金华]生活中处处有科学。如图26-1所示的日常工具在使用时属于费力杠杆的是( )
图26-1
C
2.[2021·温州]停放自行车时,若要从如图26-2所示的四点中选择一点施加竖直向上的力,将后轮略微提起。其中最省力的点是 ( )
A.A点 B.B点
C.C点 D.D点
图26-2
D
3.[2017·杭州]小金将长为0.6 m、质量可忽略不计的木棒搁在肩上,棒的后端A点挂一个重40 N的物体,肩上支点O离后端A点的距离为0.2 m,他用手压住前端B点使木棒保持水平平衡,如图26-3所示。小金的质量为50 kg,则此时手压
木棒的力大小为 N,肩对木棒的支持力大小
为 N,人对地面的压力大小为 N。
(g取10 N/kg)
图26-3
20
60
540
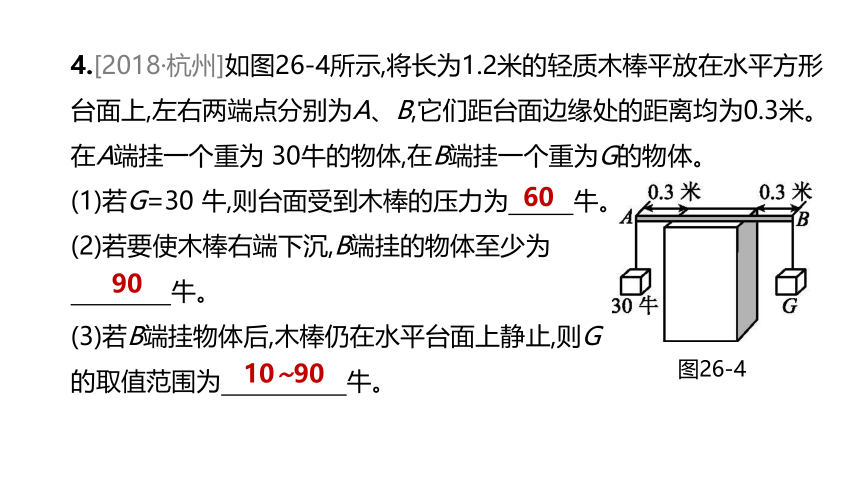
4.[2018·杭州]如图26-4所示,将长为1.2米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为 30牛的物体,在B端挂一个重为G的物体。
(1)若G=30 牛,则台面受到木棒的压力为 牛。
(2)若要使木棒右端下沉,B端挂的物体至少为
牛。
(3)若B端挂物体后,木棒仍在水平台面上静止,则G
的取值范围为 牛。
图26-4
60
90
10~90
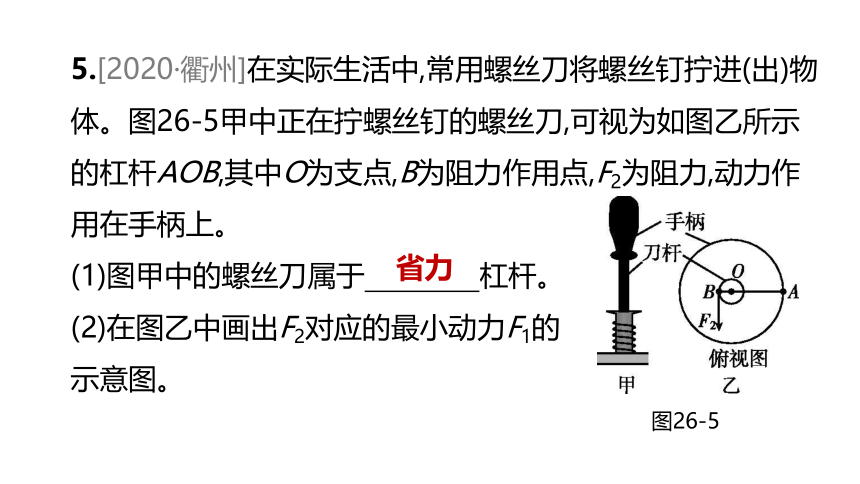
5.[2020·衢州]在实际生活中,常用螺丝刀将螺丝钉拧进(出)物体。图26-5甲中正在拧螺丝钉的螺丝刀,可视为如图乙所示的杠杆AOB,其中O为支点,B为阻力作用点,F2为阻力,动力作用在手柄上。
(1)图甲中的螺丝刀属于 杠杆。
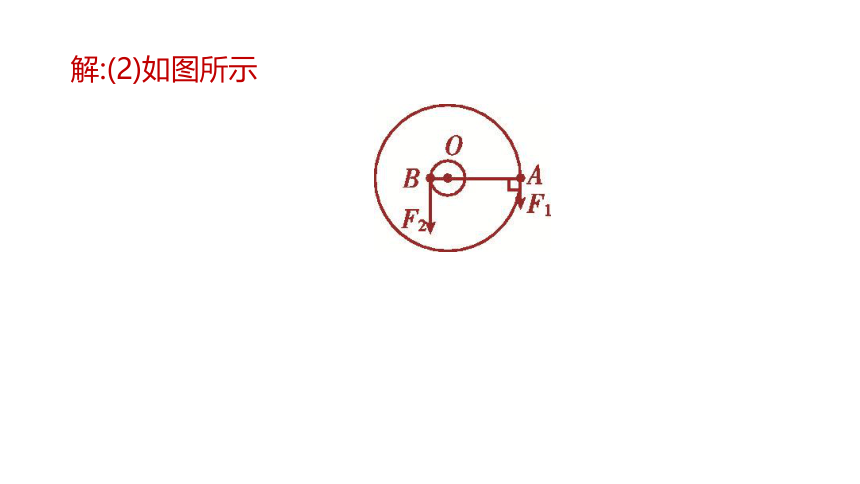
(2)在图乙中画出F2对应的最小动力F1的
示意图。
图26-5
省力
解:(2)如图所示
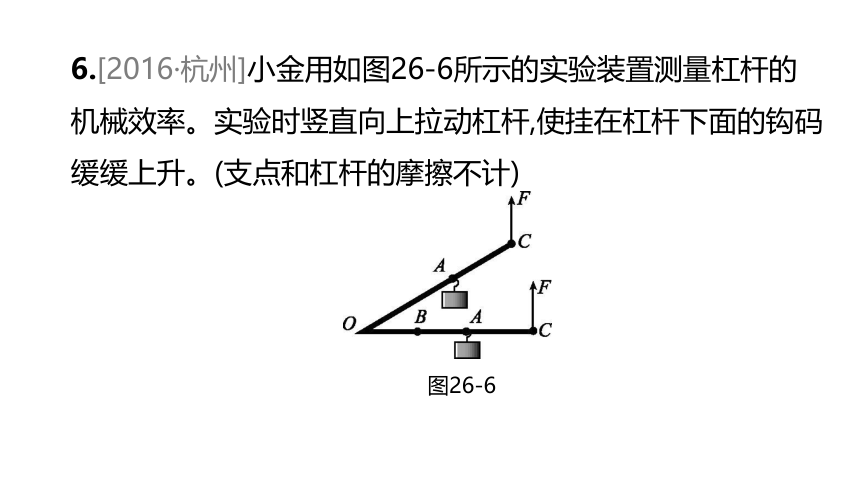
6.[2016·杭州]小金用如图26-6所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦不计)
图26-6
(1)重为5 N的钩码挂在A点时,人的拉力F始终为4 N。钩码上升0.3 m时,动力作用点C上升0.5 m,此时机械效率η1为多大
(2)小金为了进一步探究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5 m。问:与第一次相比,人的拉力F将________ (选填“变大”“变小”或“不变”)。比较此时的机械效率η2与η1的大小,并用学过的知识给以推导。
(1)重为5 N的钩码挂在A点时,人的拉力F始终为4 N。钩码上升0.3 m时,动力作用点C上升0.5 m,此时机械效率η1为多大
图26-6
解:(1)η1=×100%=×100%
=×100%=75%。
(2)小金为了进一步探究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5 m。问:与第一次相比,人的拉力F将________ (选填“变大”“变小”或“不变”)。比较此时的机械效率η2与η1的大小,并用学过的知识给以推导。
图26-6
变小
推导过程:第二次提升时,杠杆动力作用点升高的高度不变,因此克服杠杆自重所做的额外功不变。而被提升的钩码由于靠近支点,因此钩码升高的高度减小,有用功减小。机械效率
η=×100%=×100%=×100%,
而W有用27.[2015·杭州]如图26-7所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)画出θ=60°时拉力F的力臂l,并计算力臂的
大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化 并推导拉力F与角度θ的关系式。
图26-7
7.[2015·杭州]如图26-7所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)画出θ=60°时拉力F的力臂l,并计算力臂的
大小。
图26-7
解:(1)如图所示
l=Lcos θ=Lcos 60°=L。
7.[2015·杭州]如图26-7所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(2)木棒的重力作用点在其长度二分之一处,随
拉开角度θ的增加,拉力F将如何变化 并推导
拉力F与角度θ的关系式。
图26-7
解:(2)通过观察发现,随着角度θ的增大,l1减小,l2增大,根据杠杆平衡条件可得,F=,所以拉力F将逐渐增大。根据杠杆平衡条件得Fl1=Gl2,即F·lcos θ=G·lsin θ,则F=Gtan θ。
重点一
探究杠杆的平衡条件
例1 小金在探究杠杆的平衡条件时,改变杠杆两测悬挂钩码的个数,改变悬挂点到支点的距离,直至杠杆平衡,分别记录下此时动力F1、动力臂l1、阻力F2和阻力臂l2的数值,并将实验数据记录在表格中。
【数据记录】实验数据记录如下表所示
【实验结论】 ,公式表示:
。
实验序号 动力F1/牛 动力臂l1/厘米 阻力F2/牛 阻力臂l2/厘米
1 2 4 4 2
2 6 2 3 4
3 4 6 3 8
动力×动力臂=阻力×阻力臂
F1L1=F2L2
【交流与反思】
(1)实验前杠杆的调节:左高 调,右高 调。平衡后实验过程中 (选填“能”或“不能”)再调节平衡螺母。
左
右
不能
(2)图26-8甲中杠杆静止,此时杠杆平衡吗 ;实验过程中将杠杆调成水平平衡的目的是 。
图26-8
平衡
便于直接测量力臂
(3)有同学根据图乙所示的实验发现“2+3=3+2”,于是得出结论:“动力+动力臂=阻力+阻力臂”,这样做至少存在两个问题:① ;② 。
图26-8
不同的科学量不能相加减
实验次数太少,存在偶然性
(4)①另有同学通过图乙所示的实验得出结论:
动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离,请评价这个结论 (填序号)。
A.这个结论是完全错误的
B.这个结论是完全正确的
C.这个结论不具普遍意义
图26-8
C
②为了证明你的评价,可以怎样操作 应该在原实验基础上再做如图 所示的实验,该实验可以更好地认识力臂的概念。
③将钩码换成弹簧测力计的优点是
,缺点是
_________________________________
。
图26-8
丙
能直接测出拉力的大小
不能保证拉力方向一直竖直,拉力倾斜时不能直接读出力臂
④如图丙所示,弹簧测力计由竖直拉杠杆变成倾斜拉杠杆,弹簧测力计示数的变化是 ,原因是_______________。
图26-8
由小变大
力臂由大变小
(5)当用图丁所示装置进行实验时,发现得出的结论与“ ”不符合,原因是
。
图26-8
动力×动力臂=阻力×阻力臂
杠杆自身重力对实验有影响
(6)多次实验的目的是 。
(7)动力×动力臂的单位是“牛·米”,可以写成“焦”吗 为什么 _____________________________
________________________________
。
图26-8
避免实验的偶然性,使结论具有普遍性
不可以,因为动力臂的长度不是在力的方向上通过的距离,所以相乘的结果不是功
(8)实验中,用图戊所示的方式悬挂钩码,杠杆也能水平平衡(杠杆上每格等距),但老师却往往提醒大家不要采用这种方式,这主要是因为该种方式 (填序号)。
A.一个人无法独立操作
B.需要使用太多的钩码
C.力臂与杠杆不重合
D.力和力臂数目过多,不利于寻找
规律
图26-8
D
【变式1】[2019·宁波模拟]在“探究杠杆平衡条件”实验中,小科用一块T形板对实验装置进行改进。如图26-9甲所示,T形板上有槽口ab和卡口cd,T形板通
过槽口ab可以绕着杠杆的O点自由旋转
并上下移动,弹簧测力计与一根质量可以
忽略的碳素细棒MN相连,碳素细棒MN
刚好卡入T形板的卡口cd,如图乙所示。
图26-9
(1)小想认为要完成这个实验,还需要一把刻度尺,但小科认为只要在T形板上稍微进行改进,不添加器材也可完成实验。小科对T形板进行的改进方法是
。
(2)利用这个装置进行实验的优点为
__________________________________
。
图26-9
在T形板的槽口ab上标上刻度
可以改变拉力方向,且方便测量出相应的力臂长度
(3)小科在实验过程中,保持阻力、阻力臂不变,在杠杆水平平衡时,测出每一组动力臂l1和动力F1的数据,并利用实验数据绘制了F1与l1的关系图像,如图丙所示。请根
据图像推算,当l1为5 cm时,F1为 N。
图26-9
6
【变式2】[2018·湖州模拟]某兴趣小组利用厚纸板来探究杠杆的平衡条件,厚纸板上每间隔相同距离有个小孔。现用细绳将纸板悬挂起来,如图26-10甲所示。
图26-10
(1)实验中,小明在A点挂了1个钩码,如图乙所示,则需要在B点挂 个钩码才能使杠杆平衡。
图26-10
3
(2)小红认为:在力臂大小不变时,改变力的作用点到支点的距离,不会影响平衡。小红该怎样操作才能证明她的想法
。
图26-10
将其中一端钩码悬挂的位置上移(或下移动)1格(或2格)
(3)小军进行如图丙所示的实验,松手后发现杠杆不能保持水平平衡。请分析其原因是 。
图26-10
受厚纸板自身重力的影响
重点二
最小力问题
例2 [2020·湖州]为了防止门被风吹动,常在门背后和墙上安装如图26-11甲所示的“门吸”。如图乙所示是简化后的模型。门可以绕轴O自由转动,门宽为1.2 m。“门吸”与O位置关系、“门吸”引力
大小和方向如图乙所示。
(摩擦力忽略不计)
甲
乙
图26-11
(1)关门所需的最小力F是 N。
(2)在图乙中画出F的作用点和方向。
解:(2)如图所示
4
【名师点睛】
解决最小力问题的步骤:(1)找到杠杆上离支点最远的那个点;(2)连接支点和这个最远点,这条连线就是最大力臂;(3)作垂直于这条最大力臂的力就是最小力,要注意的是力的方向应能使杠杆平衡。
【变式3】[2014·丽水]如图26-12所示,杠杆OAB能绕O点转动,在A点挂一重物G,为保持杠杆在水平位置平衡,在B点分别作用的四个力中最小的是( )
A.F1 B.F2
C.F3 D.F4
图26-12
C
1.[2020·温州乐清模拟]各式各样的剪刀都是一对对的杠杆。要剪开较硬的物体,图26-13所示的剪刀中最合适的是 ( )
图26-13
A
B
C
D
B
2.[2019·衢州]如图26-14所示是起重机用四种方案将地面上的一棵大树扶起的瞬间,其中拉力最小的是( )
A
B
C
D
图26-14
C
3.如图26-15所示的四幅图中,力F的力臂画法错误的是 ( )
图26-15
D
4.[2017·嘉兴]如图26-16所示是一种切甘蔗用的铡刀的示意图。下列有关说法正确的是 ( )
A.刀刃很薄可以增大压力
B.铡刀实质上是一种费力杠杆
C.甘蔗放在a点比b点更易被切断
D.手沿F1方向用力比沿F2方向更省力
图26-16
C
5.[2018·衢州]如图26-17所示是汽车起重机,其中A、B组成滑轮组(结构如示意图所示),C杆伸缩可改变吊臂的长短,D杆伸缩可改变吊臂与水平面的角度,O为吊臂的转动轴。装在E里的电动机牵引钢丝绳,利用滑轮组提升重物,H为在车身外侧增加的支柱,F为吊臂顶端受到的竖直向下的力。
图26-17
下列有关汽车起重机的叙述中错误的是 ( )
A.滑轮组中A滑轮用于改变力的方向
B.当C杆伸长时吊臂对D杆的压力将变大
C.当D杆伸长时力F的力臂将变小
D.H的作用是工作时以防翻车和避免轮胎受到的压力过大
A
6.如图26-18所示,杠杆OA可绕支点O转动,B处挂一重物G,A处施加一竖直向上的力F。当杠杆和竖直墙之间夹角逐渐增大时,为使杠杆平衡,则 ( )
A.F大小不变,且FB.F大小不变,且F>G
C.F逐渐减小,且F>G
D.F逐渐增大,且F图26-18
A
7.如图26-19所示的轻质杠杆,AOA.杠杆仍保持平衡
B.杠杆的A端向下倾斜
C.杠杆的B端向下倾斜
D.无法判断
图26-19
A
8.[2021·绍兴]我国古代记录传统手工技术的著作《天工开物》里记载了一种捣谷用的舂,“横木穿插碓头,硬嘴为铁,足踏其末而舂之”,如图26-20甲所示。若碓头质量为20 kg,不计横木的重力和摩擦。
(1)如图乙所示为脚用力向下踩
舂时在某一位置的示意图,O点
为支点,F2为阻力,请在图中作出阻力臂l2,此时舂属于________ (选填“省力”“等臂”或“费力”)杠杆。
图26-20
l2
费力
(2)若每次碓头上升的高度为0.6 m,1 min内撞击臼中的谷粒20次,则碓头重力做功的功率为 W。(g取10 N/kg)
图26-20
40
9.[2020·温州瑞安一模]如图26-21所示,要想用一个最小的力,推着这个圆筒越过障碍物,试在图中画出此力的作用点和方向。
如图所示
图26-21
10.[2021·宁波节选]反思是一种良好的学习品质。
一根轻质硬棒AB,在力的作用下能绕固定点O转动。现在硬棒AB上施加两个力F1和F2,O点到F1和F2的作用线的距离分别为d1和d2。小宁认为,只要满足F1d1=F2d2,则硬棒AB一定保持静止或匀速转动状态。你认为小宁的想法正确吗 请说出你的理由。
解:小宁的想法不正确,F1与F2必须是一个为使杠杆绕支点转动的动力,另一个为阻碍杠杆转动的阻力,然后再满足F1l1= F2l2的条件杠杆才能平衡,即杠杆一定保持静止或匀速转动状态;若硬棒AB上施加的两个力F1和F2使杠杆绕支点转动的方向相同,那么即使满足F1d1=F2d2,则硬棒AB也不能保持静止或匀速转动状态。
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(1)此木料的密度为多少
(2)如图W16-22所示,甲、乙两人分别在
A点和B点共同扛起此木料并恰好水平,其中AO=BO,O为木料的中点。求此时乙对木料的作用力大小。
(3)若在(2)中当乙对木料施加的力的作用点从B点向O点靠近时,请列式分析此过程中甲对木料作用力大小的变化情况。
图26-22
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(1)此木料的密度为多少
图26-22
解:(1)木料的密度ρ=
=600 kg/m3。
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(2)如图26-22所示,甲、乙两人分别在A点和B点共同扛起此木料并恰好水平,其中AO=BO,O为木料的中点。求此时乙对木料的作用力大小。
图26-22
解:(2)木料的重力
G=mg=60 kg×10 N/kg=600 N,
以A为支点,根据杠杆平衡条件F1l1=F2l2得,
F乙×AB=G×AO,则F乙==600 N×=300 N。
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(3)若在(2)中当乙对木料施加的力的作用点从B点向O点靠近时,请列式分析此过程中甲对木料作用力大小的变化情况。
图26-22
解:(3)当乙对木料施加的力的作用点向O点
靠近时,此时作用点记为B',
以A为支点,根据杠杆平衡条件
F1l1=F2l2得,
F乙×AB'=G×AO,则F乙=,
因为AB'减小,而G×AO不变,所以F乙变大,
而F乙+F甲=G,所以,甲对木料的作用力F甲变小。
第26课时 简单机械——杠杆
●知识体系梳理
●重难考点精讲
●当堂限时训练
知识体系
固定点
动力作用线
阻力作用线
动力×动力臂=阻力×阻力臂
>
<
扳手
开瓶器
=
=
天平
定滑轮
<
>
钓鱼竿
重点梳理
区别力臂和支点到力的作用点的距离
力臂是 到 的距离,是点到线的距离;支点到力的作用点的距离是点到点的距离。
这两者,当 的方向和 垂直时,两者相等;当两者不垂直时,两者不等。
支点
力的作用线
力
杠杆
对点练习
1.[2021·金华]生活中处处有科学。如图26-1所示的日常工具在使用时属于费力杠杆的是( )
图26-1
C
2.[2021·温州]停放自行车时,若要从如图26-2所示的四点中选择一点施加竖直向上的力,将后轮略微提起。其中最省力的点是 ( )
A.A点 B.B点
C.C点 D.D点
图26-2
D
3.[2017·杭州]小金将长为0.6 m、质量可忽略不计的木棒搁在肩上,棒的后端A点挂一个重40 N的物体,肩上支点O离后端A点的距离为0.2 m,他用手压住前端B点使木棒保持水平平衡,如图26-3所示。小金的质量为50 kg,则此时手压
木棒的力大小为 N,肩对木棒的支持力大小
为 N,人对地面的压力大小为 N。
(g取10 N/kg)
图26-3
20
60
540
4.[2018·杭州]如图26-4所示,将长为1.2米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为 30牛的物体,在B端挂一个重为G的物体。
(1)若G=30 牛,则台面受到木棒的压力为 牛。
(2)若要使木棒右端下沉,B端挂的物体至少为
牛。
(3)若B端挂物体后,木棒仍在水平台面上静止,则G
的取值范围为 牛。
图26-4
60
90
10~90
5.[2020·衢州]在实际生活中,常用螺丝刀将螺丝钉拧进(出)物体。图26-5甲中正在拧螺丝钉的螺丝刀,可视为如图乙所示的杠杆AOB,其中O为支点,B为阻力作用点,F2为阻力,动力作用在手柄上。
(1)图甲中的螺丝刀属于 杠杆。
(2)在图乙中画出F2对应的最小动力F1的
示意图。
图26-5
省力
解:(2)如图所示
6.[2016·杭州]小金用如图26-6所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦不计)
图26-6
(1)重为5 N的钩码挂在A点时,人的拉力F始终为4 N。钩码上升0.3 m时,动力作用点C上升0.5 m,此时机械效率η1为多大
(2)小金为了进一步探究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5 m。问:与第一次相比,人的拉力F将________ (选填“变大”“变小”或“不变”)。比较此时的机械效率η2与η1的大小,并用学过的知识给以推导。
(1)重为5 N的钩码挂在A点时,人的拉力F始终为4 N。钩码上升0.3 m时,动力作用点C上升0.5 m,此时机械效率η1为多大
图26-6
解:(1)η1=×100%=×100%
=×100%=75%。
(2)小金为了进一步探究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5 m。问:与第一次相比,人的拉力F将________ (选填“变大”“变小”或“不变”)。比较此时的机械效率η2与η1的大小,并用学过的知识给以推导。
图26-6
变小
推导过程:第二次提升时,杠杆动力作用点升高的高度不变,因此克服杠杆自重所做的额外功不变。而被提升的钩码由于靠近支点,因此钩码升高的高度减小,有用功减小。机械效率
η=×100%=×100%=×100%,
而W有用2
(1)画出θ=60°时拉力F的力臂l,并计算力臂的
大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化 并推导拉力F与角度θ的关系式。
图26-7
7.[2015·杭州]如图26-7所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)画出θ=60°时拉力F的力臂l,并计算力臂的
大小。
图26-7
解:(1)如图所示
l=Lcos θ=Lcos 60°=L。
7.[2015·杭州]如图26-7所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(2)木棒的重力作用点在其长度二分之一处,随
拉开角度θ的增加,拉力F将如何变化 并推导
拉力F与角度θ的关系式。
图26-7
解:(2)通过观察发现,随着角度θ的增大,l1减小,l2增大,根据杠杆平衡条件可得,F=,所以拉力F将逐渐增大。根据杠杆平衡条件得Fl1=Gl2,即F·lcos θ=G·lsin θ,则F=Gtan θ。
重点一
探究杠杆的平衡条件
例1 小金在探究杠杆的平衡条件时,改变杠杆两测悬挂钩码的个数,改变悬挂点到支点的距离,直至杠杆平衡,分别记录下此时动力F1、动力臂l1、阻力F2和阻力臂l2的数值,并将实验数据记录在表格中。
【数据记录】实验数据记录如下表所示
【实验结论】 ,公式表示:
。
实验序号 动力F1/牛 动力臂l1/厘米 阻力F2/牛 阻力臂l2/厘米
1 2 4 4 2
2 6 2 3 4
3 4 6 3 8
动力×动力臂=阻力×阻力臂
F1L1=F2L2
【交流与反思】
(1)实验前杠杆的调节:左高 调,右高 调。平衡后实验过程中 (选填“能”或“不能”)再调节平衡螺母。
左
右
不能
(2)图26-8甲中杠杆静止,此时杠杆平衡吗 ;实验过程中将杠杆调成水平平衡的目的是 。
图26-8
平衡
便于直接测量力臂
(3)有同学根据图乙所示的实验发现“2+3=3+2”,于是得出结论:“动力+动力臂=阻力+阻力臂”,这样做至少存在两个问题:① ;② 。
图26-8
不同的科学量不能相加减
实验次数太少,存在偶然性
(4)①另有同学通过图乙所示的实验得出结论:
动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离,请评价这个结论 (填序号)。
A.这个结论是完全错误的
B.这个结论是完全正确的
C.这个结论不具普遍意义
图26-8
C
②为了证明你的评价,可以怎样操作 应该在原实验基础上再做如图 所示的实验,该实验可以更好地认识力臂的概念。
③将钩码换成弹簧测力计的优点是
,缺点是
_________________________________
。
图26-8
丙
能直接测出拉力的大小
不能保证拉力方向一直竖直,拉力倾斜时不能直接读出力臂
④如图丙所示,弹簧测力计由竖直拉杠杆变成倾斜拉杠杆,弹簧测力计示数的变化是 ,原因是_______________。
图26-8
由小变大
力臂由大变小
(5)当用图丁所示装置进行实验时,发现得出的结论与“ ”不符合,原因是
。
图26-8
动力×动力臂=阻力×阻力臂
杠杆自身重力对实验有影响
(6)多次实验的目的是 。
(7)动力×动力臂的单位是“牛·米”,可以写成“焦”吗 为什么 _____________________________
________________________________
。
图26-8
避免实验的偶然性,使结论具有普遍性
不可以,因为动力臂的长度不是在力的方向上通过的距离,所以相乘的结果不是功
(8)实验中,用图戊所示的方式悬挂钩码,杠杆也能水平平衡(杠杆上每格等距),但老师却往往提醒大家不要采用这种方式,这主要是因为该种方式 (填序号)。
A.一个人无法独立操作
B.需要使用太多的钩码
C.力臂与杠杆不重合
D.力和力臂数目过多,不利于寻找
规律
图26-8
D
【变式1】[2019·宁波模拟]在“探究杠杆平衡条件”实验中,小科用一块T形板对实验装置进行改进。如图26-9甲所示,T形板上有槽口ab和卡口cd,T形板通
过槽口ab可以绕着杠杆的O点自由旋转
并上下移动,弹簧测力计与一根质量可以
忽略的碳素细棒MN相连,碳素细棒MN
刚好卡入T形板的卡口cd,如图乙所示。
图26-9
(1)小想认为要完成这个实验,还需要一把刻度尺,但小科认为只要在T形板上稍微进行改进,不添加器材也可完成实验。小科对T形板进行的改进方法是
。
(2)利用这个装置进行实验的优点为
__________________________________
。
图26-9
在T形板的槽口ab上标上刻度
可以改变拉力方向,且方便测量出相应的力臂长度
(3)小科在实验过程中,保持阻力、阻力臂不变,在杠杆水平平衡时,测出每一组动力臂l1和动力F1的数据,并利用实验数据绘制了F1与l1的关系图像,如图丙所示。请根
据图像推算,当l1为5 cm时,F1为 N。
图26-9
6
【变式2】[2018·湖州模拟]某兴趣小组利用厚纸板来探究杠杆的平衡条件,厚纸板上每间隔相同距离有个小孔。现用细绳将纸板悬挂起来,如图26-10甲所示。
图26-10
(1)实验中,小明在A点挂了1个钩码,如图乙所示,则需要在B点挂 个钩码才能使杠杆平衡。
图26-10
3
(2)小红认为:在力臂大小不变时,改变力的作用点到支点的距离,不会影响平衡。小红该怎样操作才能证明她的想法
。
图26-10
将其中一端钩码悬挂的位置上移(或下移动)1格(或2格)
(3)小军进行如图丙所示的实验,松手后发现杠杆不能保持水平平衡。请分析其原因是 。
图26-10
受厚纸板自身重力的影响
重点二
最小力问题
例2 [2020·湖州]为了防止门被风吹动,常在门背后和墙上安装如图26-11甲所示的“门吸”。如图乙所示是简化后的模型。门可以绕轴O自由转动,门宽为1.2 m。“门吸”与O位置关系、“门吸”引力
大小和方向如图乙所示。
(摩擦力忽略不计)
甲
乙
图26-11
(1)关门所需的最小力F是 N。
(2)在图乙中画出F的作用点和方向。
解:(2)如图所示
4
【名师点睛】
解决最小力问题的步骤:(1)找到杠杆上离支点最远的那个点;(2)连接支点和这个最远点,这条连线就是最大力臂;(3)作垂直于这条最大力臂的力就是最小力,要注意的是力的方向应能使杠杆平衡。
【变式3】[2014·丽水]如图26-12所示,杠杆OAB能绕O点转动,在A点挂一重物G,为保持杠杆在水平位置平衡,在B点分别作用的四个力中最小的是( )
A.F1 B.F2
C.F3 D.F4
图26-12
C
1.[2020·温州乐清模拟]各式各样的剪刀都是一对对的杠杆。要剪开较硬的物体,图26-13所示的剪刀中最合适的是 ( )
图26-13
A
B
C
D
B
2.[2019·衢州]如图26-14所示是起重机用四种方案将地面上的一棵大树扶起的瞬间,其中拉力最小的是( )
A
B
C
D
图26-14
C
3.如图26-15所示的四幅图中,力F的力臂画法错误的是 ( )
图26-15
D
4.[2017·嘉兴]如图26-16所示是一种切甘蔗用的铡刀的示意图。下列有关说法正确的是 ( )
A.刀刃很薄可以增大压力
B.铡刀实质上是一种费力杠杆
C.甘蔗放在a点比b点更易被切断
D.手沿F1方向用力比沿F2方向更省力
图26-16
C
5.[2018·衢州]如图26-17所示是汽车起重机,其中A、B组成滑轮组(结构如示意图所示),C杆伸缩可改变吊臂的长短,D杆伸缩可改变吊臂与水平面的角度,O为吊臂的转动轴。装在E里的电动机牵引钢丝绳,利用滑轮组提升重物,H为在车身外侧增加的支柱,F为吊臂顶端受到的竖直向下的力。
图26-17
下列有关汽车起重机的叙述中错误的是 ( )
A.滑轮组中A滑轮用于改变力的方向
B.当C杆伸长时吊臂对D杆的压力将变大
C.当D杆伸长时力F的力臂将变小
D.H的作用是工作时以防翻车和避免轮胎受到的压力过大
A
6.如图26-18所示,杠杆OA可绕支点O转动,B处挂一重物G,A处施加一竖直向上的力F。当杠杆和竖直墙之间夹角逐渐增大时,为使杠杆平衡,则 ( )
A.F大小不变,且F
C.F逐渐减小,且F>G
D.F逐渐增大,且F
A
7.如图26-19所示的轻质杠杆,AO
B.杠杆的A端向下倾斜
C.杠杆的B端向下倾斜
D.无法判断
图26-19
A
8.[2021·绍兴]我国古代记录传统手工技术的著作《天工开物》里记载了一种捣谷用的舂,“横木穿插碓头,硬嘴为铁,足踏其末而舂之”,如图26-20甲所示。若碓头质量为20 kg,不计横木的重力和摩擦。
(1)如图乙所示为脚用力向下踩
舂时在某一位置的示意图,O点
为支点,F2为阻力,请在图中作出阻力臂l2,此时舂属于________ (选填“省力”“等臂”或“费力”)杠杆。
图26-20
l2
费力
(2)若每次碓头上升的高度为0.6 m,1 min内撞击臼中的谷粒20次,则碓头重力做功的功率为 W。(g取10 N/kg)
图26-20
40
9.[2020·温州瑞安一模]如图26-21所示,要想用一个最小的力,推着这个圆筒越过障碍物,试在图中画出此力的作用点和方向。
如图所示
图26-21
10.[2021·宁波节选]反思是一种良好的学习品质。
一根轻质硬棒AB,在力的作用下能绕固定点O转动。现在硬棒AB上施加两个力F1和F2,O点到F1和F2的作用线的距离分别为d1和d2。小宁认为,只要满足F1d1=F2d2,则硬棒AB一定保持静止或匀速转动状态。你认为小宁的想法正确吗 请说出你的理由。
解:小宁的想法不正确,F1与F2必须是一个为使杠杆绕支点转动的动力,另一个为阻碍杠杆转动的阻力,然后再满足F1l1= F2l2的条件杠杆才能平衡,即杠杆一定保持静止或匀速转动状态;若硬棒AB上施加的两个力F1和F2使杠杆绕支点转动的方向相同,那么即使满足F1d1=F2d2,则硬棒AB也不能保持静止或匀速转动状态。
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(1)此木料的密度为多少
(2)如图W16-22所示,甲、乙两人分别在
A点和B点共同扛起此木料并恰好水平,其中AO=BO,O为木料的中点。求此时乙对木料的作用力大小。
(3)若在(2)中当乙对木料施加的力的作用点从B点向O点靠近时,请列式分析此过程中甲对木料作用力大小的变化情况。
图26-22
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(1)此木料的密度为多少
图26-22
解:(1)木料的密度ρ=
=600 kg/m3。
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(2)如图26-22所示,甲、乙两人分别在A点和B点共同扛起此木料并恰好水平,其中AO=BO,O为木料的中点。求此时乙对木料的作用力大小。
图26-22
解:(2)木料的重力
G=mg=60 kg×10 N/kg=600 N,
以A为支点,根据杠杆平衡条件F1l1=F2l2得,
F乙×AB=G×AO,则F乙==600 N×=300 N。
11.[2021·杭州]已知一根质量分布均匀的圆柱体木料的质量为60 kg、体积为0.1 m3。(g取10 N/kg)
(3)若在(2)中当乙对木料施加的力的作用点从B点向O点靠近时,请列式分析此过程中甲对木料作用力大小的变化情况。
图26-22
解:(3)当乙对木料施加的力的作用点向O点
靠近时,此时作用点记为B',
以A为支点,根据杠杆平衡条件
F1l1=F2l2得,
F乙×AB'=G×AO,则F乙=,
因为AB'减小,而G×AO不变,所以F乙变大,
而F乙+F甲=G,所以,甲对木料的作用力F甲变小。
同课章节目录
