人教版数学七年级下册 第六章实数复习课件(共40张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第六章实数复习课件(共40张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 954.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 10:55:00 | ||
图片预览





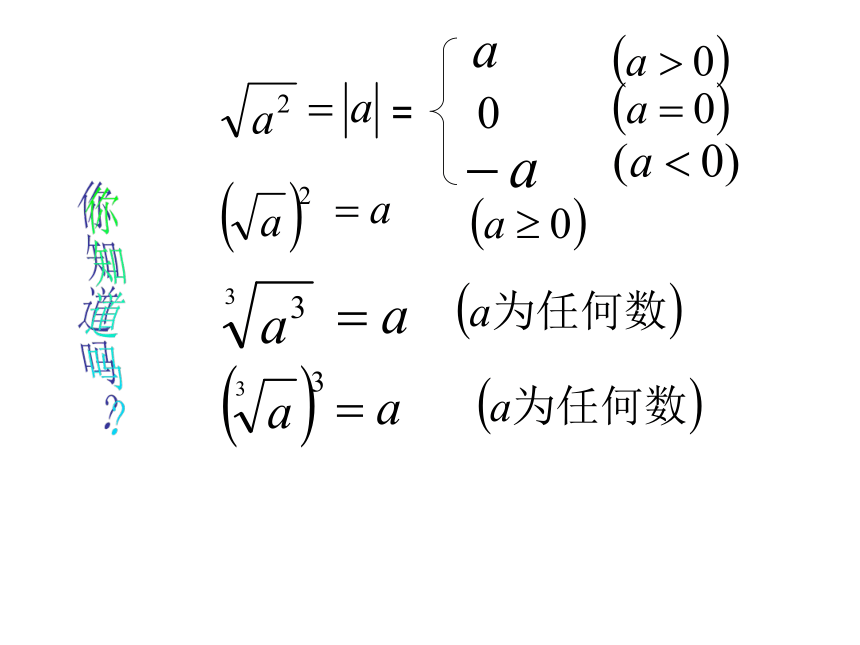



文档简介
(共40张PPT)
七年级
第六章实数的复习
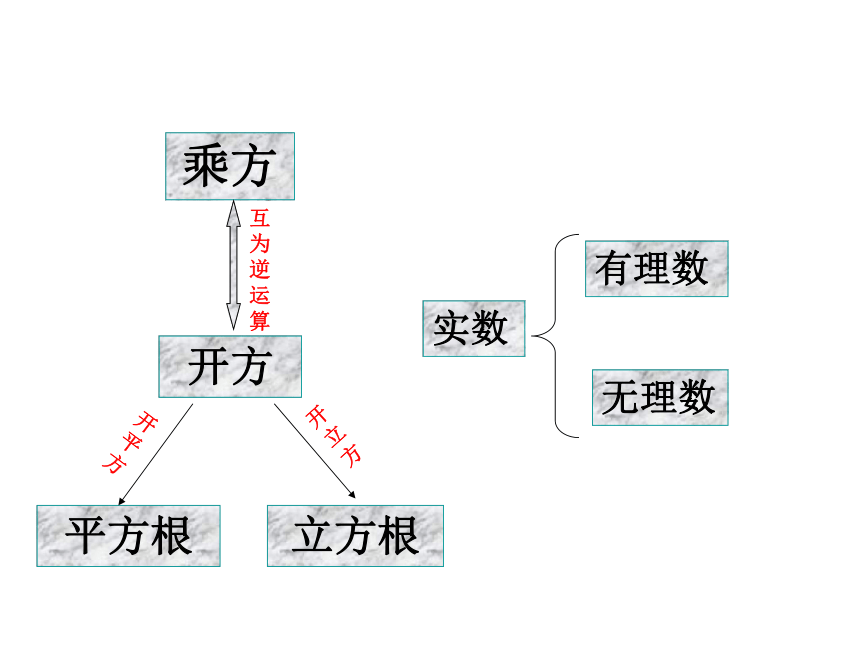
乘方
开方
平方根
立方根
实数
有理数
无理数
互为逆运算
开平方
开立方
定义
一般地,如果一个正数 x 的平方等于 a(x2 = a),那么这个正数 x 就叫做 a 的
算术平方根
a 的算术平方根记作
读作
“ 根号a ”
根号
被开方数
规定:0的算术平方根等于0
如102 = 100
则100的算术平方根
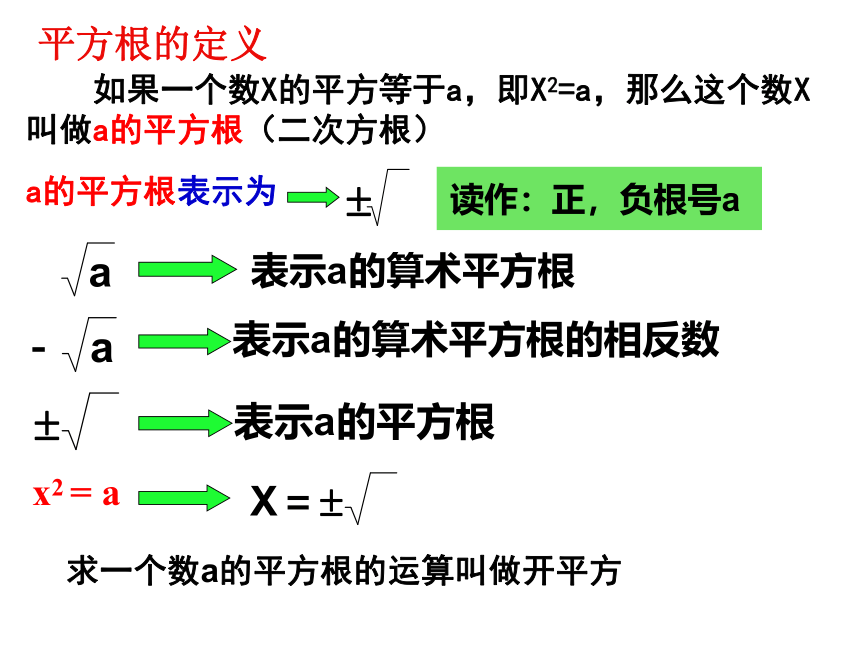
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
a的平方根表示为
x2 = a
求一个数a的平方根的运算叫做开平方
平方根的定义
平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
正数有立方根吗?如果有,有几个
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
(1)立方根的特征
(2)平方根和立方根的异同点
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
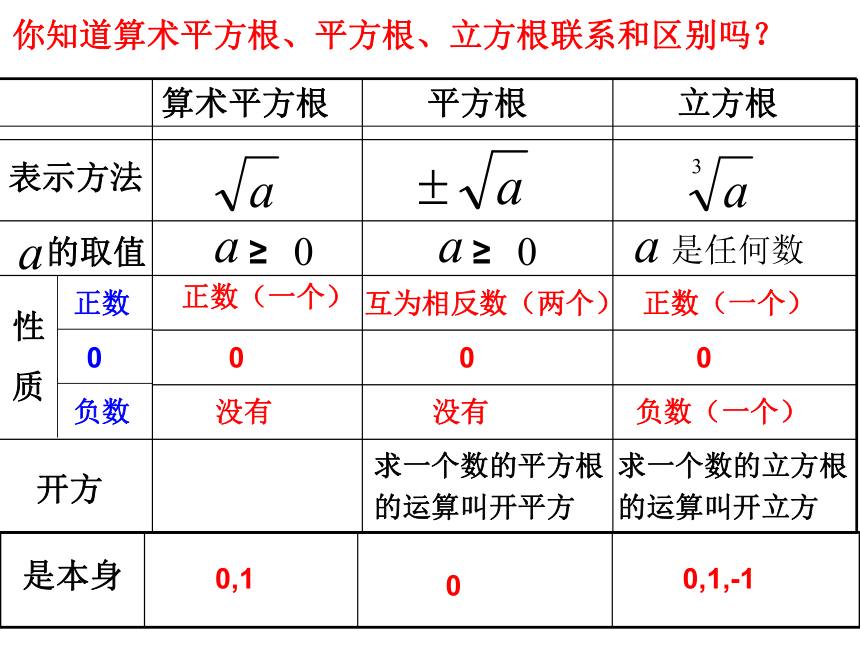
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
=
2.说出下列各数的立方根:
1.说出下列各数的平方根和算术平方根:
(1)169
(2)0.16
(4)100
(3)
(5)
(5)
相反数:
绝对值:
倒数:
平方根:
实数的相关概念
类型二 实数的相反数、倒数和绝对值的意义
例2 求下列各数相反数、倒数和绝对值。
⑴ ⑵ ⑶ ⑷
类型二 实数的相反数、倒数和绝对值的意义
例2 求下列各数相反数、倒数和绝对值。
⑴ ⑵ ⑶ ⑷
类型三 实数的大小比较
例3 比较 与 的大小
例4 比较 与 的大小
例5 比较 与 的大小
例6比较 的大小
例7 比较 的大小
实数与数轴
数轴三要素:
原点、正方向、单位长度
0
1
2
3
4
5
-1
-2
-3
-4
实数与数轴上的点一一对应
类型四 数轴上的点与实数一一对应的关系
例8、如图所示:数轴上表示1, 的对应点分别为A, B, 点B关于点A的对称点为点C,点C关于点A的对称点为点B(即AC=AB),则点C所表示的数是( )
0
1
2
C
A
B
A、 B、 C、 D、
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
有限小数及无限循环小数
无限不循环小数
一般有三种情况
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
类型五 实数的运算
例9 计算
⑴求5的算术平方根与2的算术平方根之和(精确到0.01)
⑵
⑶
一、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
不要搞错了
64
±8
8
-4
______.
-4,-3,-2,-1,
0,1,2,3
下列说法正确的是( )
B
1.说出下列各数的平方根
(1) (2) (3)
(x≥-4)
(X为任意实数)
(X为任意实数)
当方程中出现平方时,若有解,一般都有两个解
当方程中出现立方时,一般都有一个解
1.
解:
2.
解:
1.
掌握规律
2.若- = ,则m的值是 ( )
A B C D
3. 若 成立,则x的取值范围是( )
A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数
B
B
A
D
4.若 =4-x成立,则x的取值范围是( )
A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
一.求下列各式的值:
1. 2.
3. (x≥1) 4. (x≤1)
二.已知实数a、b、c,在数轴上的位置如下图所示,
试化简:
(1) - |a-b|+|c-a|+
(2)|a+b-c|+|b-2c|+
-2
是负数
等于它的相反数
是正数
等于本身
是负数
里面的数的符号
化简绝对值要看它
典型例题解析
例1、(1) 的倒数是 ;
(2) -2的绝对值是 ;
。
例3、比较大小: 与
例4、已知实数a、b在数轴上对应点的位置如图1-2;
化简:
解:∵(-2+ )-(-2+ )=-2+ +2- = - >0
∴-2+ >-2+
另解:直接由正负决定-2+ >-2+
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+ =(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
b a o
x
例5、若
求 的值。
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-43,b=34
∴a2003b2004=(-4/3)2003·(3/4)2004=-34
自测:
1.如果一个数的平方根为a+1和2a-7, 求这
个数?
3.已知y= 求2(x+y)的平方根
4.已知5+ 的小数部分为 m, 7- 的小数部分为n,求m+n的值
5.已知满足 ,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
0
25
6、a、b互为相反数,c与d互为倒数,则a+1+b+
cd= 。
2
11、实数a,b,c,d在数轴上的对应点如图1-1所示,则
它们从小到大的顺序是 。
c d 0 b a
图1-1-1
其中:
ca+b
-d-c
b-c
a-d
12、π的整数部分为3,则它
的小数部分是 ;
π-3
10、比较大小:
二、选择题:
1、(-3)2的算术平方根是( )
(A)无意义
(B)±3
(C)-3
(D) 3
二、选择题:
1、(-3)2的算术平方根是( )
(A)无意义
(B)±3
(C)-3
(D) 3
3、下列语句中正确的是( )
(A)
-9的平方根是-3
(B)
9的平方根是3
(C)
9的算术平方根是
(D) 9的算术平方根是3
D
4、下列运算中,正确的是( )
A
5、
的平方根是( )
(A)
(C) 5
(B)
(D)
6、下列运算正确的是( )
D
D
1.如果一个数的平方根为a+1和2a-7, 求这个数
3.已知y= 求2(x+y)的平方根
4.已知5+ 的小数部分为 m, 7- 的小数部分为n,求m+n的值
5.已知满足 ,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
练习
七年级
第六章实数的复习
乘方
开方
平方根
立方根
实数
有理数
无理数
互为逆运算
开平方
开立方
定义
一般地,如果一个正数 x 的平方等于 a(x2 = a),那么这个正数 x 就叫做 a 的
算术平方根
a 的算术平方根记作
读作
“ 根号a ”
根号
被开方数
规定:0的算术平方根等于0
如102 = 100
则100的算术平方根
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
a的平方根表示为
x2 = a
求一个数a的平方根的运算叫做开平方
平方根的定义
平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
正数有立方根吗?如果有,有几个
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
(1)立方根的特征
(2)平方根和立方根的异同点
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
=
2.说出下列各数的立方根:
1.说出下列各数的平方根和算术平方根:
(1)169
(2)0.16
(4)100
(3)
(5)
(5)
相反数:
绝对值:
倒数:
平方根:
实数的相关概念
类型二 实数的相反数、倒数和绝对值的意义
例2 求下列各数相反数、倒数和绝对值。
⑴ ⑵ ⑶ ⑷
类型二 实数的相反数、倒数和绝对值的意义
例2 求下列各数相反数、倒数和绝对值。
⑴ ⑵ ⑶ ⑷
类型三 实数的大小比较
例3 比较 与 的大小
例4 比较 与 的大小
例5 比较 与 的大小
例6比较 的大小
例7 比较 的大小
实数与数轴
数轴三要素:
原点、正方向、单位长度
0
1
2
3
4
5
-1
-2
-3
-4
实数与数轴上的点一一对应
类型四 数轴上的点与实数一一对应的关系
例8、如图所示:数轴上表示1, 的对应点分别为A, B, 点B关于点A的对称点为点C,点C关于点A的对称点为点B(即AC=AB),则点C所表示的数是( )
0
1
2
C
A
B
A、 B、 C、 D、
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
有限小数及无限循环小数
无限不循环小数
一般有三种情况
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
类型五 实数的运算
例9 计算
⑴求5的算术平方根与2的算术平方根之和(精确到0.01)
⑵
⑶
一、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
不要搞错了
64
±8
8
-4
______.
-4,-3,-2,-1,
0,1,2,3
下列说法正确的是( )
B
1.说出下列各数的平方根
(1) (2) (3)
(x≥-4)
(X为任意实数)
(X为任意实数)
当方程中出现平方时,若有解,一般都有两个解
当方程中出现立方时,一般都有一个解
1.
解:
2.
解:
1.
掌握规律
2.若- = ,则m的值是 ( )
A B C D
3. 若 成立,则x的取值范围是( )
A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数
B
B
A
D
4.若 =4-x成立,则x的取值范围是( )
A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
一.求下列各式的值:
1. 2.
3. (x≥1) 4. (x≤1)
二.已知实数a、b、c,在数轴上的位置如下图所示,
试化简:
(1) - |a-b|+|c-a|+
(2)|a+b-c|+|b-2c|+
-2
是负数
等于它的相反数
是正数
等于本身
是负数
里面的数的符号
化简绝对值要看它
典型例题解析
例1、(1) 的倒数是 ;
(2) -2的绝对值是 ;
。
例3、比较大小: 与
例4、已知实数a、b在数轴上对应点的位置如图1-2;
化简:
解:∵(-2+ )-(-2+ )=-2+ +2- = - >0
∴-2+ >-2+
另解:直接由正负决定-2+ >-2+
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+ =(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
b a o
x
例5、若
求 的值。
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-43,b=34
∴a2003b2004=(-4/3)2003·(3/4)2004=-34
自测:
1.如果一个数的平方根为a+1和2a-7, 求这
个数?
3.已知y= 求2(x+y)的平方根
4.已知5+ 的小数部分为 m, 7- 的小数部分为n,求m+n的值
5.已知满足 ,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
0
25
6、a、b互为相反数,c与d互为倒数,则a+1+b+
cd= 。
2
11、实数a,b,c,d在数轴上的对应点如图1-1所示,则
它们从小到大的顺序是 。
c d 0 b a
图1-1-1
其中:
c
-d-c
b-c
a-d
12、π的整数部分为3,则它
的小数部分是 ;
π-3
10、比较大小:
二、选择题:
1、(-3)2的算术平方根是( )
(A)无意义
(B)±3
(C)-3
(D) 3
二、选择题:
1、(-3)2的算术平方根是( )
(A)无意义
(B)±3
(C)-3
(D) 3
3、下列语句中正确的是( )
(A)
-9的平方根是-3
(B)
9的平方根是3
(C)
9的算术平方根是
(D) 9的算术平方根是3
D
4、下列运算中,正确的是( )
A
5、
的平方根是( )
(A)
(C) 5
(B)
(D)
6、下列运算正确的是( )
D
D
1.如果一个数的平方根为a+1和2a-7, 求这个数
3.已知y= 求2(x+y)的平方根
4.已知5+ 的小数部分为 m, 7- 的小数部分为n,求m+n的值
5.已知满足 ,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
练习
