八上人教版 12.2 三角形全等的判定 第3课时(word版含答案)
文档属性
| 名称 | 八上人教版 12.2 三角形全等的判定 第3课时(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 16:26:26 | ||
图片预览

文档简介
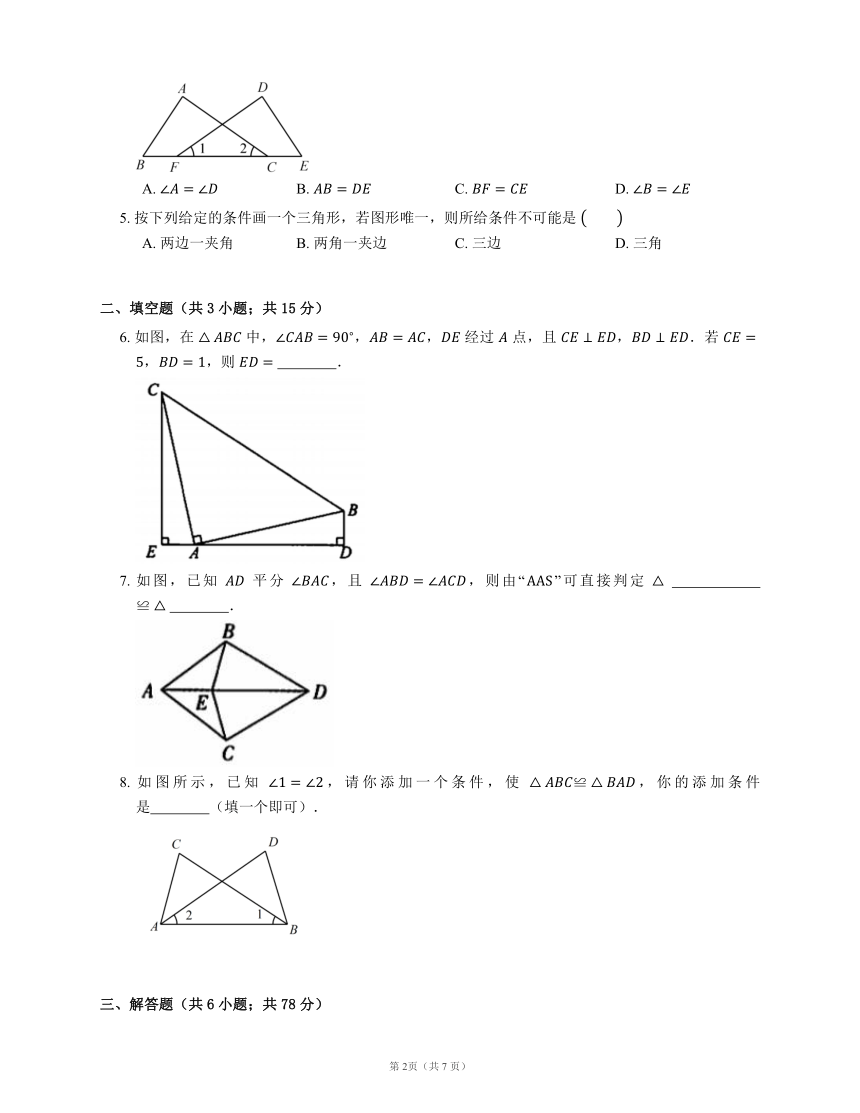
八上-第十二章 全等三角形-12.2 三角形全等的判定-第3课时 三角形全等的判定(三)
一、选择题(共5小题;共25分)
1. 如图,某同学把一块三角形的玻璃打破成了三块,现在要到玻璃店买一块同样大小的三角形玻璃,为了方便,他需要带的玻璃是
A. ① B. ② C. ③ D. 都不行
2. 如图,要测量河两岸相对的两点 , 的距离,先在 的垂线 上取两点 ,,使 ,再作出 的垂线 ,使点 ,, 在同一条直线上,可以证明 ,得到 ,因此测得 的长就是 的长,判定 最恰当的理由是
A. B. C. D.
3. 如图,点 在 上,点 在 上,且 ,那么补充下列一个条件后,仍无法判定 的是
A. B.
C. D.
4. 如图,,,如果根据“”判定 ,那么需要补充的条件是
A. B. C. D.
5. 按下列给定的条件画一个三角形,若图形唯一,则所给条件不可能是
A. 两边一夹角 B. 两角一夹边 C. 三边 D. 三角
二、填空题(共3小题;共15分)
6. 如图,在 中,,, 经过 点,且 ,.若 ,,则 .
7. 如图,已知 平分 ,且 ,则由“”可直接判定 .
8. 如图所示,已知 ,请你添加一个条件,使 ,你的添加条件是 (填一个即可).
三、解答题(共6小题;共78分)
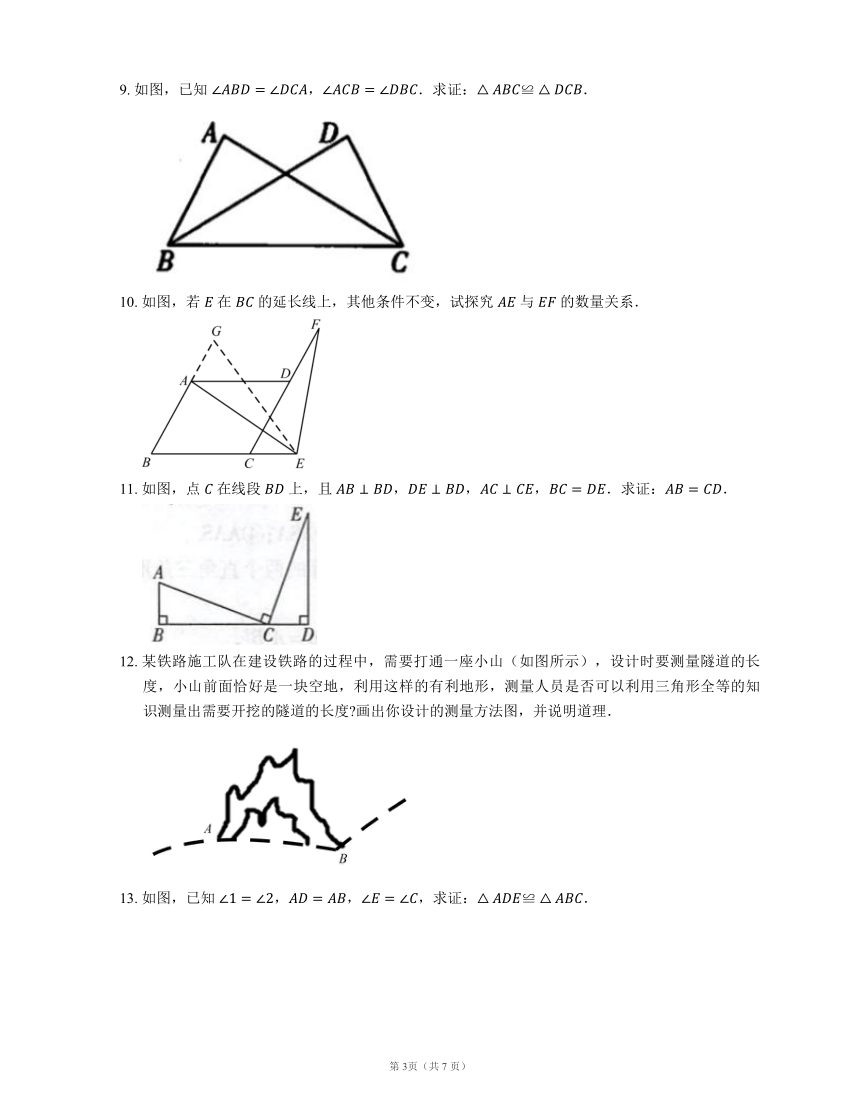
9. 如图,已知 ,.求证:.
10. 如图,若 在 的延长线上,其他条件不变,试探究 与 的数量关系.
11. 如图,点 在线段 上,且 ,,,.求证:.
12. 某铁路施工队在建设铁路的过程中,需要打通一座小山(如图所示),设计时要测量隧道的长度,小山前面恰好是一块空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道的长度 画出你设计的测量方法图,并说明道理.
13. 如图,已知 ,,,求证:.
14. 如图,过点 的射线 ,在射线 上截取线段 ,过点 的直线 不与射线 及直线 重合,过点 作 于点 ,过点 作 于点 .
(1)依题意补全图形;
(2)求证:.
答案
第一部分
1. A 【解析】根据题图可知,第①块不仅保留了原三角形的两个角还保留了两个角的夹边,则可以根据 来配一块完全一样的玻璃.
2. D 【解析】在 和 中,
.
3. B
4. A 【解析】需要补充的条件是 ,
在 和 中,
.
5. D
第二部分
6.
【解析】,,
,
,,,
,.
在 和 中,
,
,.
,,,
.
7. ,
【解析】因为 平分 ,
所以 .
又因为 ,,
所以由“”可直接判定 .
8. 或 或
第三部分
9. ,,
,即 .
在 和 中,
.
10. ,
在 的延长线上截取 ,
证 .
11. ,,,
.
,.
.
在 和 中,
.
.
12. 如图所示,在山前空地选取一个可以直接到达隧道两端 , 的一点 ,连接 并延长到点 ,使 ;连接 并延长到点 ,使 ,连接 ,并测出 的长度,则 的长度就是 , 间的距离.
理由如下:
在 和 中,
,,,
.
.
13. ,
,即 ,
在 和 中,
.
14. (1) 画法不唯一,如图所示.
(2) ,
,
,
,
,
,
,
,,
,
在 和 中,
.
第1页(共1 页)
一、选择题(共5小题;共25分)
1. 如图,某同学把一块三角形的玻璃打破成了三块,现在要到玻璃店买一块同样大小的三角形玻璃,为了方便,他需要带的玻璃是
A. ① B. ② C. ③ D. 都不行
2. 如图,要测量河两岸相对的两点 , 的距离,先在 的垂线 上取两点 ,,使 ,再作出 的垂线 ,使点 ,, 在同一条直线上,可以证明 ,得到 ,因此测得 的长就是 的长,判定 最恰当的理由是
A. B. C. D.
3. 如图,点 在 上,点 在 上,且 ,那么补充下列一个条件后,仍无法判定 的是
A. B.
C. D.
4. 如图,,,如果根据“”判定 ,那么需要补充的条件是
A. B. C. D.
5. 按下列给定的条件画一个三角形,若图形唯一,则所给条件不可能是
A. 两边一夹角 B. 两角一夹边 C. 三边 D. 三角
二、填空题(共3小题;共15分)
6. 如图,在 中,,, 经过 点,且 ,.若 ,,则 .
7. 如图,已知 平分 ,且 ,则由“”可直接判定 .
8. 如图所示,已知 ,请你添加一个条件,使 ,你的添加条件是 (填一个即可).
三、解答题(共6小题;共78分)
9. 如图,已知 ,.求证:.
10. 如图,若 在 的延长线上,其他条件不变,试探究 与 的数量关系.
11. 如图,点 在线段 上,且 ,,,.求证:.
12. 某铁路施工队在建设铁路的过程中,需要打通一座小山(如图所示),设计时要测量隧道的长度,小山前面恰好是一块空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道的长度 画出你设计的测量方法图,并说明道理.
13. 如图,已知 ,,,求证:.
14. 如图,过点 的射线 ,在射线 上截取线段 ,过点 的直线 不与射线 及直线 重合,过点 作 于点 ,过点 作 于点 .
(1)依题意补全图形;
(2)求证:.
答案
第一部分
1. A 【解析】根据题图可知,第①块不仅保留了原三角形的两个角还保留了两个角的夹边,则可以根据 来配一块完全一样的玻璃.
2. D 【解析】在 和 中,
.
3. B
4. A 【解析】需要补充的条件是 ,
在 和 中,
.
5. D
第二部分
6.
【解析】,,
,
,,,
,.
在 和 中,
,
,.
,,,
.
7. ,
【解析】因为 平分 ,
所以 .
又因为 ,,
所以由“”可直接判定 .
8. 或 或
第三部分
9. ,,
,即 .
在 和 中,
.
10. ,
在 的延长线上截取 ,
证 .
11. ,,,
.
,.
.
在 和 中,
.
.
12. 如图所示,在山前空地选取一个可以直接到达隧道两端 , 的一点 ,连接 并延长到点 ,使 ;连接 并延长到点 ,使 ,连接 ,并测出 的长度,则 的长度就是 , 间的距离.
理由如下:
在 和 中,
,,,
.
.
13. ,
,即 ,
在 和 中,
.
14. (1) 画法不唯一,如图所示.
(2) ,
,
,
,
,
,
,
,,
,
在 和 中,
.
第1页(共1 页)
