人教版八上-第十二章 全等三角形-12.1 全等三角形(word版含答案)
文档属性
| 名称 | 人教版八上-第十二章 全等三角形-12.1 全等三角形(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览

文档简介
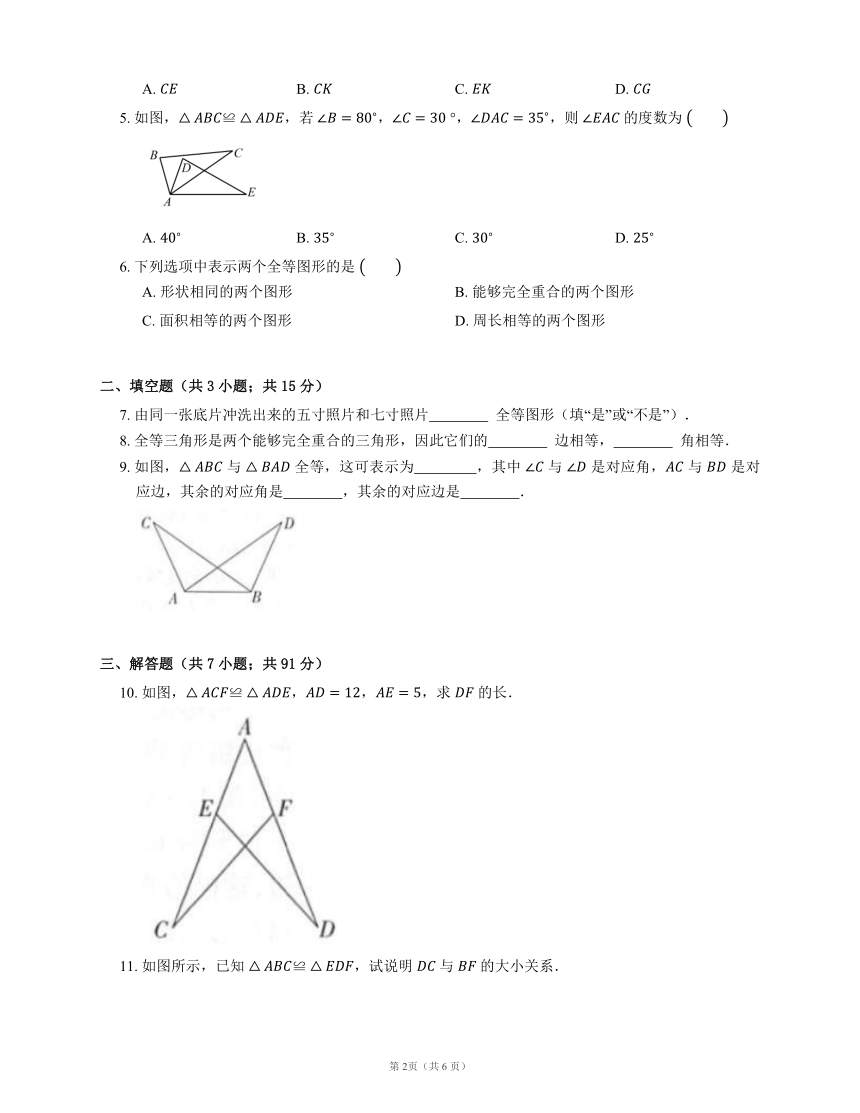
八上-第十二章 全等三角形-12.1 全等三角形
一、选择题(共6小题;共30分)
1. 如图,,,则下列结论中,错误的是
A. B.
C. D.
2. 如图,若 ,则下列结论中一定成立的是
A. B.
C. D.
3. 下列各组的两个图形属于全等图形的是
A. B.
C. D.
4. 已知 ,则 的对应边为
A. B. C. D.
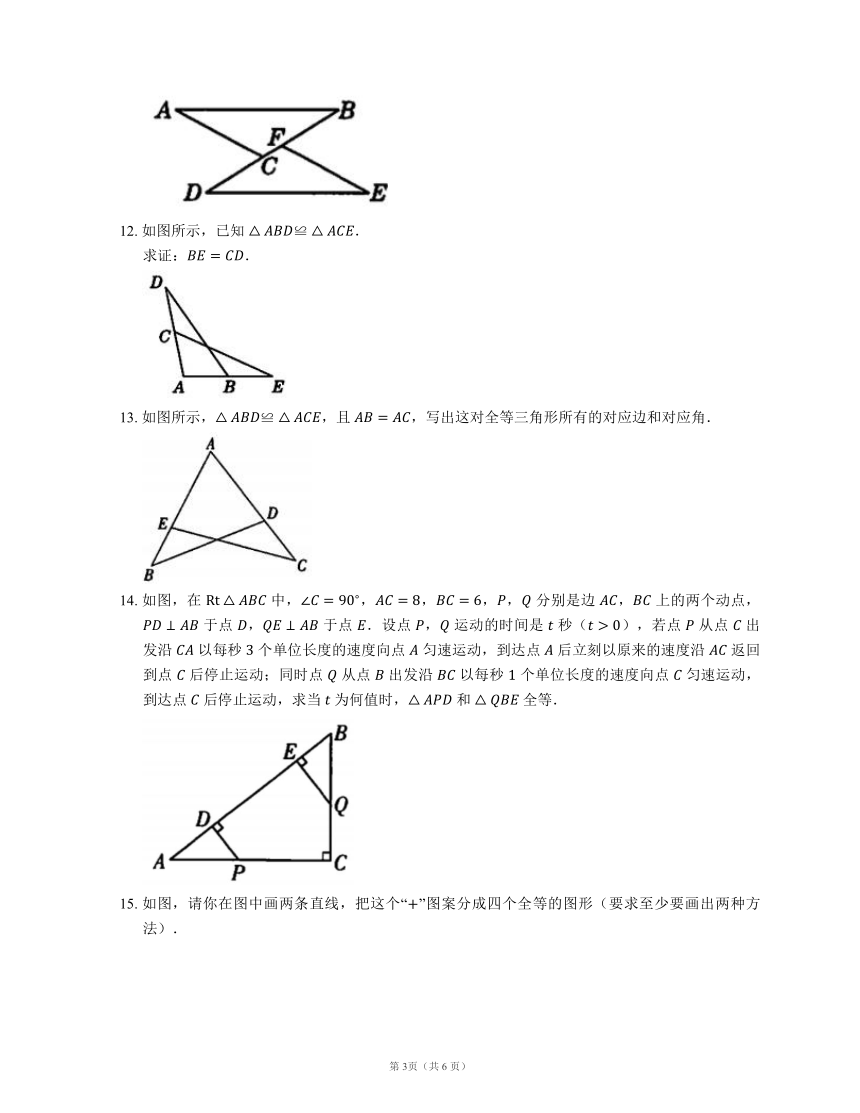
5. 如图,,若 , °,,则 的度数为
A. B. C. D.
6. 下列选项中表示两个全等图形的是
A. 形状相同的两个图形 B. 能够完全重合的两个图形
C. 面积相等的两个图形 D. 周长相等的两个图形
二、填空题(共3小题;共15分)
7. 由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”).
8. 全等三角形是两个能够完全重合的三角形,因此它们的 边相等, 角相等.
9. 如图, 与 全等,这可表示为 ,其中 与 是对应角, 与 是对应边,其余的对应角是 ,其余的对应边是 .
三、解答题(共7小题;共91分)
10. 如图,,,,求 的长.
11. 如图所示,已知 ,试说明 与 的大小关系.
12. 如图所示,已知 .
求证:.
13. 如图所示,,且 ,写出这对全等三角形所有的对应边和对应角.
14. 如图,在 中,,,,, 分别是边 , 上的两个动点, 于点 , 于点 .设点 , 运动的时间是 秒(),若点 从点 出发沿 以每秒 个单位长度的速度向点 匀速运动,到达点 后立刻以原来的速度沿 返回到点 后停止运动;同时点 从点 出发沿 以每秒 个单位长度的速度向点 匀速运动,到达点 后停止运动,求当 为何值时, 和 全等.
15. 如图,请你在图中画两条直线,把这个“”图案分成四个全等的图形(要求至少要画出两种方法).
16. 如图,已知 ,,.
(1)求证:;
(2)求 的长.
答案
第一部分
1. C
2. A 【解析】A、 ,
,
,
即 ,本选项结论成立;
B、 ,
,而 与 不一定相等,本选项结论不成立;
C、 ,
,而 与 不一定相等,本选项结论不成立;
D、 ,
,而 与 不一定相等,本选项结论不成立;
故选:A.
3. D 【解析】A中两个嘴巴不能完全重合,故本选项错误;
B中两个正方形边长不相等,不能完全重合,故本选项错误;
C中圆内两条相交的线段不能完全重合,故本选项错误;
D中两个图形能完全重合,故本选项正确.
4. B 【解析】题目给出明确的全等等式时,我们通常根据等式中的字母的对应位置确定三角形的对应顶点,进而判断边和角的对应关系,因此观察“”得, 的对应边为 .
5. B
6. B 【解析】A、形状相同的两个图形,不一定是全等图形,故此选项错误;
B、能够完全重合的两个图形,一定是全等图形,故此选项正确;
C、面积相等的两个图形,不一定是全等图形,故此选项错误;
D、周长相等的两个图形,不一定是全等图形,故此选项错误;
故选:B.
第二部分
7. 不是
8. 对应,对应
9. , 与 , 与 , 与 , 与
第三部分
10. ,,
,
,
.
11. ,
.
,
即 .
12. ,
,,
,即 .
13. 对应边: 与 , 与 , 与 ;
对应角: 与 , 与 , 与 .
14. ,,
.
①当 时,,.
和 全等,
,即 .解得 .
②当 时,,.
和 全等,
,即 .解得 .
综上所述,当 时, 和 全等.
15. 如图所示(答案不唯一).
16. (1) ,
.
.
(2) ,
.
,即 .
,,
.
.
.
第1页(共1 页)
一、选择题(共6小题;共30分)
1. 如图,,,则下列结论中,错误的是
A. B.
C. D.
2. 如图,若 ,则下列结论中一定成立的是
A. B.
C. D.
3. 下列各组的两个图形属于全等图形的是
A. B.
C. D.
4. 已知 ,则 的对应边为
A. B. C. D.
5. 如图,,若 , °,,则 的度数为
A. B. C. D.
6. 下列选项中表示两个全等图形的是
A. 形状相同的两个图形 B. 能够完全重合的两个图形
C. 面积相等的两个图形 D. 周长相等的两个图形
二、填空题(共3小题;共15分)
7. 由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”).
8. 全等三角形是两个能够完全重合的三角形,因此它们的 边相等, 角相等.
9. 如图, 与 全等,这可表示为 ,其中 与 是对应角, 与 是对应边,其余的对应角是 ,其余的对应边是 .
三、解答题(共7小题;共91分)
10. 如图,,,,求 的长.
11. 如图所示,已知 ,试说明 与 的大小关系.
12. 如图所示,已知 .
求证:.
13. 如图所示,,且 ,写出这对全等三角形所有的对应边和对应角.
14. 如图,在 中,,,,, 分别是边 , 上的两个动点, 于点 , 于点 .设点 , 运动的时间是 秒(),若点 从点 出发沿 以每秒 个单位长度的速度向点 匀速运动,到达点 后立刻以原来的速度沿 返回到点 后停止运动;同时点 从点 出发沿 以每秒 个单位长度的速度向点 匀速运动,到达点 后停止运动,求当 为何值时, 和 全等.
15. 如图,请你在图中画两条直线,把这个“”图案分成四个全等的图形(要求至少要画出两种方法).
16. 如图,已知 ,,.
(1)求证:;
(2)求 的长.
答案
第一部分
1. C
2. A 【解析】A、 ,
,
,
即 ,本选项结论成立;
B、 ,
,而 与 不一定相等,本选项结论不成立;
C、 ,
,而 与 不一定相等,本选项结论不成立;
D、 ,
,而 与 不一定相等,本选项结论不成立;
故选:A.
3. D 【解析】A中两个嘴巴不能完全重合,故本选项错误;
B中两个正方形边长不相等,不能完全重合,故本选项错误;
C中圆内两条相交的线段不能完全重合,故本选项错误;
D中两个图形能完全重合,故本选项正确.
4. B 【解析】题目给出明确的全等等式时,我们通常根据等式中的字母的对应位置确定三角形的对应顶点,进而判断边和角的对应关系,因此观察“”得, 的对应边为 .
5. B
6. B 【解析】A、形状相同的两个图形,不一定是全等图形,故此选项错误;
B、能够完全重合的两个图形,一定是全等图形,故此选项正确;
C、面积相等的两个图形,不一定是全等图形,故此选项错误;
D、周长相等的两个图形,不一定是全等图形,故此选项错误;
故选:B.
第二部分
7. 不是
8. 对应,对应
9. , 与 , 与 , 与 , 与
第三部分
10. ,,
,
,
.
11. ,
.
,
即 .
12. ,
,,
,即 .
13. 对应边: 与 , 与 , 与 ;
对应角: 与 , 与 , 与 .
14. ,,
.
①当 时,,.
和 全等,
,即 .解得 .
②当 时,,.
和 全等,
,即 .解得 .
综上所述,当 时, 和 全等.
15. 如图所示(答案不唯一).
16. (1) ,
.
.
(2) ,
.
,即 .
,,
.
.
.
第1页(共1 页)
