八上人教版 11.1.2 三角形的高、中线与角平分线
文档属性
| 名称 | 八上人教版 11.1.2 三角形的高、中线与角平分线 |
|
|
| 格式 | docx | ||
| 文件大小 | 492.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览


文档简介
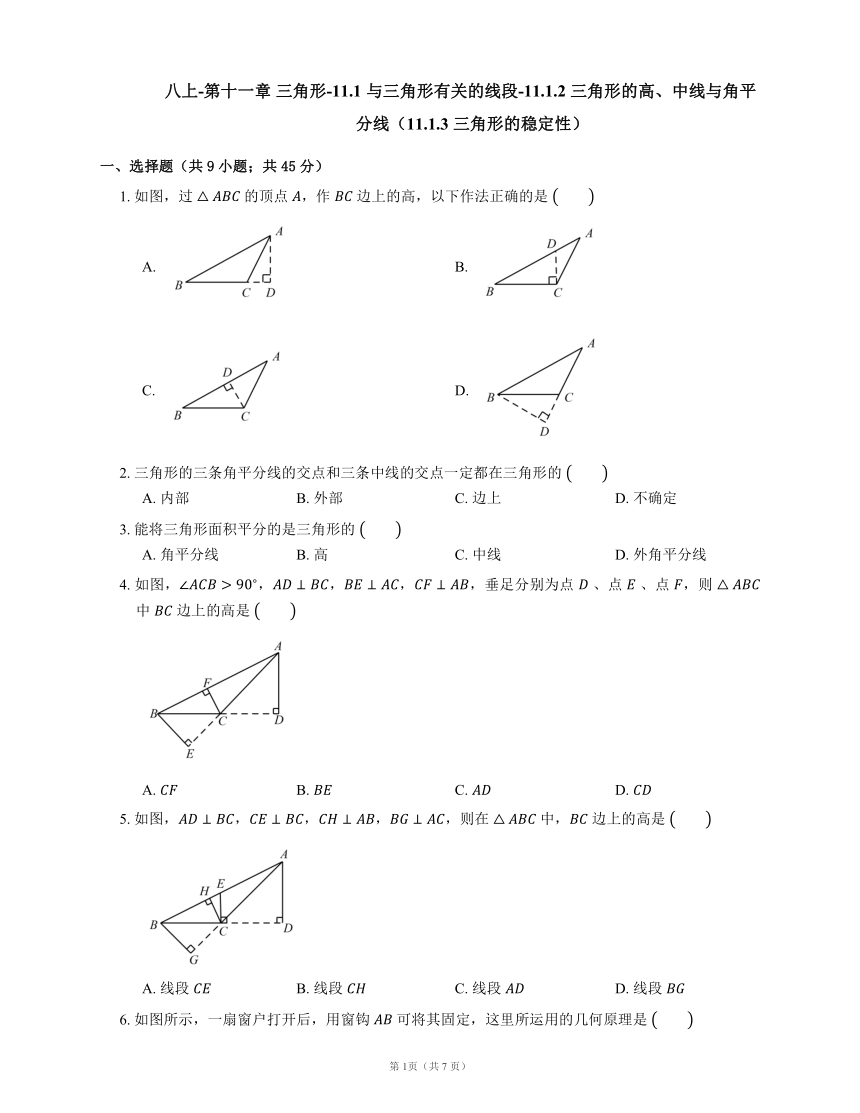
八上-第十一章 三角形-11.1 与三角形有关的线段-11.1.2 三角形的高、中线与角平分线(11.1.3 三角形的稳定性)
一、选择题(共9小题;共45分)
1. 如图,过 的顶点 ,作 边上的高,以下作法正确的是
A. B.
C. D.
2. 三角形的三条角平分线的交点和三条中线的交点一定都在三角形的
A. 内部 B. 外部 C. 边上 D. 不确定
3. 能将三角形面积平分的是三角形的
A. 角平分线 B. 高 C. 中线 D. 外角平分线
4. 如图,,,,,垂足分别为点 、点 、点 ,则 中 边上的高是
A. B. C. D.
5. 如图,,,,,则在 中, 边上的高是
A. 线段 B. 线段 C. 线段 D. 线段
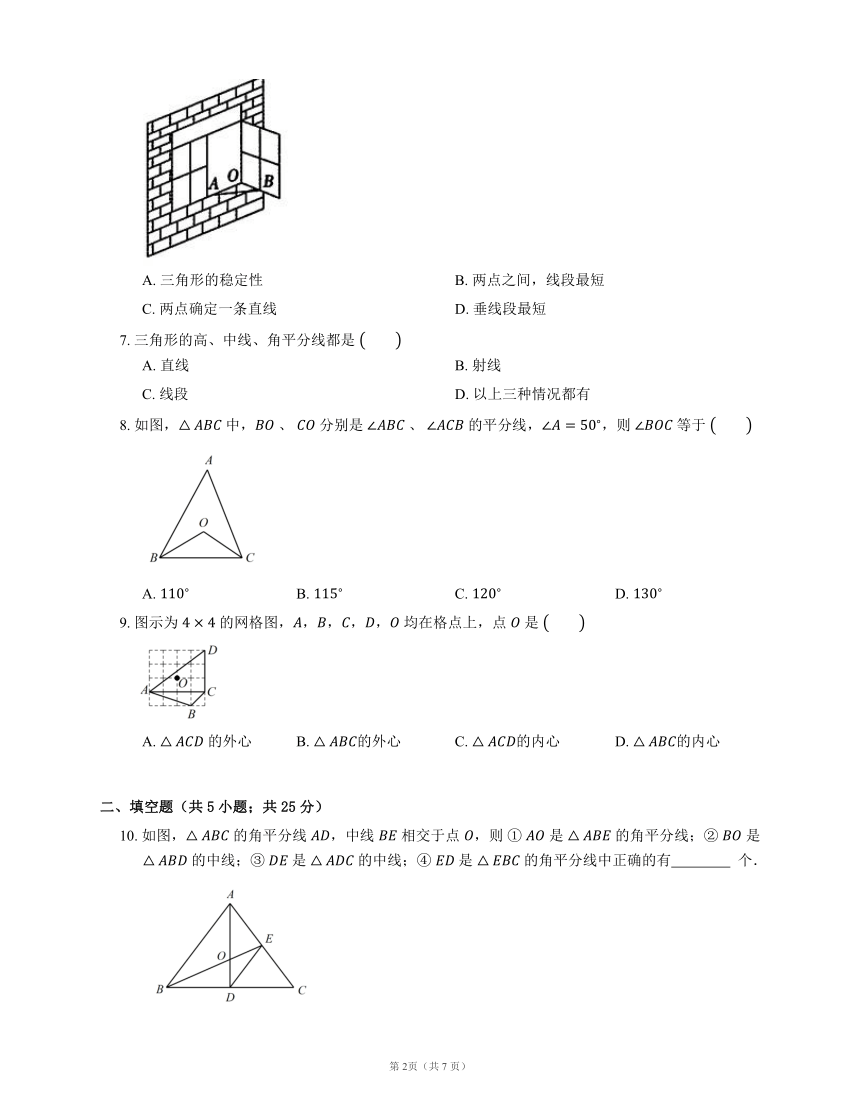
6. 如图所示,一扇窗户打开后,用窗钩 可将其固定,这里所运用的几何原理是
A. 三角形的稳定性 B. 两点之间,线段最短
C. 两点确定一条直线 D. 垂线段最短
7. 三角形的高、中线、角平分线都是
A. 直线 B. 射线
C. 线段 D. 以上三种情况都有
8. 如图, 中, 、 分别是 、 的平分线,,则 等于
A. B. C. D.
9. 图示为 的网格图,,,,, 均在格点上,点 是
A. 的外心 B. C. D.
二、填空题(共5小题;共25分)
10. 如图, 的角平分线 ,中线 相交于点 ,则 ① 是 的角平分线;② 是 的中线;③ 是 的中线;④ 是 的角平分线中正确的有 个.
11. 如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
12. 如图,在 中,,三角形的外角 和 的平分线交于点 ,则 .
13. 如图,在 中,,, 分别平分 ,, 与 相交于点 ,,,,,则 .
14. 如图所示,线段 , 分别是 的中线和高线,且 ,.
① 与 的周长的差为 ;
② 与 的面积关系为 .
三、解答题(共5小题;共65分)
15. 已知 (如图).
(1)作 边上的中线.
(2)作 的平分线.
(3)作 边上的高线.
16. 如图,在钝角 中.
(1)作钝角 的高 ,;
(2)若 ,,求 与 之比.
17. 如图,已知 , 分别是 的中线和高, 的周长比 的周长大 ,且 ,求 的长及 与 的面积之间的关系.
18. 在 中, 是 边的中点,, 把 的周长分成了 和 两部分,求这个三角形各边的长度.
19. 在 中,, 边上的中线 把 的周长分为 和 两个部分,求 的三边长·
答案
第一部分
1. A 【解析】为 中 边上的高的是A选项.
2. A
3. C
4. C
5. C
6. A 【解析】用窗钩 固定后,可形成 ,三角形具有稳定性,所以边 能被固定住,故选A.
7. C
8. B
9. B 【解析】提示:.
第二部分
10.
11. 三角形的稳定性
12.
【解析】因为 ,
所以 .
所以 .
因为 平分 , 平分 ,
所以 .
所以 .
13.
14. ,相等
第三部分
15. 如图 ,, 即为所求.
16. (1) 如图,, 为所作;
(2) 因为 , 为 的高,
所以 ,
所以 .
17. 的周长 ,
的周长 ,
,
又 ,
,
又 ,
,
,
,
,
,
.
18. 设 ,则
当 时,则
这时有 ,
所以 ,
因此
此时有
故不能组成三角形,这种情况不存在;
当 时,则
这时有 ,
所以 ,
故
符合三角形三边关系
所以这个三角形的三边长分别为 ,,.
19. 设 , ,
则 , .
由题意知 或
解得 或
所以 的三边长为 ,, 或 ,, .
第1页(共1 页)
一、选择题(共9小题;共45分)
1. 如图,过 的顶点 ,作 边上的高,以下作法正确的是
A. B.
C. D.
2. 三角形的三条角平分线的交点和三条中线的交点一定都在三角形的
A. 内部 B. 外部 C. 边上 D. 不确定
3. 能将三角形面积平分的是三角形的
A. 角平分线 B. 高 C. 中线 D. 外角平分线
4. 如图,,,,,垂足分别为点 、点 、点 ,则 中 边上的高是
A. B. C. D.
5. 如图,,,,,则在 中, 边上的高是
A. 线段 B. 线段 C. 线段 D. 线段
6. 如图所示,一扇窗户打开后,用窗钩 可将其固定,这里所运用的几何原理是
A. 三角形的稳定性 B. 两点之间,线段最短
C. 两点确定一条直线 D. 垂线段最短
7. 三角形的高、中线、角平分线都是
A. 直线 B. 射线
C. 线段 D. 以上三种情况都有
8. 如图, 中, 、 分别是 、 的平分线,,则 等于
A. B. C. D.
9. 图示为 的网格图,,,,, 均在格点上,点 是
A. 的外心 B. C. D.
二、填空题(共5小题;共25分)
10. 如图, 的角平分线 ,中线 相交于点 ,则 ① 是 的角平分线;② 是 的中线;③ 是 的中线;④ 是 的角平分线中正确的有 个.
11. 如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
12. 如图,在 中,,三角形的外角 和 的平分线交于点 ,则 .
13. 如图,在 中,,, 分别平分 ,, 与 相交于点 ,,,,,则 .
14. 如图所示,线段 , 分别是 的中线和高线,且 ,.
① 与 的周长的差为 ;
② 与 的面积关系为 .
三、解答题(共5小题;共65分)
15. 已知 (如图).
(1)作 边上的中线.
(2)作 的平分线.
(3)作 边上的高线.
16. 如图,在钝角 中.
(1)作钝角 的高 ,;
(2)若 ,,求 与 之比.
17. 如图,已知 , 分别是 的中线和高, 的周长比 的周长大 ,且 ,求 的长及 与 的面积之间的关系.
18. 在 中, 是 边的中点,, 把 的周长分成了 和 两部分,求这个三角形各边的长度.
19. 在 中,, 边上的中线 把 的周长分为 和 两个部分,求 的三边长·
答案
第一部分
1. A 【解析】为 中 边上的高的是A选项.
2. A
3. C
4. C
5. C
6. A 【解析】用窗钩 固定后,可形成 ,三角形具有稳定性,所以边 能被固定住,故选A.
7. C
8. B
9. B 【解析】提示:.
第二部分
10.
11. 三角形的稳定性
12.
【解析】因为 ,
所以 .
所以 .
因为 平分 , 平分 ,
所以 .
所以 .
13.
14. ,相等
第三部分
15. 如图 ,, 即为所求.
16. (1) 如图,, 为所作;
(2) 因为 , 为 的高,
所以 ,
所以 .
17. 的周长 ,
的周长 ,
,
又 ,
,
又 ,
,
,
,
,
,
.
18. 设 ,则
当 时,则
这时有 ,
所以 ,
因此
此时有
故不能组成三角形,这种情况不存在;
当 时,则
这时有 ,
所以 ,
故
符合三角形三边关系
所以这个三角形的三边长分别为 ,,.
19. 设 , ,
则 , .
由题意知 或
解得 或
所以 的三边长为 ,, 或 ,, .
第1页(共1 页)
