人教版八上-第十一章 三角形-11.3 多边形及其内角和-11.3.1 多边形(word版含答案)
文档属性
| 名称 | 人教版八上-第十一章 三角形-11.3 多边形及其内角和-11.3.1 多边形(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览

文档简介
八上-第十一章 三角形-11.3 多边形及其内角和-11.3.1 多边形
一、选择题(共10小题;共50分)
1. 过一个多边形的一个顶点可以引 条对角线,这个多边形是
A. 五边形 B. 七边形 C. 八边形 D. 六边形
2. 从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成几个三角形
A. B. C. D.
3. 若一个多边形从一个顶点可以引 条对角线,则它的边数是
A. B. C. D.
4. 从十二边形的一个顶点出发把一个多边形分成的三角形的个数是
A. B. C. D.
5. 从 边形的一个顶点出发共有对角线的条数是
A. B. C. D.
6. 若从一多边形的一个顶点出发,最多可引 条对角线,则它是
A. 十三边形 B. 十二边形 C. 十一边形 D. 十边形
7. 如图,其中是凸多边形的有
A. (2)(4) B. (1)(2)(3) C. (1)(2)(4) D. (3)(4)
8. 若从多边形的某一顶点出发只能画五条对角线,则它是
A. 六边形 B. 七边形 C. 八边形 D. 九边形
9. 多边形的一个顶点处的所有对角线把多边形分成了 个三角形,则经过这一点的对角线的条数是
A. B. C. D.
10. 过 边形的其中一个顶点有 条对角线,则 为
A. B. C. D.
二、填空题(共2小题;共10分)
11. 从一个 边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成 个三角形,则 的值是 .
12. 过 边形的一个顶点可作 条对角线,可将 边形分成 个三角形.
三、解答题(共6小题;共78分)
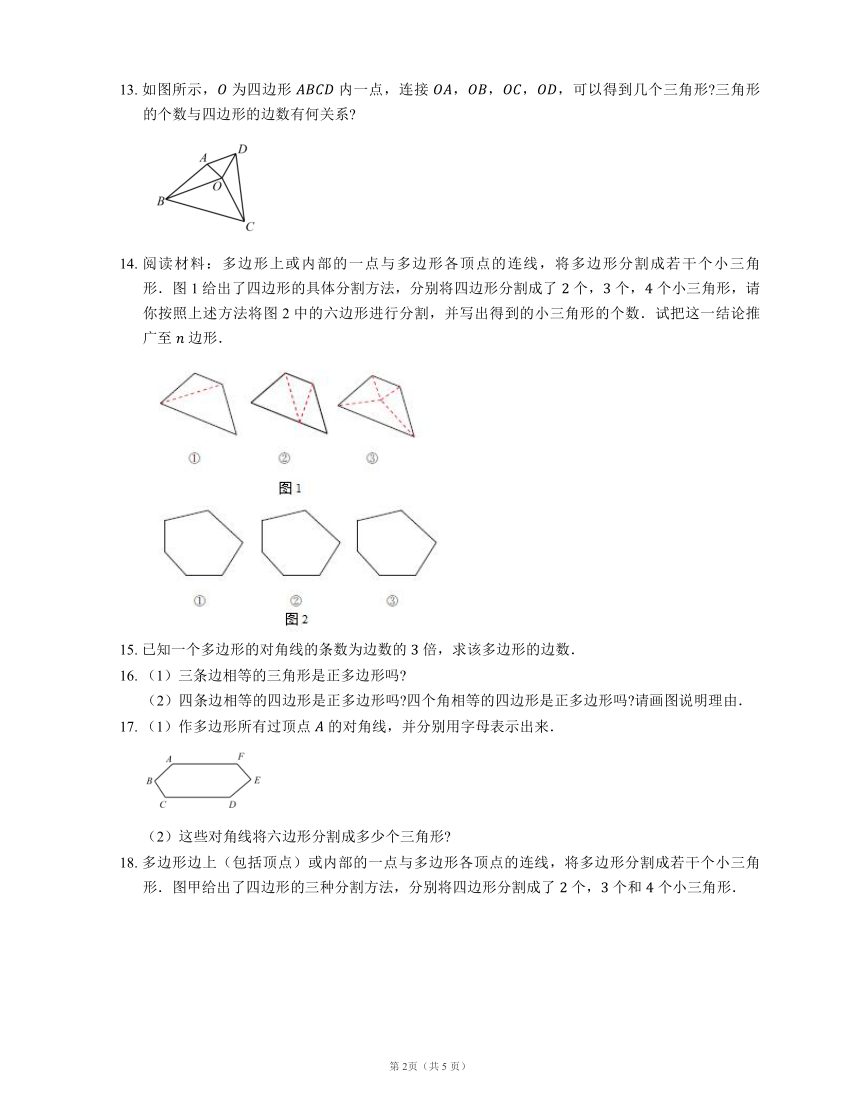
13. 如图所示, 为四边形 内一点,连接 ,,,,可以得到几个三角形 三角形的个数与四边形的边数有何关系
14. 阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图 1 给出了四边形的具体分割方法,分别将四边形分割成了 个, 个, 个小三角形,请你按照上述方法将图 2 中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至 边形.
15. 已知一个多边形的对角线的条数为边数的 倍,求该多边形的边数.
16. (1)三条边相等的三角形是正多边形吗
(2)四条边相等的四边形是正多边形吗 四个角相等的四边形是正多边形吗 请画图说明理由.
17. (1)作多边形所有过顶点 的对角线,并分别用字母表示出来.
(2)这些对角线将六边形分割成多少个三角形
18. 多边形边上(包括顶点)或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图甲给出了四边形的三种分割方法,分别将四边形分割成了 个, 个和 个小三角形.
(1)请你将图乙中的六边形按这三种方法分割,并写出得到的小三角形的个数.
(2)若将 边形 按这三种方法作类似的分割,所得的小三角形个数分别是多少
答案
第一部分
1. C 【解析】因为从 边形(, 为自然数)的一个顶点出发,可以引 条对角线,所以 ,所以 .
2. B
3. D
4. B
5. C
6. A 【解析】设这个多边形是 边形.依题意,得 ,
,故这个多边形是 边形.
7. C
8. C
9. C 【解析】设多边形有 条边,则 ,,设这个多边形为 边形, 边形上一个顶点处的对角线的条数是:.
10. D
【解析】 一个 边形过一个顶点有 条对角线,
,
解得 .
第二部分
11.
12. ,
第三部分
13. 可以得到 个三角形;三角形的个数与四边形的边数相等.
14. 如图所示.
第一种分割法可以把六边形分割成 个三角形,把 边形分割成 个三角形;
第二种分割法可以把六边形分割成 个三角形,把 边形分割成 个三角形;
第三种分割法可以把六边形分割成 个三角形,把 边形分割成 个三角形.
15. 设边数为 ,则 .
,则 ,解得 .
16. (1) 是.
(2) ①不一定,例如菱形四条边相等,但不一定是正多边形;
②不一定,长方形四个角都是直角,但不一定是正多边形.
17. (1) 如图,
,,.
(2) 个.
18. (1) 分割成三角形的个数分别为 个, 个, 个.
(2) 分割成的三角形个数分别为 个, 个, 个.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 过一个多边形的一个顶点可以引 条对角线,这个多边形是
A. 五边形 B. 七边形 C. 八边形 D. 六边形
2. 从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成几个三角形
A. B. C. D.
3. 若一个多边形从一个顶点可以引 条对角线,则它的边数是
A. B. C. D.
4. 从十二边形的一个顶点出发把一个多边形分成的三角形的个数是
A. B. C. D.
5. 从 边形的一个顶点出发共有对角线的条数是
A. B. C. D.
6. 若从一多边形的一个顶点出发,最多可引 条对角线,则它是
A. 十三边形 B. 十二边形 C. 十一边形 D. 十边形
7. 如图,其中是凸多边形的有
A. (2)(4) B. (1)(2)(3) C. (1)(2)(4) D. (3)(4)
8. 若从多边形的某一顶点出发只能画五条对角线,则它是
A. 六边形 B. 七边形 C. 八边形 D. 九边形
9. 多边形的一个顶点处的所有对角线把多边形分成了 个三角形,则经过这一点的对角线的条数是
A. B. C. D.
10. 过 边形的其中一个顶点有 条对角线,则 为
A. B. C. D.
二、填空题(共2小题;共10分)
11. 从一个 边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成 个三角形,则 的值是 .
12. 过 边形的一个顶点可作 条对角线,可将 边形分成 个三角形.
三、解答题(共6小题;共78分)
13. 如图所示, 为四边形 内一点,连接 ,,,,可以得到几个三角形 三角形的个数与四边形的边数有何关系
14. 阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图 1 给出了四边形的具体分割方法,分别将四边形分割成了 个, 个, 个小三角形,请你按照上述方法将图 2 中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至 边形.
15. 已知一个多边形的对角线的条数为边数的 倍,求该多边形的边数.
16. (1)三条边相等的三角形是正多边形吗
(2)四条边相等的四边形是正多边形吗 四个角相等的四边形是正多边形吗 请画图说明理由.
17. (1)作多边形所有过顶点 的对角线,并分别用字母表示出来.
(2)这些对角线将六边形分割成多少个三角形
18. 多边形边上(包括顶点)或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图甲给出了四边形的三种分割方法,分别将四边形分割成了 个, 个和 个小三角形.
(1)请你将图乙中的六边形按这三种方法分割,并写出得到的小三角形的个数.
(2)若将 边形 按这三种方法作类似的分割,所得的小三角形个数分别是多少
答案
第一部分
1. C 【解析】因为从 边形(, 为自然数)的一个顶点出发,可以引 条对角线,所以 ,所以 .
2. B
3. D
4. B
5. C
6. A 【解析】设这个多边形是 边形.依题意,得 ,
,故这个多边形是 边形.
7. C
8. C
9. C 【解析】设多边形有 条边,则 ,,设这个多边形为 边形, 边形上一个顶点处的对角线的条数是:.
10. D
【解析】 一个 边形过一个顶点有 条对角线,
,
解得 .
第二部分
11.
12. ,
第三部分
13. 可以得到 个三角形;三角形的个数与四边形的边数相等.
14. 如图所示.
第一种分割法可以把六边形分割成 个三角形,把 边形分割成 个三角形;
第二种分割法可以把六边形分割成 个三角形,把 边形分割成 个三角形;
第三种分割法可以把六边形分割成 个三角形,把 边形分割成 个三角形.
15. 设边数为 ,则 .
,则 ,解得 .
16. (1) 是.
(2) ①不一定,例如菱形四条边相等,但不一定是正多边形;
②不一定,长方形四个角都是直角,但不一定是正多边形.
17. (1) 如图,
,,.
(2) 个.
18. (1) 分割成三角形的个数分别为 个, 个, 个.
(2) 分割成的三角形个数分别为 个, 个, 个.
第1页(共1 页)
