人教版八上-第十一章 三角形11.3.2 多边形的内角和(word版含答案)
文档属性
| 名称 | 人教版八上-第十一章 三角形11.3.2 多边形的内角和(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 60.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 17:12:53 | ||
图片预览

文档简介
八上-第十一章 三角形-11.3 多边形及其内角和-11.3.2 多边形的内角和
一、选择题(共8小题;共40分)
1. 如图所示,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 的新多边形,则原多边形的边数为
A. B. C. D.
2. 正 边形的每个内角都是 ,则 的值是
A. B. C. D.
3. 一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为 ,则原多边形的边数为
A. B. C. D. 或
4. 若一个多边形的边数增加 ,则它的内角和
A. 不变 B. 是 C. 增加 D. 增加
5. 一个多边形的内角和是外角和的 倍,则这个多边形的边数为
A. B. C. D.
6. 若一个多边形的每个内角都等于 ,则这个多边形的边数是
A. B. C. D.
7. 一个多边形的内角和是 ,这个多边形的边数是
A. B. C. D.
8. 一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;共30分)
9. 边形的外角和是 .
10. 如果一个多边形的每个外角都是 ,那么这个多边形的内角和的度数为 .
11. 八边形的内角和是 度.
12. 如果一个正多边形的内角和等于 ,那么该正多边形的一个外角等于 度.
13. 一个多边形的内角和等于 ,这个多边形是 边形.
14. 十边形的外角和是
三、解答题(共6小题;共78分)
15. 如果一个多边形的每一个外角都等于 度,那么这个多边形的内角和是多少度
16. 已知一个多边形的每一个内角都是 ,它是几边形
17. 已知一个 边形的每一个内角都等于 .
(1)求 ;
(2)求这个 边形的内角和.
18. 已知一个多边形的内角和是 ,求这个多边形的对角线的条数.
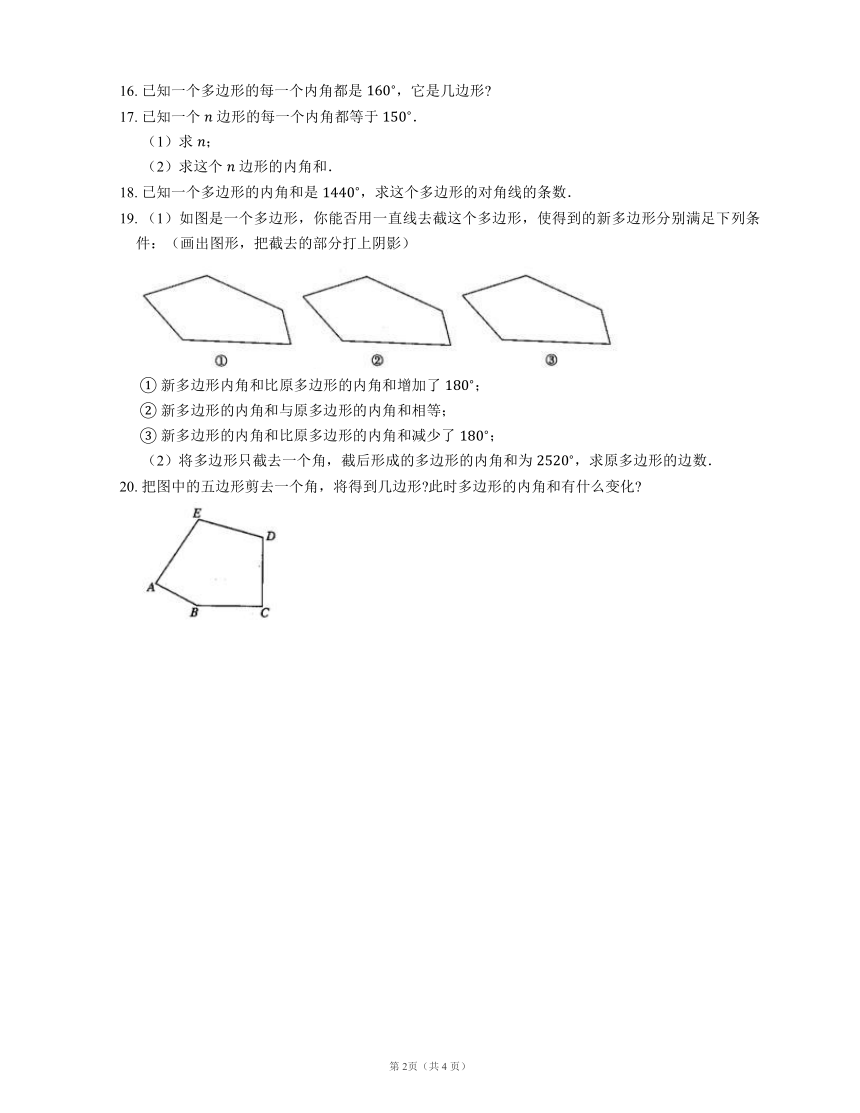
19. (1)如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:(画出图形,把截去的部分打上阴影)
新多边形内角和比原多边形的内角和增加了 ;
新多边形的内角和与原多边形的内角和相等;
新多边形的内角和比原多边形的内角和减少了 ;
(2)将多边形只截去一个角,截后形成的多边形的内角和为 ,求原多边形的边数.
20. 把图中的五边形剪去一个角,将得到几边形 此时多边形的内角和有什么变化
答案
第一部分
1. B 【解析】设新多边形是 边形,则由多边形内角和公式得 ,解得 ,
所以原多边形的边数是 .
2. C
3. B
4. C
5. C
6. C 【解析】由题意可得:,
解得 .
故多边形是 边形.
故选C.
7. C 【解析】根据内角和定理 即可求得.
8. C
第二部分
9.
【解析】 边形的外角和是 .
故答案为:.
10.
11.
12.
13. 八
14.
第三部分
15. 多边形每一个外角都等于 ,
它的边数为:,
它的内角和:.
故这个多边形的内角和是:.
16. 多边形的每一个内角都等于 ,
多边形的每一个外角都等于 ,
边数 .
该图形为十八边形.
17. (1) 每一个内角都等于 ,
每一个外角都等于 ,
边数 .
(2) 内角和:.
18. 因为 ,
所以 ,
所以 .
所以对角线的条数为 .
19. (1) 如图所示:
(2) 设新多边形的边数为 ,
则 ,解得 ,
若截去一个角后边数增加 ,则原多边形边数为 ,
若截去一个角后边数不变,则原多边形边数为 ,
若截去一个角后边数减少 ,则原多边形边数为 ,
故原多边形的边数可以为 , 或 .
20. 分三种情况:
()剪去一个角后为六边形,内角和为 ,内角和增加 ;
()剪去一个角后为四边形,内角和为 ,内角和减少 .
()剪去一个角后为五边形,内角和为 ,内角和不变.
第1页(共1 页)
一、选择题(共8小题;共40分)
1. 如图所示,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 的新多边形,则原多边形的边数为
A. B. C. D.
2. 正 边形的每个内角都是 ,则 的值是
A. B. C. D.
3. 一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为 ,则原多边形的边数为
A. B. C. D. 或
4. 若一个多边形的边数增加 ,则它的内角和
A. 不变 B. 是 C. 增加 D. 增加
5. 一个多边形的内角和是外角和的 倍,则这个多边形的边数为
A. B. C. D.
6. 若一个多边形的每个内角都等于 ,则这个多边形的边数是
A. B. C. D.
7. 一个多边形的内角和是 ,这个多边形的边数是
A. B. C. D.
8. 一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;共30分)
9. 边形的外角和是 .
10. 如果一个多边形的每个外角都是 ,那么这个多边形的内角和的度数为 .
11. 八边形的内角和是 度.
12. 如果一个正多边形的内角和等于 ,那么该正多边形的一个外角等于 度.
13. 一个多边形的内角和等于 ,这个多边形是 边形.
14. 十边形的外角和是
三、解答题(共6小题;共78分)
15. 如果一个多边形的每一个外角都等于 度,那么这个多边形的内角和是多少度
16. 已知一个多边形的每一个内角都是 ,它是几边形
17. 已知一个 边形的每一个内角都等于 .
(1)求 ;
(2)求这个 边形的内角和.
18. 已知一个多边形的内角和是 ,求这个多边形的对角线的条数.
19. (1)如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:(画出图形,把截去的部分打上阴影)
新多边形内角和比原多边形的内角和增加了 ;
新多边形的内角和与原多边形的内角和相等;
新多边形的内角和比原多边形的内角和减少了 ;
(2)将多边形只截去一个角,截后形成的多边形的内角和为 ,求原多边形的边数.
20. 把图中的五边形剪去一个角,将得到几边形 此时多边形的内角和有什么变化
答案
第一部分
1. B 【解析】设新多边形是 边形,则由多边形内角和公式得 ,解得 ,
所以原多边形的边数是 .
2. C
3. B
4. C
5. C
6. C 【解析】由题意可得:,
解得 .
故多边形是 边形.
故选C.
7. C 【解析】根据内角和定理 即可求得.
8. C
第二部分
9.
【解析】 边形的外角和是 .
故答案为:.
10.
11.
12.
13. 八
14.
第三部分
15. 多边形每一个外角都等于 ,
它的边数为:,
它的内角和:.
故这个多边形的内角和是:.
16. 多边形的每一个内角都等于 ,
多边形的每一个外角都等于 ,
边数 .
该图形为十八边形.
17. (1) 每一个内角都等于 ,
每一个外角都等于 ,
边数 .
(2) 内角和:.
18. 因为 ,
所以 ,
所以 .
所以对角线的条数为 .
19. (1) 如图所示:
(2) 设新多边形的边数为 ,
则 ,解得 ,
若截去一个角后边数增加 ,则原多边形边数为 ,
若截去一个角后边数不变,则原多边形边数为 ,
若截去一个角后边数减少 ,则原多边形边数为 ,
故原多边形的边数可以为 , 或 .
20. 分三种情况:
()剪去一个角后为六边形,内角和为 ,内角和增加 ;
()剪去一个角后为四边形,内角和为 ,内角和减少 .
()剪去一个角后为五边形,内角和为 ,内角和不变.
第1页(共1 页)
