人教A版选修2-3第一章 计数原理同步练习 1.1 分类加法计数原理与分步乘法计数原理(Word版,含解析)
文档属性
| 名称 | 人教A版选修2-3第一章 计数原理同步练习 1.1 分类加法计数原理与分步乘法计数原理(Word版,含解析) | 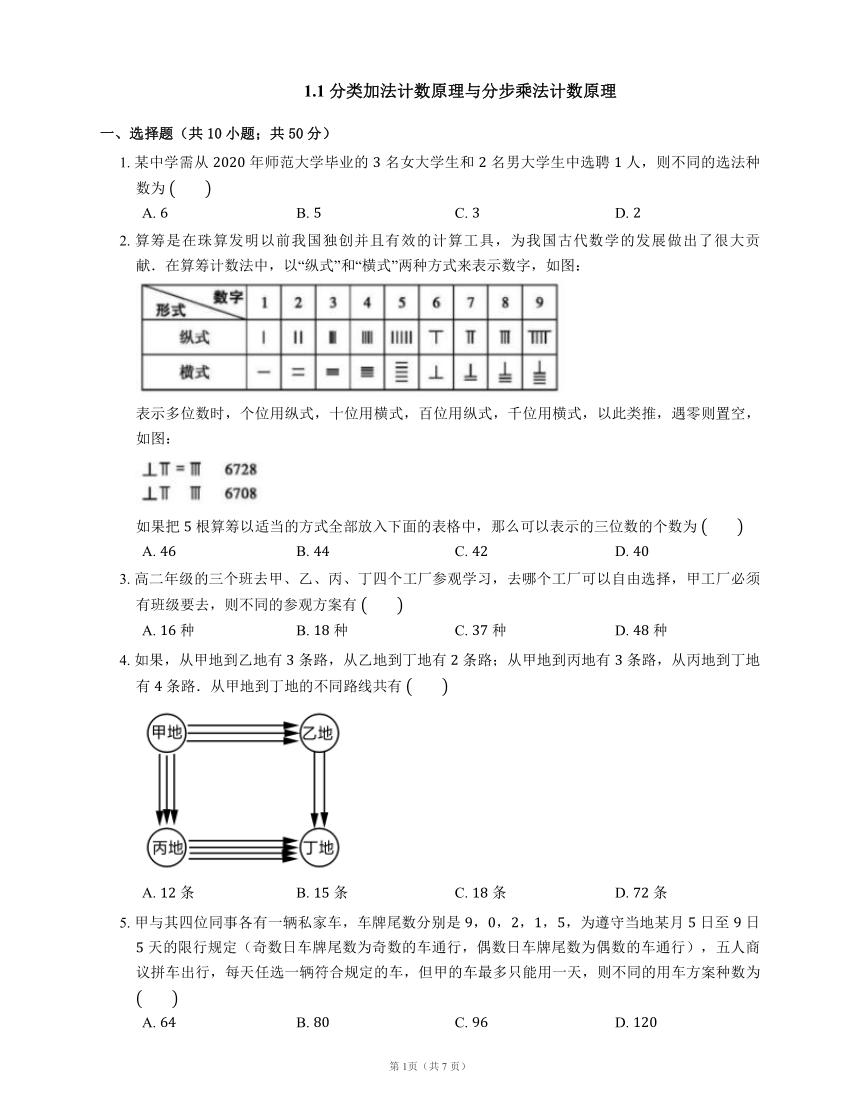 | |
| 格式 | docx | ||
| 文件大小 | 85.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 21:07:23 | ||
图片预览



文档简介
1.1 分类加法计数原理与分步乘法计数原理
一、选择题(共10小题;共50分)
1. 某中学需从 年师范大学毕业的 名女大学生和 名男大学生中选聘 人,则不同的选法种数为
A. B. C. D.
2. 算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
如果把 根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为
A. B. C. D.
3. 高二年级的三个班去甲、乙、丙、丁四个工厂参观学习,去哪个工厂可以自由选择,甲工厂必须有班级要去,则不同的参观方案有
A. 种 B. 种 C. 种 D. 种
4. 如果,从甲地到乙地有 条路,从乙地到丁地有 条路;从甲地到丙地有 条路,从丙地到丁地有 条路.从甲地到丁地的不同路线共有
A. 条 B. 条 C. 条 D. 条
5. 甲与其四位同事各有一辆私家车,车牌尾数分别是 ,,,,,为遵守当地某月 日至 日 天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为
A. B. C. D.
6. 中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学都选取到喜欢的礼物,则不同的选法有
A. 种 B. 种 C. 种 D. 种
7. 从 , 中选一个数字,从 ,, 中选两个数字,组成无重复数字的三位数,其中奇数的个数为
A. B. C. D.
8. 李雷和韩梅梅两人都计划在国庆节的 天假期中,到“东亚文化之都 泉州”二日游,若他们不同一天出现在泉州,则他们出游的不同方案共有
A. 种 B. 种 C. 种 D. 种
9. 如果一个三位正整数如“”满足 ,且 ,则称这样的三位数为凸数(如 ,, 等),那么所有凸数的个数为
A. B. C. D.
10. 从数字 ,,,, 中取出 个数字(允许重复),组成三位数,各位数字之和等于 ,则这样的三位数的个数为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 有 本不同的数学书, 本不同的语文书, 本不同的英语书,从中任取两本不同类的书,共有 种不同的取法.
12. 如图,从 有 种不同的走法.
13. 现有 种不同的颜色给如图所示的几何体的五个顶点 ,,,, 涂色,要求同一条棱上的两个顶点颜色不能相同,则一共有 种涂法.
14. 用红,黄,蓝三种颜色去涂图中标号为 ,,, 的九宫格中的 个小正方形(如图),使得任意相邻(有公共边)的小正方形所涂颜色都不相同,且标号为“,,”的小正方形涂相同的颜色,则符合条件的所有涂法有 种.
15. 若给一个各边不等的凸五边形的各边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色,则不同的染色方法共有 种.
三、解答题(共3小题;共39分)
16. 某地政府召集 家企业的负责人开会,其中甲企业有 人到会,其余 家企业各有 人到会,会上有 人发言,则这 人来自 家不同企业的情况有多少种
17. 某人设计了一项单人游戏,规则如下:先将一棋子放在如图所示的正方形 (边长为 个单位)的顶点 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为 ,则棋子就按逆时针方向行走 个单位,一直循环下去.某人抛掷三次骰子后,棋子恰好又回到点 处的所有不同走法共有多少种
18. 假设今天是 月 日,某市未来六天的空气质量预报情况如下表所示.该市有甲、乙、丙三人计划在未来六天( 月 日 月 日)内选择一天出游,在①甲只选择空气质量为优的一天出游;②乙不选择 月 日出游;③丙不选择 月 日出游;④甲与乙不选择同一天出游这四个条件中任选其中三个,求这三人出游的不同方法数.
未来六天空气质量预报
答案
第一部分
1. B 【解析】选取的方法可分为两类:从 名女大学生中选聘 人,有 种选法;
从 名男大学生中选聘 人.有 种选法.
根据分类加法计数原理,不同的选法种数为 ,故选B.
2. B 【解析】按每一位算筹的根数分类一共有 种情况,如下:,,,,,,,,,,,,,,,
根以上的算筹可以表示两个数字,运用分步乘法计数原理,
则上述情况能表示的三位数字个数分别为:
,,,,,,,,,,,,,,,
根据分类加法计数原理, 根算筹能表示的三位数字个数为
.
3. C 【解析】根据题意,若不考虑限制条件,每个班级都有 种选择,共有 种情况,
其中工厂甲没有班级去,即每个班都选择了其他三个工厂,此时每个班级都有 种选择,共有 种方案;
则符合条件的有 种.
4. C 【解析】若经乙地,则有 条,
若经甲地,则有 条,
故共有 条.
5. B
【解析】 日至 日,日期尾数分别为 ,,,,,有 天是奇数日, 天是偶数日.第一步,安排偶数日出行,每天都有 种选择,共有 种;第二步,安排奇数日出行,分两类,第一类,选 天安排甲的车,另外 天安排其他车,有 种,第二类,不安排甲的车,每天都有 种选择,共有 种,共有 种.根据分步乘法计数原理,不同的用车方案种数为 .
6. B 【解析】①甲同学选择牛,乙有 种选择,丙有 种选择,选法有 (种);
②甲同学选择马,乙有 种选择,丙有 种选择,选法有 (种),
所有总共有 (种)选法.
7. B 【解析】分两类情况讨论:
第 类,奇偶奇,个位有 种选择,十位有 种选择,百位有 种选择,共有 (个)奇数;
第 类,偶奇奇,个位有 种选择,十位有 种选择,百位有 种选择,共有 (个)奇数.
根据分类加法计数原理知,共有 (个)奇数.
8. C 【解析】任意相邻两天组合一起,一共有 种情况,如①②,②③,③④,④⑤,⑤⑥,⑥⑦,若李雷选①②或⑥⑦,则韩梅梅有 种选择,若李雷选②③或③④或④⑤或⑤⑥,则韩梅梅有 种选择,故若他们不同一天出现在泉州,则他们出游的不同方案共有 (种).
9. A 【解析】若 ,则百位数字只能选 ,个位数字可选 或 ,“凸数”为 与 ,共 个.
若 ,则百位数字有两种选择,个位数字有三种选择,则“凸数”有 (个).
若 ,满足条件的“凸数”有 (个),
,
若 ,满足条件的“凸数”有 (个).
所以所有凸数有 (个).
10. C
【解析】从数字 ,,,, 中取出 个数字(允许重复),组成三位数,各位数字之和等于 ,可分为三类情况:
()当三个数为 ,, 时, 可以在个位、十位、百位,所以共有 个这样的三位数;
()当三个数为 ,, 时,共有 个这样的三位数;
()当三个数为 ,, 时,只有 个这样的三位数.
由分类加法计数原理可得,共有 个,即这样的三位数共有 个.
第二部分
11.
【解析】任取两本不同类的书分为三类:①取数学、语文各一本;②取语文、英语各一本;③取数学、英语各一本.在每一类中利用分步乘法计数原理,再利用分类加法计数原理即可.共有 种不同取法.
12.
【解析】分为两类,不过 点有 种方法,过 点有 种方法,共有 种方法.
13.
【解析】第 类:顶点 , 同色.顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,此时顶点 与顶点 同色,只有 种颜色可选,顶点 有 种颜色可供选择,不同的涂法有 种.
第 类:顶点 , 不同色.顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,此时顶点 与顶点 不同色,有 种颜色可选,顶点 有 种颜色可供选择,不同的涂法有 种.综上,不同的涂法共有 种.
14.
【解析】分三步:第一步,先给标号 ,, 的小正方形涂色,有 种涂法.
第二步,给标号 ,, 的小正方形涂色,又分两类:一是标号 与标号 ,, 涂色相同,则标号 , 各有 种涂法,共 种涂法;二是标号 与标号 ,, 涂色不同,则标号 有 种涂法,此时标号 , 只有 种涂法,共 种涂法.综上可知,标号 ,, 的小正方形的涂法有 种.
第三步,给标号 ,, 的小正方形涂色,显然跟标号 ,, 的小正方形涂色方法一样,也是 种.
根据分步乘法计数原理,符合条件的所有涂法有 种.
15.
【解析】方法一:
如图,染五条边总体分五步,染每一边为一步.
当染边 时有 种染法,则染边 有 种染法.
()当 与 同色时有 种染法,则 有 种, 有 种,此时染法总数为 (种).
()当 与 不同色时, 有 种,
①当 与 同色时, 有 种, 有 种;
②当 与 不同色时, 有 种, 有 种,则此时有 (种).
综合(),(),由分类加法计数原理,可得染法的种数为 种.
方法二:
通过分析可知,每种颜色至少要涂 次,至多只能涂 次,即有一色涂 次,剩余两种颜色各涂 次.一次的有 种涂法,涂 次的有 种涂法,故一共有 (种)涂法.
第三部分
16. 第一类,甲企业有 人发言,有 种情况,另两个发言人来自其余 家企业,有 种情况,由分步乘法计数原理知有 种情况;
第二类, 人全来自其余 家企业,有 种情况.
根据分类加法计数原理,共有 种情况.
17. 由题意知正方形 (边长为 个单位)的周长是 ,
抛掷三次骰子后,棋子恰好又回到点 处表示三次骰子的点数之和是 ,
点数中三个数字能够使得和为 的有
,,,
,,,
,,,
,,,
,,,
,,,共 种组合.
① ,,;,,;,, 这三种组合中,每一种又可以列出 种不同结果,所以有 种;
② ,,;,, 这两种组合中,每种有 种结果,所以有 种;
③组合 ,, 只有 种结果.
根据分类加法计数原理知,共有 种不同走法.
18. 若选择①②③,则三人出游的不同方法数 .
若选择①②④,则需分两类,第一类,若甲选择 月 日出游,则三人出游的不同方法数 ;第二类,若甲不选择 月 日出游,则三人出游的不同方法数 .故这三人出游的不同方法数 .
若选择①③④,则三人出游的不同方法数 .
若选择②③④,则三人出游的不同方法数 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 某中学需从 年师范大学毕业的 名女大学生和 名男大学生中选聘 人,则不同的选法种数为
A. B. C. D.
2. 算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
如果把 根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为
A. B. C. D.
3. 高二年级的三个班去甲、乙、丙、丁四个工厂参观学习,去哪个工厂可以自由选择,甲工厂必须有班级要去,则不同的参观方案有
A. 种 B. 种 C. 种 D. 种
4. 如果,从甲地到乙地有 条路,从乙地到丁地有 条路;从甲地到丙地有 条路,从丙地到丁地有 条路.从甲地到丁地的不同路线共有
A. 条 B. 条 C. 条 D. 条
5. 甲与其四位同事各有一辆私家车,车牌尾数分别是 ,,,,,为遵守当地某月 日至 日 天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为
A. B. C. D.
6. 中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学都选取到喜欢的礼物,则不同的选法有
A. 种 B. 种 C. 种 D. 种
7. 从 , 中选一个数字,从 ,, 中选两个数字,组成无重复数字的三位数,其中奇数的个数为
A. B. C. D.
8. 李雷和韩梅梅两人都计划在国庆节的 天假期中,到“东亚文化之都 泉州”二日游,若他们不同一天出现在泉州,则他们出游的不同方案共有
A. 种 B. 种 C. 种 D. 种
9. 如果一个三位正整数如“”满足 ,且 ,则称这样的三位数为凸数(如 ,, 等),那么所有凸数的个数为
A. B. C. D.
10. 从数字 ,,,, 中取出 个数字(允许重复),组成三位数,各位数字之和等于 ,则这样的三位数的个数为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 有 本不同的数学书, 本不同的语文书, 本不同的英语书,从中任取两本不同类的书,共有 种不同的取法.
12. 如图,从 有 种不同的走法.
13. 现有 种不同的颜色给如图所示的几何体的五个顶点 ,,,, 涂色,要求同一条棱上的两个顶点颜色不能相同,则一共有 种涂法.
14. 用红,黄,蓝三种颜色去涂图中标号为 ,,, 的九宫格中的 个小正方形(如图),使得任意相邻(有公共边)的小正方形所涂颜色都不相同,且标号为“,,”的小正方形涂相同的颜色,则符合条件的所有涂法有 种.
15. 若给一个各边不等的凸五边形的各边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色,则不同的染色方法共有 种.
三、解答题(共3小题;共39分)
16. 某地政府召集 家企业的负责人开会,其中甲企业有 人到会,其余 家企业各有 人到会,会上有 人发言,则这 人来自 家不同企业的情况有多少种
17. 某人设计了一项单人游戏,规则如下:先将一棋子放在如图所示的正方形 (边长为 个单位)的顶点 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为 ,则棋子就按逆时针方向行走 个单位,一直循环下去.某人抛掷三次骰子后,棋子恰好又回到点 处的所有不同走法共有多少种
18. 假设今天是 月 日,某市未来六天的空气质量预报情况如下表所示.该市有甲、乙、丙三人计划在未来六天( 月 日 月 日)内选择一天出游,在①甲只选择空气质量为优的一天出游;②乙不选择 月 日出游;③丙不选择 月 日出游;④甲与乙不选择同一天出游这四个条件中任选其中三个,求这三人出游的不同方法数.
未来六天空气质量预报
答案
第一部分
1. B 【解析】选取的方法可分为两类:从 名女大学生中选聘 人,有 种选法;
从 名男大学生中选聘 人.有 种选法.
根据分类加法计数原理,不同的选法种数为 ,故选B.
2. B 【解析】按每一位算筹的根数分类一共有 种情况,如下:,,,,,,,,,,,,,,,
根以上的算筹可以表示两个数字,运用分步乘法计数原理,
则上述情况能表示的三位数字个数分别为:
,,,,,,,,,,,,,,,
根据分类加法计数原理, 根算筹能表示的三位数字个数为
.
3. C 【解析】根据题意,若不考虑限制条件,每个班级都有 种选择,共有 种情况,
其中工厂甲没有班级去,即每个班都选择了其他三个工厂,此时每个班级都有 种选择,共有 种方案;
则符合条件的有 种.
4. C 【解析】若经乙地,则有 条,
若经甲地,则有 条,
故共有 条.
5. B
【解析】 日至 日,日期尾数分别为 ,,,,,有 天是奇数日, 天是偶数日.第一步,安排偶数日出行,每天都有 种选择,共有 种;第二步,安排奇数日出行,分两类,第一类,选 天安排甲的车,另外 天安排其他车,有 种,第二类,不安排甲的车,每天都有 种选择,共有 种,共有 种.根据分步乘法计数原理,不同的用车方案种数为 .
6. B 【解析】①甲同学选择牛,乙有 种选择,丙有 种选择,选法有 (种);
②甲同学选择马,乙有 种选择,丙有 种选择,选法有 (种),
所有总共有 (种)选法.
7. B 【解析】分两类情况讨论:
第 类,奇偶奇,个位有 种选择,十位有 种选择,百位有 种选择,共有 (个)奇数;
第 类,偶奇奇,个位有 种选择,十位有 种选择,百位有 种选择,共有 (个)奇数.
根据分类加法计数原理知,共有 (个)奇数.
8. C 【解析】任意相邻两天组合一起,一共有 种情况,如①②,②③,③④,④⑤,⑤⑥,⑥⑦,若李雷选①②或⑥⑦,则韩梅梅有 种选择,若李雷选②③或③④或④⑤或⑤⑥,则韩梅梅有 种选择,故若他们不同一天出现在泉州,则他们出游的不同方案共有 (种).
9. A 【解析】若 ,则百位数字只能选 ,个位数字可选 或 ,“凸数”为 与 ,共 个.
若 ,则百位数字有两种选择,个位数字有三种选择,则“凸数”有 (个).
若 ,满足条件的“凸数”有 (个),
,
若 ,满足条件的“凸数”有 (个).
所以所有凸数有 (个).
10. C
【解析】从数字 ,,,, 中取出 个数字(允许重复),组成三位数,各位数字之和等于 ,可分为三类情况:
()当三个数为 ,, 时, 可以在个位、十位、百位,所以共有 个这样的三位数;
()当三个数为 ,, 时,共有 个这样的三位数;
()当三个数为 ,, 时,只有 个这样的三位数.
由分类加法计数原理可得,共有 个,即这样的三位数共有 个.
第二部分
11.
【解析】任取两本不同类的书分为三类:①取数学、语文各一本;②取语文、英语各一本;③取数学、英语各一本.在每一类中利用分步乘法计数原理,再利用分类加法计数原理即可.共有 种不同取法.
12.
【解析】分为两类,不过 点有 种方法,过 点有 种方法,共有 种方法.
13.
【解析】第 类:顶点 , 同色.顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,此时顶点 与顶点 同色,只有 种颜色可选,顶点 有 种颜色可供选择,不同的涂法有 种.
第 类:顶点 , 不同色.顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,顶点 有 种颜色可供选择,此时顶点 与顶点 不同色,有 种颜色可选,顶点 有 种颜色可供选择,不同的涂法有 种.综上,不同的涂法共有 种.
14.
【解析】分三步:第一步,先给标号 ,, 的小正方形涂色,有 种涂法.
第二步,给标号 ,, 的小正方形涂色,又分两类:一是标号 与标号 ,, 涂色相同,则标号 , 各有 种涂法,共 种涂法;二是标号 与标号 ,, 涂色不同,则标号 有 种涂法,此时标号 , 只有 种涂法,共 种涂法.综上可知,标号 ,, 的小正方形的涂法有 种.
第三步,给标号 ,, 的小正方形涂色,显然跟标号 ,, 的小正方形涂色方法一样,也是 种.
根据分步乘法计数原理,符合条件的所有涂法有 种.
15.
【解析】方法一:
如图,染五条边总体分五步,染每一边为一步.
当染边 时有 种染法,则染边 有 种染法.
()当 与 同色时有 种染法,则 有 种, 有 种,此时染法总数为 (种).
()当 与 不同色时, 有 种,
①当 与 同色时, 有 种, 有 种;
②当 与 不同色时, 有 种, 有 种,则此时有 (种).
综合(),(),由分类加法计数原理,可得染法的种数为 种.
方法二:
通过分析可知,每种颜色至少要涂 次,至多只能涂 次,即有一色涂 次,剩余两种颜色各涂 次.一次的有 种涂法,涂 次的有 种涂法,故一共有 (种)涂法.
第三部分
16. 第一类,甲企业有 人发言,有 种情况,另两个发言人来自其余 家企业,有 种情况,由分步乘法计数原理知有 种情况;
第二类, 人全来自其余 家企业,有 种情况.
根据分类加法计数原理,共有 种情况.
17. 由题意知正方形 (边长为 个单位)的周长是 ,
抛掷三次骰子后,棋子恰好又回到点 处表示三次骰子的点数之和是 ,
点数中三个数字能够使得和为 的有
,,,
,,,
,,,
,,,
,,,
,,,共 种组合.
① ,,;,,;,, 这三种组合中,每一种又可以列出 种不同结果,所以有 种;
② ,,;,, 这两种组合中,每种有 种结果,所以有 种;
③组合 ,, 只有 种结果.
根据分类加法计数原理知,共有 种不同走法.
18. 若选择①②③,则三人出游的不同方法数 .
若选择①②④,则需分两类,第一类,若甲选择 月 日出游,则三人出游的不同方法数 ;第二类,若甲不选择 月 日出游,则三人出游的不同方法数 .故这三人出游的不同方法数 .
若选择①③④,则三人出游的不同方法数 .
若选择②③④,则三人出游的不同方法数 .
第1页(共1 页)
