数学广角—集合(课件) 数学三年级上册(共17张PPT)人教版
文档属性
| 名称 | 数学广角—集合(课件) 数学三年级上册(共17张PPT)人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 14:22:41 | ||
图片预览


文档简介
(共15张PPT)
数学广角—集合
光明小学定于下周五举行
三年级组趣味运动会。
每班选择6名同学参加跳绳比赛。
每班选择5名同学参加踢毽子比赛。
每班有多少人参加比赛
三年级1班
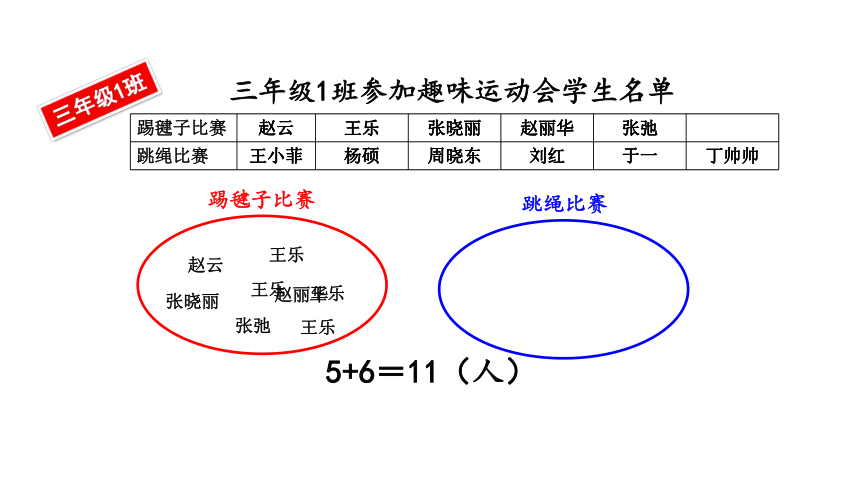
三年级1班参加趣味运动会学生名单
踢毽子比赛 赵云 王乐 张晓丽 赵丽华 张弛
跳绳比赛 王小菲 杨硕 周晓东 刘红 于一 丁帅帅
赵云
王乐
张晓丽
赵丽华
张弛
踢毽子比赛
跳绳比赛
王小菲
杨硕
周晓东
刘红
于一
丁帅帅
5+6=11(人)
赵云
王乐
张晓丽
赵丽华
张弛
王乐
王乐
王乐
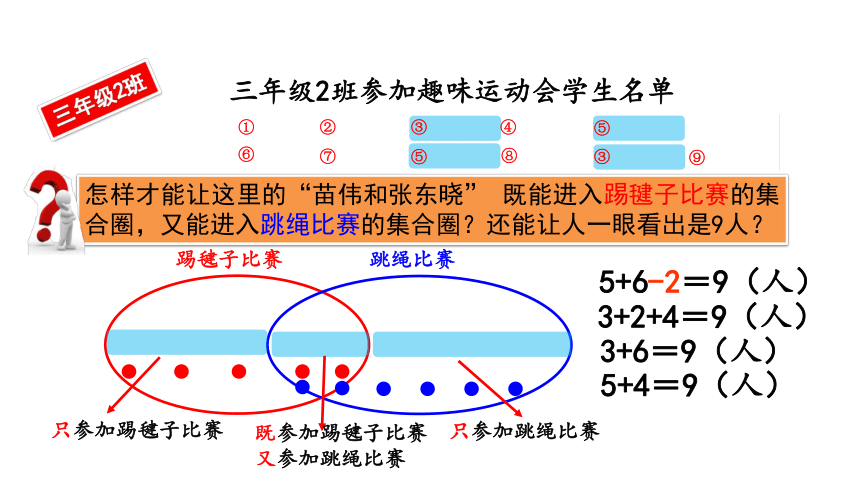
怎样才能让这里的“苗伟和张东晓” 既能进入踢毽子比赛的集合圈,又能进入跳绳比赛的集合圈?还能让人一眼看出是9人?
三年级2班
三年级2班参加趣味运动会学生名单
踢毽子比赛 张丽 王东 苗伟 赵星云 张东晓
跳绳比赛 王乐 杨云开 张东晓 刘梅 苗伟 刘纪丽
张丽
王东
赵星云
张东晓
踢毽子比赛
跳绳比赛
王乐
杨云开
张东晓
刘梅
苗伟
刘纪丽
5+6-2=9(人)
只参加踢毽子比赛
只参加跳绳比赛
既参加踢毽子比赛
又参加跳绳比赛
3+2+4=9(人)
3+6=9(人)
5+4=9(人)
①
②
③
④
⑤
⑥
⑦
⑧
⑤
③
⑨
三年级3班
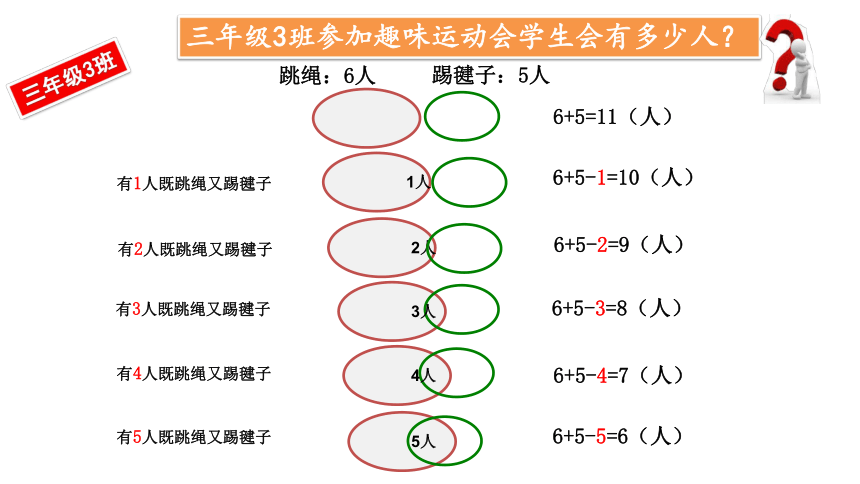
三年级3班参加趣味运动会学生会有多少人?
6+5=11(人)
6+5-1=10(人)
跳绳:6人
1人
2人
6+5-2=9(人)
3人
6+5-3=8(人)
4人
6+5-4=7(人)
踢毽子:5人
有1人既跳绳又踢毽子
有2人既跳绳又踢毽子
有3人既跳绳又踢毽子
有4人既跳绳又踢毽子
6+5-5=6(人)
5人
有5人既跳绳又踢毽子
6+5=11(人)
6+6-1=10(人)
跳绳:6人
1人
2人
6+5-2=9(人)
3人
6+5-3=8(人)
4人
6+5-4=7(人)
踢毽子:5人
有1人既跳绳又踢毽子
有2人既跳绳又踢毽子
有3人既跳绳又踢毽子
有4人既跳绳又踢毽子
5人
6+5-5=6(人)
有5人既跳绳又踢毽子
跳绳:a
踢毽:b
c
N
a
+
-
b
c
总数
两部分的和
-重叠部分
=
=
韦恩图
约翰.维恩(John Venn1834—1923)
十九世纪英国著名的哲学家、数学家、逻辑学家,他在前几代人研究的基础上于1881年发明了维恩图。
维恩图用于展示不同的事物群组(集合)之间的数学或逻辑联系,尤其适合用来表示集合间的关系,它也常常被用来帮助推导关于集合运算的一些规律。
你
知
道
吗
?
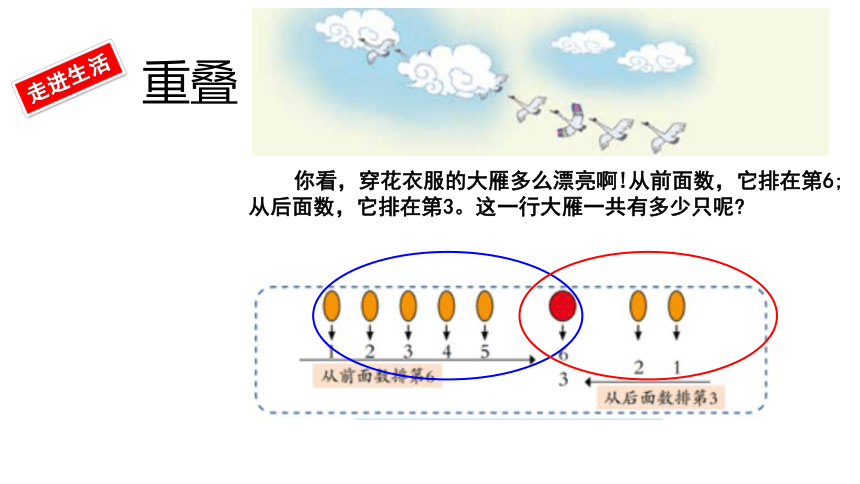
重叠
走进生活
你看,穿花衣服的大雁多么漂亮啊!从前面数,它排在第6;从后面数,它排在第3。这一行大雁一共有多少只呢
20cm
20cm
5cm
重叠
走进生活
在生活中会发现一些重叠问题。
创造维恩图,梳理重叠问题的数量关系。
数
形
结
合
借助维恩图,建立了数学模型。
运用维恩图的模型,解决问题。
吸烟的爸爸
喝酒的爸爸
既吸烟又喝酒的爸爸
既不吸烟又不喝酒的爸爸又该怎么表示呢?
进一步探索更深奥的重叠问题。
……
在生活中会发现一些重叠问题。
创造维恩图,梳理重叠问题的数量关系。
数
形
结
合
借助维恩图,建立了数学模型。
运用维恩图的模型,解决问题。
吸烟的爸爸
喝酒的爸爸
既吸烟又喝酒的爸爸
既不吸烟又不喝酒的爸爸又该怎么表示呢?
下
课
了
数学广角—集合
光明小学定于下周五举行
三年级组趣味运动会。
每班选择6名同学参加跳绳比赛。
每班选择5名同学参加踢毽子比赛。
每班有多少人参加比赛
三年级1班
三年级1班参加趣味运动会学生名单
踢毽子比赛 赵云 王乐 张晓丽 赵丽华 张弛
跳绳比赛 王小菲 杨硕 周晓东 刘红 于一 丁帅帅
赵云
王乐
张晓丽
赵丽华
张弛
踢毽子比赛
跳绳比赛
王小菲
杨硕
周晓东
刘红
于一
丁帅帅
5+6=11(人)
赵云
王乐
张晓丽
赵丽华
张弛
王乐
王乐
王乐
怎样才能让这里的“苗伟和张东晓” 既能进入踢毽子比赛的集合圈,又能进入跳绳比赛的集合圈?还能让人一眼看出是9人?
三年级2班
三年级2班参加趣味运动会学生名单
踢毽子比赛 张丽 王东 苗伟 赵星云 张东晓
跳绳比赛 王乐 杨云开 张东晓 刘梅 苗伟 刘纪丽
张丽
王东
赵星云
张东晓
踢毽子比赛
跳绳比赛
王乐
杨云开
张东晓
刘梅
苗伟
刘纪丽
5+6-2=9(人)
只参加踢毽子比赛
只参加跳绳比赛
既参加踢毽子比赛
又参加跳绳比赛
3+2+4=9(人)
3+6=9(人)
5+4=9(人)
①
②
③
④
⑤
⑥
⑦
⑧
⑤
③
⑨
三年级3班
三年级3班参加趣味运动会学生会有多少人?
6+5=11(人)
6+5-1=10(人)
跳绳:6人
1人
2人
6+5-2=9(人)
3人
6+5-3=8(人)
4人
6+5-4=7(人)
踢毽子:5人
有1人既跳绳又踢毽子
有2人既跳绳又踢毽子
有3人既跳绳又踢毽子
有4人既跳绳又踢毽子
6+5-5=6(人)
5人
有5人既跳绳又踢毽子
6+5=11(人)
6+6-1=10(人)
跳绳:6人
1人
2人
6+5-2=9(人)
3人
6+5-3=8(人)
4人
6+5-4=7(人)
踢毽子:5人
有1人既跳绳又踢毽子
有2人既跳绳又踢毽子
有3人既跳绳又踢毽子
有4人既跳绳又踢毽子
5人
6+5-5=6(人)
有5人既跳绳又踢毽子
跳绳:a
踢毽:b
c
N
a
+
-
b
c
总数
两部分的和
-重叠部分
=
=
韦恩图
约翰.维恩(John Venn1834—1923)
十九世纪英国著名的哲学家、数学家、逻辑学家,他在前几代人研究的基础上于1881年发明了维恩图。
维恩图用于展示不同的事物群组(集合)之间的数学或逻辑联系,尤其适合用来表示集合间的关系,它也常常被用来帮助推导关于集合运算的一些规律。
你
知
道
吗
?
重叠
走进生活
你看,穿花衣服的大雁多么漂亮啊!从前面数,它排在第6;从后面数,它排在第3。这一行大雁一共有多少只呢
20cm
20cm
5cm
重叠
走进生活
在生活中会发现一些重叠问题。
创造维恩图,梳理重叠问题的数量关系。
数
形
结
合
借助维恩图,建立了数学模型。
运用维恩图的模型,解决问题。
吸烟的爸爸
喝酒的爸爸
既吸烟又喝酒的爸爸
既不吸烟又不喝酒的爸爸又该怎么表示呢?
进一步探索更深奥的重叠问题。
……
在生活中会发现一些重叠问题。
创造维恩图,梳理重叠问题的数量关系。
数
形
结
合
借助维恩图,建立了数学模型。
运用维恩图的模型,解决问题。
吸烟的爸爸
喝酒的爸爸
既吸烟又喝酒的爸爸
既不吸烟又不喝酒的爸爸又该怎么表示呢?
下
课
了
