华东师大版数学九年级上册 22.3 实践与探索课件(共15张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 22.3 实践与探索课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 497.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
用一元二次方程解决简单的应用问题
1.列一元二次方程解决实际问题时,与应用一元一次方程一样,一般步骤为:(1)审题,找等量关系;(2)设________;(3)列_________;(4)解______;(5)检验并作答.
2.构建一元二次方程来解决实际问题时,必须验证方程的解是否符合____________。
3.几何图形问题常根据_________________公式列出一元二次方程.
4.若设每次的平均增长(或降低)率为x,原来的基数为a,则第一次增长(或降低)后的数量为____________,第二次增长(或降低)后的数量为_______________。
未知数
方程
方程
实际意义
面积(或体积)
a(1±x)
a(1±x)2
知识点1:用一元二次方程解决几何问题
1.一个面积为35 m2的矩形苗圃,它的长比宽多2 m,则这个苗圃的长为( )
A.5 m B.6 m C.7 m D.8 m
2.等腰梯形面积为160 cm2,上底比高多4 cm,下底比高多20 cm,这个梯形的高为( )
A.20 cm B.8 cm
C.8 cm或20 cm D.非以上答案
3.一个正方形的边长增加了3 cm,面积相应增加了39 cm2,则原来这个正方形的边长为____cm.
C
B
5
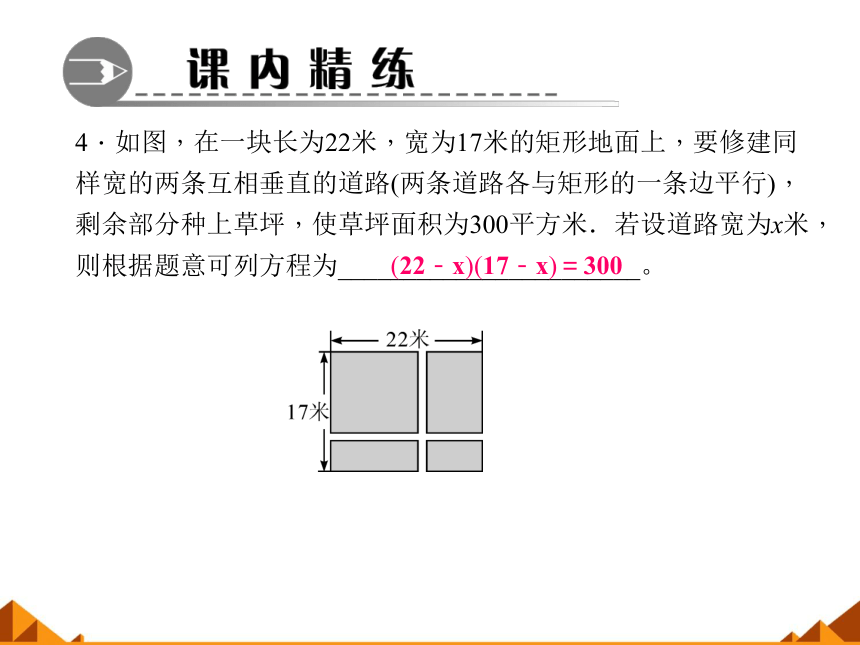
4.如图,在一块长为22米,宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列方程为_______________________。
(22-x)(17-x)=300
5.如图是一个矩形花园,花园的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图内阴影部分)种植的是不同花草.已知种植花草部分的面积为3600平方米,那么花园各角处的正方形观光休息亭的边长为多少米?
解:设正方形观光休息亭的边长为x米.依题意,有(100-2x)(50-2x)=3 600.整理,得x2-75x+350=0.解得x1=5,x2=70.∵x2=70>50,不合题意,舍去,∴x=5.答:矩形花园各角处的正方形观光休息亭的边长为5米
知识点2:用一元二次方程解决增长率问题
6.某药品经过两次降价,每瓶零售价由168元降为128元.已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得( )
A.168(1+x)2=128 B.168(1-x)2=128
C.168(1-2x)=128 D.168(1-x2)=128
B
7.某企业五月份的利润是25万元,预计七月份的利润将达到36万元.设平均月增长率为x,根据题意所列方程是___________________。
8.(2014·随州)某小区2013年绿化面积为2 000平方米,计划2015年绿化面积要达到2 880平方米.如果每年绿化面积的增长率相同,那么这个增长率是___________。
25(1+x)2=36
20%
知识点3:用一元二次方程解决其他问题
9.若两个连续整数的积是42,那么这两个整数的和是( )
A.13 B.-13
C.13或-13 D.12或-14
10.一个两位数等于它的个位数的平方,且个位数比十位数大3,则这个两位数是( )
A.25 B.36
C.25或36 D.-25或-36
C
C
11.一球以15 m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)近似满足关系式:h=15t-5t2,则小球在什么时刻的高度为10 m
解:由题意知,10=15t-5t2,解得t=1或t=2,所以小球在1秒或2秒时的高度为10 m
12.某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x2)=196
B.50+50(1+x2)=196
C.50+50(1+x)+50(1+x)2=196
D.50+50(1+x)+50(1+2x)=196
C
13.如图,在宽为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540 m2,求道路的宽.如果设小路宽为x m,根据题意,所列方程正确的是( )
A.(20-x)(32-x)=540
B.(20-x)(32-x)=100
C.(20+x)(32-x)=540
D.(20-x)(32+x)=540
A
14.有一间长20 m,宽15 m的会议室,在它的中间辅一块地毯,地毯子的面积是会议室面积的一半,四周未铺地毯的留空宽度相同,则留空宽度为________。
2.5m
15.(2014·丽水)如图,某小区规划在一个长30 m,宽20 m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,要使每一块花草的面积都为78 m2,那么通道的宽应设计成多少?设通道的宽为x m,由题意列方程________________________________。
(30-2x)(20-x)=6×78
16.某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率。
解:设3月份到5月份营业额的月平均增长率为x,根据题意,得400×(1+10%)(1+x)2=633.6,解得x=0.2=20%,x2=-2.2(不舍题意,舍去).答:3月份到5月份营业额的月平均增长率为20%
解:设我省每年产出的农作物秸秆总量为1,合理利用量的增长率是x,由题意,得1×30%·(1+x)2=1×60%,解得x1≈0.41,x2≈-2.41(不合题意,舍去).答:我省每年秸秆合理利用量的增长率约是41%
18.(2014·新疆)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
解:设AB的长度为x,则BC的长度为(100-4x)米.根据题意得(100-4x)x=400,解得x1=20,x2=5,则100-4x=20或100-4x=80.∵80>25,∴x2=5舍去,即AB=20,BC=20.答:羊圈的边长AB,BC分别是20米,20米
19.如图,要设计一幅宽20 cm,长30 cm的矩形图案,其中两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
用一元二次方程解决简单的应用问题
1.列一元二次方程解决实际问题时,与应用一元一次方程一样,一般步骤为:(1)审题,找等量关系;(2)设________;(3)列_________;(4)解______;(5)检验并作答.
2.构建一元二次方程来解决实际问题时,必须验证方程的解是否符合____________。
3.几何图形问题常根据_________________公式列出一元二次方程.
4.若设每次的平均增长(或降低)率为x,原来的基数为a,则第一次增长(或降低)后的数量为____________,第二次增长(或降低)后的数量为_______________。
未知数
方程
方程
实际意义
面积(或体积)
a(1±x)
a(1±x)2
知识点1:用一元二次方程解决几何问题
1.一个面积为35 m2的矩形苗圃,它的长比宽多2 m,则这个苗圃的长为( )
A.5 m B.6 m C.7 m D.8 m
2.等腰梯形面积为160 cm2,上底比高多4 cm,下底比高多20 cm,这个梯形的高为( )
A.20 cm B.8 cm
C.8 cm或20 cm D.非以上答案
3.一个正方形的边长增加了3 cm,面积相应增加了39 cm2,则原来这个正方形的边长为____cm.
C
B
5
4.如图,在一块长为22米,宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列方程为_______________________。
(22-x)(17-x)=300
5.如图是一个矩形花园,花园的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图内阴影部分)种植的是不同花草.已知种植花草部分的面积为3600平方米,那么花园各角处的正方形观光休息亭的边长为多少米?
解:设正方形观光休息亭的边长为x米.依题意,有(100-2x)(50-2x)=3 600.整理,得x2-75x+350=0.解得x1=5,x2=70.∵x2=70>50,不合题意,舍去,∴x=5.答:矩形花园各角处的正方形观光休息亭的边长为5米
知识点2:用一元二次方程解决增长率问题
6.某药品经过两次降价,每瓶零售价由168元降为128元.已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得( )
A.168(1+x)2=128 B.168(1-x)2=128
C.168(1-2x)=128 D.168(1-x2)=128
B
7.某企业五月份的利润是25万元,预计七月份的利润将达到36万元.设平均月增长率为x,根据题意所列方程是___________________。
8.(2014·随州)某小区2013年绿化面积为2 000平方米,计划2015年绿化面积要达到2 880平方米.如果每年绿化面积的增长率相同,那么这个增长率是___________。
25(1+x)2=36
20%
知识点3:用一元二次方程解决其他问题
9.若两个连续整数的积是42,那么这两个整数的和是( )
A.13 B.-13
C.13或-13 D.12或-14
10.一个两位数等于它的个位数的平方,且个位数比十位数大3,则这个两位数是( )
A.25 B.36
C.25或36 D.-25或-36
C
C
11.一球以15 m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)近似满足关系式:h=15t-5t2,则小球在什么时刻的高度为10 m
解:由题意知,10=15t-5t2,解得t=1或t=2,所以小球在1秒或2秒时的高度为10 m
12.某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x2)=196
B.50+50(1+x2)=196
C.50+50(1+x)+50(1+x)2=196
D.50+50(1+x)+50(1+2x)=196
C
13.如图,在宽为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540 m2,求道路的宽.如果设小路宽为x m,根据题意,所列方程正确的是( )
A.(20-x)(32-x)=540
B.(20-x)(32-x)=100
C.(20+x)(32-x)=540
D.(20-x)(32+x)=540
A
14.有一间长20 m,宽15 m的会议室,在它的中间辅一块地毯,地毯子的面积是会议室面积的一半,四周未铺地毯的留空宽度相同,则留空宽度为________。
2.5m
15.(2014·丽水)如图,某小区规划在一个长30 m,宽20 m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,要使每一块花草的面积都为78 m2,那么通道的宽应设计成多少?设通道的宽为x m,由题意列方程________________________________。
(30-2x)(20-x)=6×78
16.某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率。
解:设3月份到5月份营业额的月平均增长率为x,根据题意,得400×(1+10%)(1+x)2=633.6,解得x=0.2=20%,x2=-2.2(不舍题意,舍去).答:3月份到5月份营业额的月平均增长率为20%
解:设我省每年产出的农作物秸秆总量为1,合理利用量的增长率是x,由题意,得1×30%·(1+x)2=1×60%,解得x1≈0.41,x2≈-2.41(不合题意,舍去).答:我省每年秸秆合理利用量的增长率约是41%
18.(2014·新疆)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
解:设AB的长度为x,则BC的长度为(100-4x)米.根据题意得(100-4x)x=400,解得x1=20,x2=5,则100-4x=20或100-4x=80.∵80>25,∴x2=5舍去,即AB=20,BC=20.答:羊圈的边长AB,BC分别是20米,20米
19.如图,要设计一幅宽20 cm,长30 cm的矩形图案,其中两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
