华东师大版数学九年级上册 23.4 中位线课件(共15张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.4 中位线课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 908.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 12:05:49 | ||
图片预览




文档简介
(共15张PPT)
23.4 中位线
问 题
如图,A、B两点被池塘隔开,现要测出A、B两点的距离,但无法测量怎么办 这时,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,然后测量出DE的长度,就能知道AB的距离了。这是什么道理呢?
A
E
D
C
B
探究发现
A
B
C
D
E
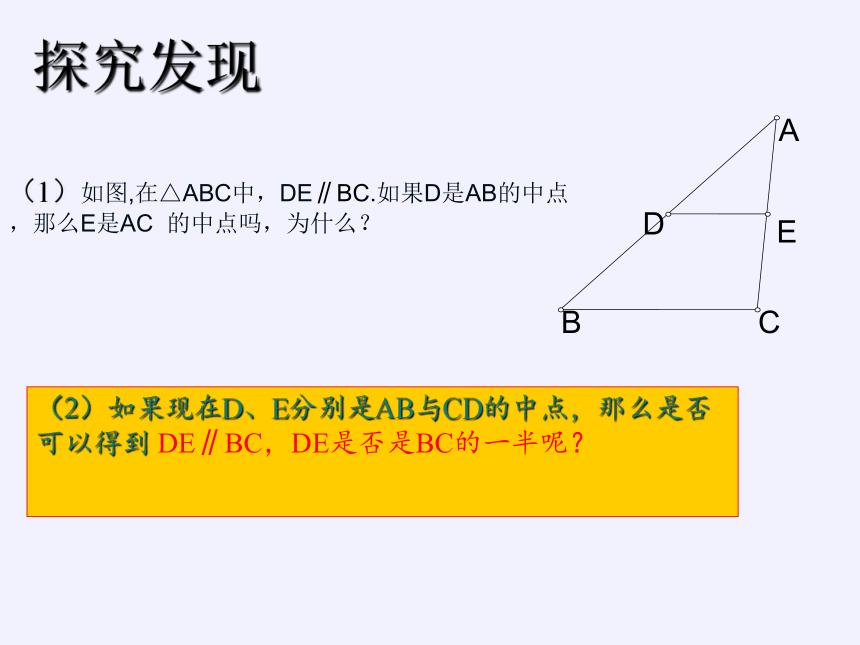
(1)如图,在△ABC中,DE∥BC.如果D是AB的中点,那么E是AC 的中点吗,为什么?
(2)如果现在D、E分别是AB与CD的中点,那么是否可以得到 DE∥BC,DE是否是BC的一半呢?
合作探究
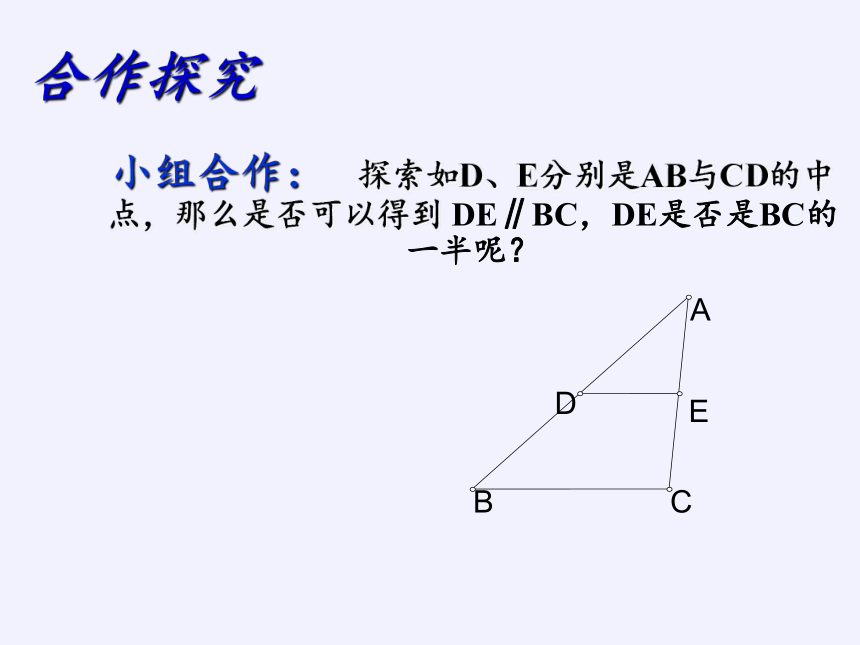
小组合作: 探索如D、E分别是AB与CD的中点,那么是否可以得到 DE∥BC,DE是否是BC的一半呢?
A
B
C
D
E
C
B
A
F
E
D
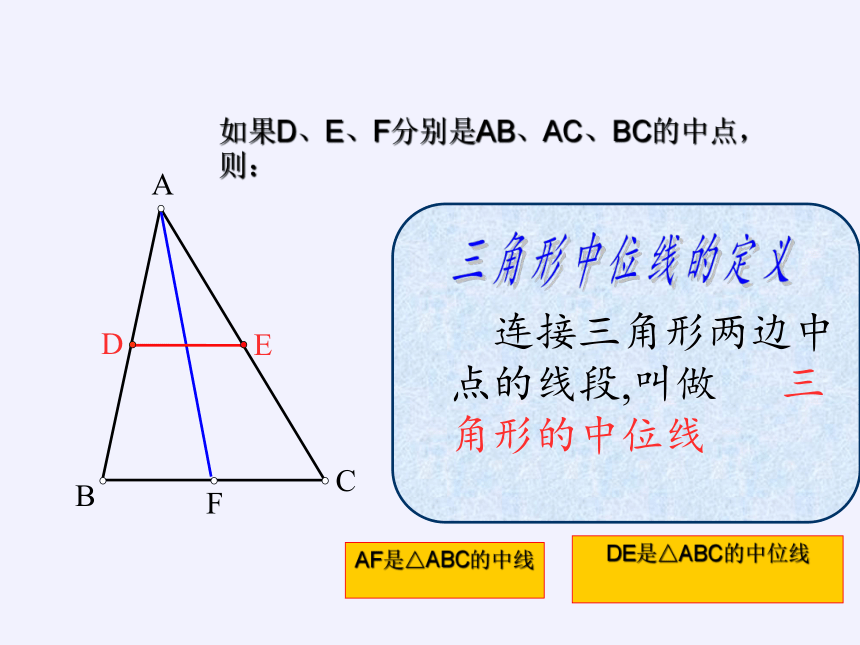
连接三角形两边中点的线段,叫做 三角形的中位线
三角形中位线的定义
AF是△ABC的中线
如果D、E、F分别是AB、AC、BC的中点,则:
DE是△ABC的中位线
求证:
A
B
C
D
E
已知: 中,点D、E分别是AB、AC的中点。
证明:
∵点D、E分别是AB、AC的中点。
∴
∵∠A=∠A
∴△ADE∽△ABC
∴∠ADE=∠B,
∴
A
B
C
D
E
三角形中位线性质定理:
三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的数学语言表示为:
∵△ABC中,点D、E分别是AB、 AC的中点
∴ DE是△ABC的中位线
或 ∵△ABC中,AD=DB,AE=EC
∴ DE是△ABC的中位线
∴
① 证明线段的平行问题(位置关系)
② 证明一条线段是另一条线段的2倍或1/2 (数量关系)
用 途
友情提醒:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
理解三角形的中位线定义的两层含义:
同学们,中位线的知识掌握了吗?我们一起去检验一下吧!
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=10cm,
则DE= cm,为什么?
(3) S△ADE:S△ABC= .
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
算一算
1:4
求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图,在△ABC中,D、E、F分别是AB、BC、AC的中点.
求证: AE与DF互相平分.
证明:连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行 于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE与DF互相平分(平行四边形的对角线互相平分).
证一证
例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证:
证明 :连结ED,
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC,
(三角形的中位线平行于第三边并且等于第三边的一半),
∴ △ACG∽△DEG,
∴
∴
概括
三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的
F
布置作业
课本79-80页2、3、4
谢 谢
23.4 中位线
问 题
如图,A、B两点被池塘隔开,现要测出A、B两点的距离,但无法测量怎么办 这时,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,然后测量出DE的长度,就能知道AB的距离了。这是什么道理呢?
A
E
D
C
B
探究发现
A
B
C
D
E
(1)如图,在△ABC中,DE∥BC.如果D是AB的中点,那么E是AC 的中点吗,为什么?
(2)如果现在D、E分别是AB与CD的中点,那么是否可以得到 DE∥BC,DE是否是BC的一半呢?
合作探究
小组合作: 探索如D、E分别是AB与CD的中点,那么是否可以得到 DE∥BC,DE是否是BC的一半呢?
A
B
C
D
E
C
B
A
F
E
D
连接三角形两边中点的线段,叫做 三角形的中位线
三角形中位线的定义
AF是△ABC的中线
如果D、E、F分别是AB、AC、BC的中点,则:
DE是△ABC的中位线
求证:
A
B
C
D
E
已知: 中,点D、E分别是AB、AC的中点。
证明:
∵点D、E分别是AB、AC的中点。
∴
∵∠A=∠A
∴△ADE∽△ABC
∴∠ADE=∠B,
∴
A
B
C
D
E
三角形中位线性质定理:
三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的数学语言表示为:
∵△ABC中,点D、E分别是AB、 AC的中点
∴ DE是△ABC的中位线
或 ∵△ABC中,AD=DB,AE=EC
∴ DE是△ABC的中位线
∴
① 证明线段的平行问题(位置关系)
② 证明一条线段是另一条线段的2倍或1/2 (数量关系)
用 途
友情提醒:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
理解三角形的中位线定义的两层含义:
同学们,中位线的知识掌握了吗?我们一起去检验一下吧!
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=10cm,
则DE= cm,为什么?
(3) S△ADE:S△ABC= .
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
算一算
1:4
求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图,在△ABC中,D、E、F分别是AB、BC、AC的中点.
求证: AE与DF互相平分.
证明:连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行 于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE与DF互相平分(平行四边形的对角线互相平分).
证一证
例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证:
证明 :连结ED,
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC,
(三角形的中位线平行于第三边并且等于第三边的一半),
∴ △ACG∽△DEG,
∴
∴
概括
三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的
F
布置作业
课本79-80页2、3、4
谢 谢
