华东师大版数学九年级上册 23.5 位似图形课件(共15张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.5 位似图形课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 12:09:03 | ||
图片预览





文档简介
(共15张PPT)
23.5 位似图形
一、学一学——展示你的身手
⒈如果两个多边形不仅_____________,而且__________________________,那么这样的两个图形叫做位似图形;这个点叫做____________ 。
⒉两个位似图形的位似比也就是指他们的______________比。
若两个图形相似,且每组对应顶点所在的直线都经过同一个点。则这样的两个图形称做位似图形,该点称为位似中心,相似比称作位似比。
概念剖析
1.判断:
⑴两个相似图形一定是位似图形( )
⑵两个位似图形一定是相似图形( )
⑶已知△ABC和△A1B1C1,如果顶点所在直线AA1,BB1,CC1
相交于同一点O,那么△ABC与△A1B1C1是位似图形( )
2.如图,D、E分别是AB、AC上的点,
⑴如果DE∥BC,那么△ADE和△ABC是位似图形吗?
为什么?
⑵如果△ADE和△ABC是位似图形,
那么DE∥BC吗
为什么?
(一)(做一做)
二、试一试——相信你的能力
A
E
B
C
D
(1)
(2)
(3)
(4)
(5)
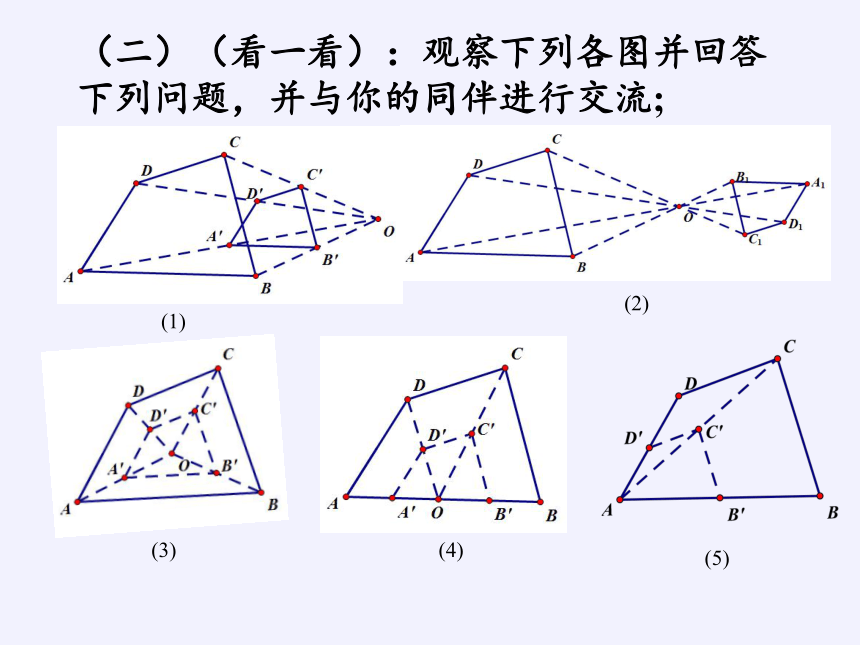
(二)(看一看):观察下列各图并回答下列问题,并与你的同伴进行交流;
在图中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系
位似图形上任意一对对应点到位似中心的距离之比等于位似比(——位似图形的性质)
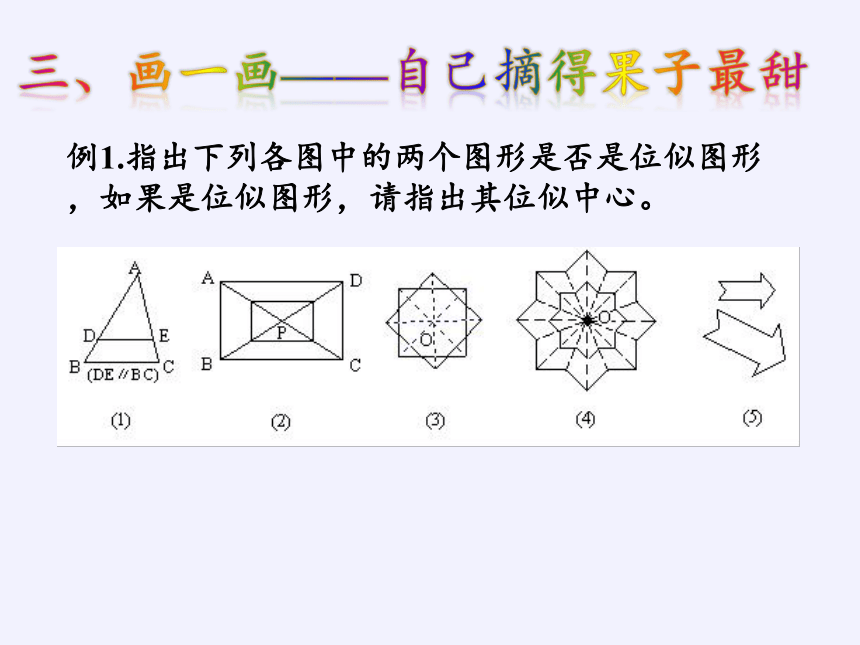
三、画一画——自己摘得果子最甜
例1.指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心。
(1)将△ABC按比例缩小为原来的1/2:
还有其他方法吗
利用位似把图形放大或缩小
(3)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢
D
E
F
A
O
B
C
还有其他方法吗
结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1.
(2)如何把三角形ABC放大为原来的2倍
位似图形:
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比
位似图形应用:放大或缩小原图形;
小结 拓展
正向或反向
截取或延长
两个位似图形中的对应角____,对应线
段_____,对应顶点的连线必经过_______。
2.位似图形上某一对对应点到位似中心的
距离分别为5和10,则它们的位似比为___。
3.四边形ABCD和四边形A’B’C’D’位似,O为位
似中心,若OA:OA’=1:4,那么
S四边形ABCD:S四边形A’B’C’D’=_____。
随堂小练(一)
面向全体,巩固双基
在一次成像实验中,已知所成像的大小是
原实物的一半,则像与实物的位置有几种情况?
分析不同位置的像之间的联系?
两种
关于位似中心成中心对称
随堂小练(二)
同侧正立,异侧倒立
学科整合,能力提升
学科衔接
餐后甜点
谢 谢
23.5 位似图形
一、学一学——展示你的身手
⒈如果两个多边形不仅_____________,而且__________________________,那么这样的两个图形叫做位似图形;这个点叫做____________ 。
⒉两个位似图形的位似比也就是指他们的______________比。
若两个图形相似,且每组对应顶点所在的直线都经过同一个点。则这样的两个图形称做位似图形,该点称为位似中心,相似比称作位似比。
概念剖析
1.判断:
⑴两个相似图形一定是位似图形( )
⑵两个位似图形一定是相似图形( )
⑶已知△ABC和△A1B1C1,如果顶点所在直线AA1,BB1,CC1
相交于同一点O,那么△ABC与△A1B1C1是位似图形( )
2.如图,D、E分别是AB、AC上的点,
⑴如果DE∥BC,那么△ADE和△ABC是位似图形吗?
为什么?
⑵如果△ADE和△ABC是位似图形,
那么DE∥BC吗
为什么?
(一)(做一做)
二、试一试——相信你的能力
A
E
B
C
D
(1)
(2)
(3)
(4)
(5)
(二)(看一看):观察下列各图并回答下列问题,并与你的同伴进行交流;
在图中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系
位似图形上任意一对对应点到位似中心的距离之比等于位似比(——位似图形的性质)
三、画一画——自己摘得果子最甜
例1.指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心。
(1)将△ABC按比例缩小为原来的1/2:
还有其他方法吗
利用位似把图形放大或缩小
(3)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢
D
E
F
A
O
B
C
还有其他方法吗
结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1.
(2)如何把三角形ABC放大为原来的2倍
位似图形:
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比
位似图形应用:放大或缩小原图形;
小结 拓展
正向或反向
截取或延长
两个位似图形中的对应角____,对应线
段_____,对应顶点的连线必经过_______。
2.位似图形上某一对对应点到位似中心的
距离分别为5和10,则它们的位似比为___。
3.四边形ABCD和四边形A’B’C’D’位似,O为位
似中心,若OA:OA’=1:4,那么
S四边形ABCD:S四边形A’B’C’D’=_____。
随堂小练(一)
面向全体,巩固双基
在一次成像实验中,已知所成像的大小是
原实物的一半,则像与实物的位置有几种情况?
分析不同位置的像之间的联系?
两种
关于位似中心成中心对称
随堂小练(二)
同侧正立,异侧倒立
学科整合,能力提升
学科衔接
餐后甜点
谢 谢
