北师大版四年级下册2.3《探索与发现:三角形内角和》导学精练
文档属性
| 名称 | 北师大版四年级下册2.3《探索与发现:三角形内角和》导学精练 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 08:44:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版四年级下册2.3《探索与发现:三角形内角和》导学精练
1.三角形的内角和是多少度
分析与解答:
(1)拿出你剪下来的三角形,把 3 个角剪下来,再把这 3 个角拼在一起,你发现了什么
我们把 3 个角拼在一起,发现这 3 个角组成了一个( )角,所以,这个三角形的内角和是( )。
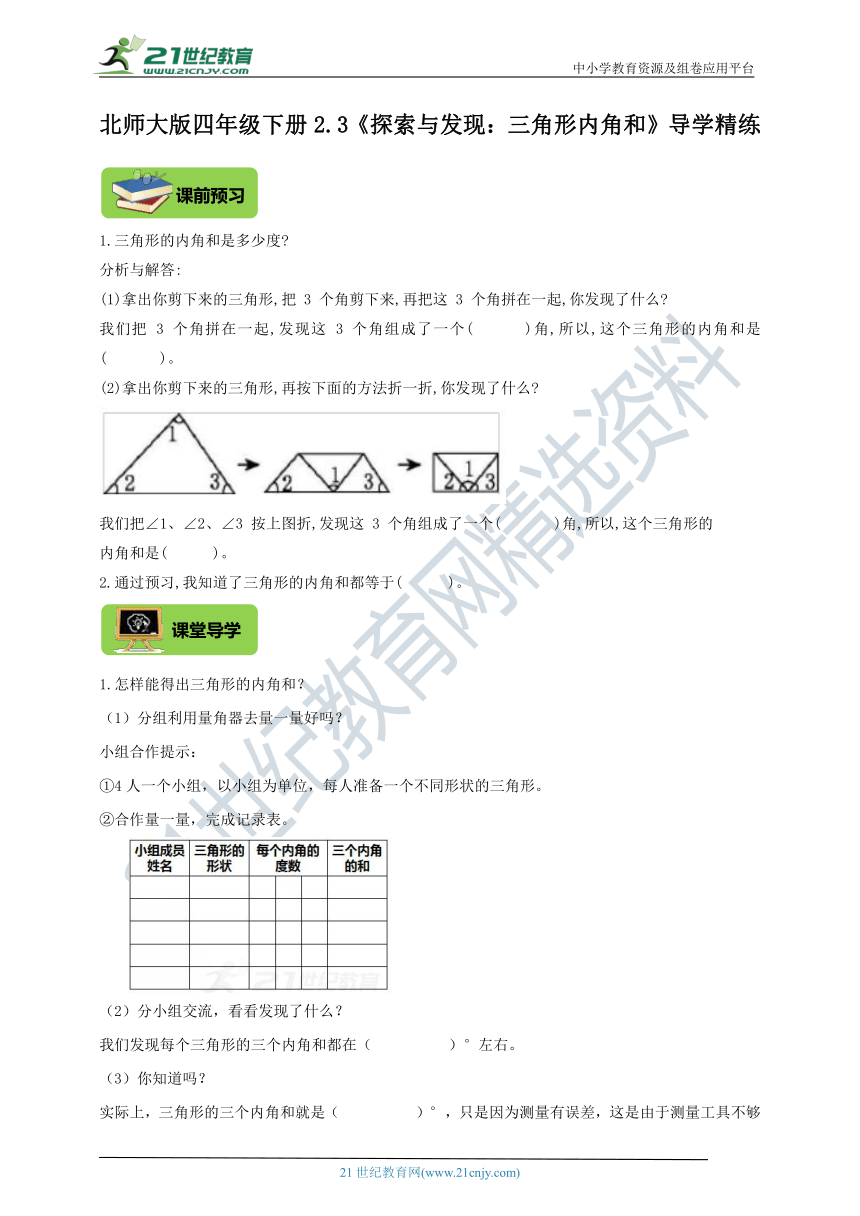
(2)拿出你剪下来的三角形,再按下面的方法折一折,你发现了什么
我们把∠1、∠2、∠3 按上图折,发现这 3 个角组成了一个( )角,所以,这个三角形的
内角和是( )。
2.通过预习,我知道了三角形的内角和都等于( )。
1.怎样能得出三角形的内角和?
(1)分组利用量角器去量一量好吗?
小组合作提示:
①4人一个小组,以小组为单位,每人准备一个不同形状的三角形。
②合作量一量,完成记录表。
(2)分小组交流,看看发现了什么?
我们发现每个三角形的三个内角和都在( )°左右。
(3)你知道吗?
实际上,三角形的三个内角和就是( )°,只是因为测量有误差,这是由于测量工具不够标准或测量时不够细致造成的。
2.有什么验证你的想法?说一说,做一做。
方法一:180°是一个( )角,我们把三角形的三个角撕下来,拼在一起;
方法二:用折叠的方法
3.我的结论是:_____________________________________
4. 你知道?
5.“试一试”
(1)猜一猜,可能是什么三角形?
①提示:三角形的内角和是( )度,可以先算出( )的角。
②算一算,说一说。
( )°-( )°-( )°=( )°
三个角都是( )角,所以它是( )三角形。
(2)你还能猜出是什么三角形吗?
①剩下两个角的度数和应该是:____________________
②如果一个角是( )°,另一个角是( )°,那么这是一个( )三角形。
如果一个角是( )°,另一个角是( )°,那么这是一个( )三角形。
③我知道等边三角形的每个角是( )°,遮住的是等边三角形吗?
(4)你发现了什么?
知道三角形中的( 个角的度数,可以准确的判断这个三角形的类型,如果只知道三角形中任意( 个角的度数,会有各种猜测。
1、填空。
1. 三角形的内角和是( )°。
2.在一个三角形中,有两个角分别是36°和75°,则该三角形的第三个角是( ) 度,这个三角形是( )三角形。
3.在一个三角形中,有两个角都是45°,这个三角形既是( )三角形,又是( )三角形。
4.求出下面角的度数。
∠A=( ) ∠C=( ) ∠B=( )
5.直角三角形的两个锐角和是( )度。
6.把一个长方形分割成两个三角形,每一个小三角形的内角和是( )度。
二、在能组成三角形的三个角后面的横线里打“√“,不能组成三角形的打“×。
(1)40° 45° 70° ( )
(2)60° 60° 60° ( )
(3)80° 20° 80° ( )
(4)90° 43° 57° ( )
三、画一画,试一试,求出各多边形的内角和。
、
参考答案
课前预习
1. (1)平 180° (2)平 180°
2. 180°
课堂小练笔
一、1.【解析】直接根据三角形的内角和是180°求解。
【答案】180。
2.【解析】根据三角形的内角和定理,求出第三个角,再判断三角形的形状,即第三个角是180°-36°-75°=69°,则这个三角形是锐角三角形。
【答案】69°;锐角。
3.【解析】根据三角形内角和是180°算出剩下的这个角是90°,有一个角是直角的等腰三角形是等腰直角三角形,进而得出结论。
【答案】直角;等腰。
4.【解析】根据三角形内角和是180°,连续减去已知两个角的度数即可求解。
【答案】55°;113°;55°。
5.【解析】根据三角形内角和是180°减去直角的度数即可求出两个锐角和。
【答案】90。
6.【解析】不论三角形的形状大小,内角和都是180度。
【答案】180。
二、【解析】计算一下三个角的度数之和,如果等于180度就能组成三角形,否则不能。
【答案】(1)×,(2)√,(3)√,(4)×。
三、【解析】先从多边形的一个顶点开始把它分成三角形,然后数数一共是几个三角形,是几个,就用几乘180就是该多边形的内角和,据此解答即可。
【答案】
180°×3=540°
180°×4=720°
180°×5=900°
课前预习
课堂导学
课堂小练笔uxiao’li’a’b
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版四年级下册2.3《探索与发现:三角形内角和》导学精练
1.三角形的内角和是多少度
分析与解答:
(1)拿出你剪下来的三角形,把 3 个角剪下来,再把这 3 个角拼在一起,你发现了什么
我们把 3 个角拼在一起,发现这 3 个角组成了一个( )角,所以,这个三角形的内角和是( )。
(2)拿出你剪下来的三角形,再按下面的方法折一折,你发现了什么
我们把∠1、∠2、∠3 按上图折,发现这 3 个角组成了一个( )角,所以,这个三角形的
内角和是( )。
2.通过预习,我知道了三角形的内角和都等于( )。
1.怎样能得出三角形的内角和?
(1)分组利用量角器去量一量好吗?
小组合作提示:
①4人一个小组,以小组为单位,每人准备一个不同形状的三角形。
②合作量一量,完成记录表。
(2)分小组交流,看看发现了什么?
我们发现每个三角形的三个内角和都在( )°左右。
(3)你知道吗?
实际上,三角形的三个内角和就是( )°,只是因为测量有误差,这是由于测量工具不够标准或测量时不够细致造成的。
2.有什么验证你的想法?说一说,做一做。
方法一:180°是一个( )角,我们把三角形的三个角撕下来,拼在一起;
方法二:用折叠的方法
3.我的结论是:_____________________________________
4. 你知道?
5.“试一试”
(1)猜一猜,可能是什么三角形?
①提示:三角形的内角和是( )度,可以先算出( )的角。
②算一算,说一说。
( )°-( )°-( )°=( )°
三个角都是( )角,所以它是( )三角形。
(2)你还能猜出是什么三角形吗?
①剩下两个角的度数和应该是:____________________
②如果一个角是( )°,另一个角是( )°,那么这是一个( )三角形。
如果一个角是( )°,另一个角是( )°,那么这是一个( )三角形。
③我知道等边三角形的每个角是( )°,遮住的是等边三角形吗?
(4)你发现了什么?
知道三角形中的( 个角的度数,可以准确的判断这个三角形的类型,如果只知道三角形中任意( 个角的度数,会有各种猜测。
1、填空。
1. 三角形的内角和是( )°。
2.在一个三角形中,有两个角分别是36°和75°,则该三角形的第三个角是( ) 度,这个三角形是( )三角形。
3.在一个三角形中,有两个角都是45°,这个三角形既是( )三角形,又是( )三角形。
4.求出下面角的度数。
∠A=( ) ∠C=( ) ∠B=( )
5.直角三角形的两个锐角和是( )度。
6.把一个长方形分割成两个三角形,每一个小三角形的内角和是( )度。
二、在能组成三角形的三个角后面的横线里打“√“,不能组成三角形的打“×。
(1)40° 45° 70° ( )
(2)60° 60° 60° ( )
(3)80° 20° 80° ( )
(4)90° 43° 57° ( )
三、画一画,试一试,求出各多边形的内角和。
、
参考答案
课前预习
1. (1)平 180° (2)平 180°
2. 180°
课堂小练笔
一、1.【解析】直接根据三角形的内角和是180°求解。
【答案】180。
2.【解析】根据三角形的内角和定理,求出第三个角,再判断三角形的形状,即第三个角是180°-36°-75°=69°,则这个三角形是锐角三角形。
【答案】69°;锐角。
3.【解析】根据三角形内角和是180°算出剩下的这个角是90°,有一个角是直角的等腰三角形是等腰直角三角形,进而得出结论。
【答案】直角;等腰。
4.【解析】根据三角形内角和是180°,连续减去已知两个角的度数即可求解。
【答案】55°;113°;55°。
5.【解析】根据三角形内角和是180°减去直角的度数即可求出两个锐角和。
【答案】90。
6.【解析】不论三角形的形状大小,内角和都是180度。
【答案】180。
二、【解析】计算一下三个角的度数之和,如果等于180度就能组成三角形,否则不能。
【答案】(1)×,(2)√,(3)√,(4)×。
三、【解析】先从多边形的一个顶点开始把它分成三角形,然后数数一共是几个三角形,是几个,就用几乘180就是该多边形的内角和,据此解答即可。
【答案】
180°×3=540°
180°×4=720°
180°×5=900°
课前预习
课堂导学
课堂小练笔uxiao’li’a’b
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
