2021年人教版八年级数学上册15.1.2 分式的基本性质教学课件(35张)
文档属性
| 名称 | 2021年人教版八年级数学上册15.1.2 分式的基本性质教学课件(35张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 20:56:37 | ||
图片预览











文档简介
(共35张PPT)
第十五章 分式
15.1.2 分式的基本性质
人教版 数学 八年级 上册
学习目标
理解并掌握分式的基本性质.(重点)
会运用分式的基本性质进行分式的约分和通分.(难点)
4 相等吗
分数的 基本性质
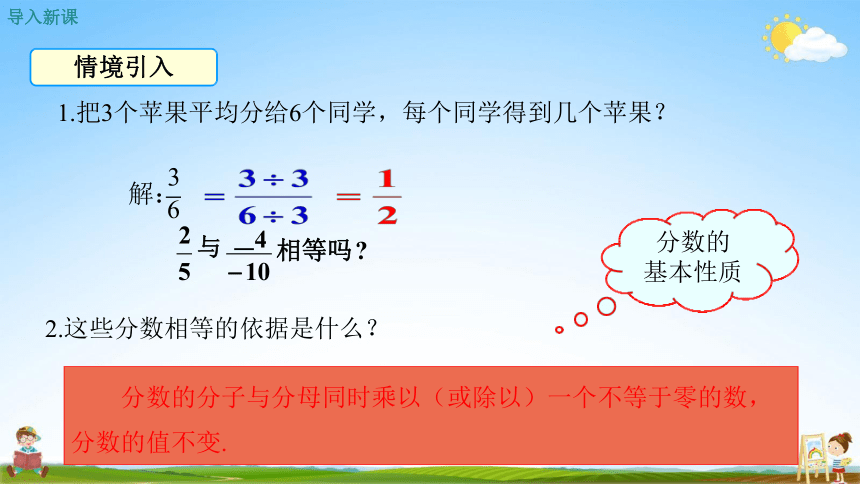
分数的分子与分母同时乘以(或除以)一个不等于零的数, 分数的值不变.
2.这些分数相等的依据是什么?
导入新课
情境引入
1.把3个苹果平均分给6个同学,每个同学得到几个苹果?
3
6
2 与
5 10
解:
讲授新课
分式的基本性质
一
思考:下列两式成立吗?为什么?
(c 0)
(c 0)
3 3c
4 4c
5c 5
6c 6
分数的基本性质:
a
即对于任意一个分数 有: b
(c 0)
a a c b b c
a a c b b c
mn
n
m
n
2
”相等吗?
”与“
a ”与“ 1 ”;分式
2 a 2
你认为分式“
a,m,n 均不为 0)
想一想:类比分数的基本性质,你能猜想分式有什么性质 吗?
思考:
分式的基本性质:
分式的分子与分母乘以(或除以)同一个不等于0的整式, 分式的值不变.
上述性质可以用式表示为:
(C 0).
A A C , A A C B B C B B C
其中A,B,C是整式.
知识要点
x3
xy
y
6 x 2
,
3 x 2 3 xy x y
1)
( x 0)
(x 2 )
( 2 x)
a
ab
a 2b
a 2
a 2b
1 (
) 2a b (
2ab b2 )
2)
,
( b 0).
例1
典例精析
想一想:(1)
填空: 看分母如何变化,想分子如何变中化为.什么不给
出x ≠0,而(2) 看分子如何变化,想分母如何变中化却.给出了b ≠0
想一想: 运用分式的基本性质应注意什么
(1)“都”
(2) “同一个”
(3) “不为0”
例2 不改变分式的值,把下列各式的分子与分母的各项系数都化 为整数.
⑴ ⑵
(0.01x 5) 100 x 500 (0.3x 0.04) 100 30x 4
解:
5
(0.6a 5 b) 30
3 18a 50b
21a 12b
(0.7a 2 b) 30
⑴
⑵
⑶
7b
3a 10m
解:(1)原式=
2x
5 y
3n
3a
(2)原式= 7b
(3)原式= 10m
3n
练一练
不改变分式的值,使下列分子与分母都不含“-”号
2 x 5 y
分式的约分
二
xy x y
x2
x2
2x x 2
x2
x
x x
x 2
( x 2 xy ) x x y
x x 1
( x 2 2 x ) x x 2
( )
( )
想一想:
联想分数的约分,由例1你能想出如何对分式进行约分?
与分数约分类似,关键是要找出分式的分子与分母的最简公分母.
像这样,根据分式的基本性质,把一个分式的分子与分母的 公因式约去,叫做分式的约分.
知识要点
约分的定义
分子与分母没有公因式的式子,叫做最简分式.
分式的约分,一般要约去分子和分母所有的公因式,使所得 的结果成为最简分式或整式.
经过约分后的分式x
y,其分子与分母没有公因.像这样
2 x
5 x y
5 x
2 0 x 2 y
2 0 x 2
1
5 xy
5 xy
20 x 2 y 4 x 5 xy 4 x
你对他们俩的解法有何看法?说说看!
一般约分要彻底, 使分子、分母没有公因式.
议一议
5 x y
2 0 x 2 y
2 5 a 2 b c 3
典例精析
例3 约分: 1)
1 5 a b 2 c
分析:为约分要先找出分子和分母的公因式. 找公因式方法:
约去系数的最大公约数.
约去分子分母相同因式的最低次幂.
解:
5ac2
3b
1)
25a2bc3 5abc 5ac2
15ab2c 5abc 3b
(公因式是5ac2)
2
x2
2)
9
x 6x 9
x 2
x 2
解: 2)
.
9
x 3
6 x 9
( x 3)( x 3) x 3
( x 3)2
分析:约分时,分子或分母若是多项式,能分解则必须先进行因 式分解.再找出分子和分母的公因式进行约分.
知识要点
约分的基本步骤
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去 相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去 分子﹑分母所有的公因式.
注意事项:
约分前后分式的值要相等.
约分的关键是确定分式的分子和分母的公因式.
约分是对分子、分母的整体进行的,也就是分子的整体和分母的 整体都除以同一个因式.
分式的通分
三
通分:
问题1:
7
1
8
与
1 2
最小公倍数:24
12
解: 7
24
14
12 2
7 2
1
1 3
8 8 3 24
3
分数的通分:把几个异分母的分数化成同分母的分数,而不改变分 数的值,叫做分数的通分.
通分的关键是确定几 个分母的最小公倍数
想一想:
联想分数的通分,由例1你能想出如何对分式进行通分?
a b
a 2 b
=
2
)
2 a - b
a a
2 b
=
(b≠0)
a + b ( a2 + ab )
( 2a b - b2
问题2:填空
知识要点
分式的通分的定义
与分数的通分类似,根据分式的基本性质,使分子、分母同乘适当的 整式(即最简公分母),把分母不相同的分式变成分母相同的分式,
这种变形叫分式的通分.如分式
b
. a b
分后分母都变成了a2b a +
与 分母分别是ab,a2,通
2 a - b
a 2
最简公分母
为通分先要确定各分式的公分母,一般取各分母的所有因式的最高 次幂的积作公分母,叫做最简公分母.
注意:确定最简公母是通分的关键.
3
a b 2 c
a b
(1 ) 与
2 a 2 b
b2
2 a2 c
例4 通分:
,
3bc
3 3 ·bc
= =
2a2b 2a2b ·bc 2a2b2c
2
2
2 2
.
2a b c
a - b (a - b) ·2a 2a2 - 2ab
=
=
ab c ab c ·2a
解:(1)最简公分母是2a2b2c
(2)最简公分母是(x+5)(x-5)
2 x 2 x( x + 5)
2 x2 + 5x
= =
x - 5 ( x - 5)( x + 5)
,
x2 - 25
3x2 - 5x
3x = 3x(x - 5) =
x + 5 (x + 5)(x - 5)
.
x2 - 25
( 2 )
3 x
x 5 x 5
2 x
与
最 简 公 分 母
1·(x-5)
1·(x+5)
1 (x-5) (x+5)
不同的因式
b
a
xy
x 2
y 2
x 2
与
例5 通分:
方法归纳:先将分母因式分解,再将每一个因式看成一个 整体,最后确定最简公分母.
(x+y)(x-y)
解:最简公分母是x(x+y)(x-y)
x(x+y)
,
a a
ax
ax
= =
=
( x - y)( x + y)
x( x - y)( x + y)
x3 - xy 2
x2 - y 2 b
b
b( x - y) bx - by ,
=
= =
x( x + y) x( x - y)( x + y)
x2 + xy x3 - xy 2
确定几个分式的最简公分母的方法:
因式分解
系数:各分式分母系数的最小公倍数;
字母:各分母的所有字母的最高次幂
多项式:各分母所有多项式因式的最高次幂
积
方法归纳
想一想:
分数和分式在约分和通分的做法上有什么共同点?这 些做法的根据是什么?
约分 通分
分数 找分子与分母的 最大公约数 找所有分母的 最小公倍数
分式 找分子与分母的公 因式 找所有分母的 最简公分母
依据 分数或分式的基本性质
当堂练习
D .
x 2
x 2
x 2
a b y 2
4
x y
A . B .
b a
x y
C .
x 2
y 2
2.下列各式中是最简分式的( B )
A.
c c
b a a b
B.
c
c
C.
c c b a a b
D.
a b a b
c
c
b a a b
1.下列各式成立的是( D )
B.不变 D.缩小四倍
y
3.若把分式 x
y 的 x 和y 都扩大两倍,则分式
的值( B ) A.扩大两倍 C.缩小两倍
x y
y中的X和Y都扩大3倍,那么分式
4.若把分式 x
的值( ).
A.扩大3倍 C.扩大4倍
B.扩大9倍 D.不变
解:
ac
a
)
x y
x y
2 ( x
y) y
)
2 bc
x 2
m 2
y 2
1)
ac
; ( 2)
; ( 3 )
x 2
( x y) y
xy 2
1 2bc 2b
m
xy
2 xy
; ( 4 ) m 2 1
5.约分
x y 2
x 2
x
x 2
y 2
3)
x y
x y
(x x y)
( x y)2
m 2
m
4)
.
2 x y
m
m( m 1)
m 1
m 2 1
(1 m )(1 m )
1
3
,
3 a b 3 4 a 2 b
1)
6.通分:
解:最简公分母是12a2b3
1 4 a
=
2
3 a b 3
3
1 2 a 2 b 3
9 b 2
4 a b
1 2 a 2 b 3
=
解:最简公分母是(2x+1)(2x-1)
4 4 ( 2 x + 1 )
8 x + 4
- ( 2 x - 1 ) ( 2 x + 1 )
- 4 x 2 + 1
= =
4
1 2 x
( 2 ) ,
4 x 2 1
2 x
1 - 2 x
2 x
4 x 2 -1
小贴士:在分式的约分与通分中,通常碰到如下因式符号变形:
(b-a)2=(a-b)2;b-a=-(a-b).
( 3 )
x
x 2
2 x y
( x y ) 2
y 2
,
解:最简公分母是(x+y)2(x-y)
2 2
2
2 x y 2
2 x y 2 x y ( x - y )
2 x 2 y -
=
=
( x + y ) ( x + y ) ( x -
y ) ( x + y )
( x - y )
2
2
2
2
y 2
x x ( x + y )
x 2 +
=
=
x - y
( x + y ) ( x -
y ) ( x + y ) ( x - y )
课堂小结
分 式 的 基 本 性 质
内
容
作
用
分式进行约分 和通分的依据
B B C B B C
A A C , A A C
(C 0).
注
意
分子分母同时进行;
分子分母只能同乘或同除,不能进 行同加或同减;
分子分母只能同乘或同除同一个整 式;
除式是不等于零的整式
进行分式运算的基 础
谢谢观看
Thank You
第十五章 分式
15.1.2 分式的基本性质
人教版 数学 八年级 上册
学习目标
理解并掌握分式的基本性质.(重点)
会运用分式的基本性质进行分式的约分和通分.(难点)
4 相等吗
分数的 基本性质
分数的分子与分母同时乘以(或除以)一个不等于零的数, 分数的值不变.
2.这些分数相等的依据是什么?
导入新课
情境引入
1.把3个苹果平均分给6个同学,每个同学得到几个苹果?
3
6
2 与
5 10
解:
讲授新课
分式的基本性质
一
思考:下列两式成立吗?为什么?
(c 0)
(c 0)
3 3c
4 4c
5c 5
6c 6
分数的基本性质:
a
即对于任意一个分数 有: b
(c 0)
a a c b b c
a a c b b c
mn
n
m
n
2
”相等吗?
”与“
a ”与“ 1 ”;分式
2 a 2
你认为分式“
a,m,n 均不为 0)
想一想:类比分数的基本性质,你能猜想分式有什么性质 吗?
思考:
分式的基本性质:
分式的分子与分母乘以(或除以)同一个不等于0的整式, 分式的值不变.
上述性质可以用式表示为:
(C 0).
A A C , A A C B B C B B C
其中A,B,C是整式.
知识要点
x3
xy
y
6 x 2
,
3 x 2 3 xy x y
1)
( x 0)
(x 2 )
( 2 x)
a
ab
a 2b
a 2
a 2b
1 (
) 2a b (
2ab b2 )
2)
,
( b 0).
例1
典例精析
想一想:(1)
填空: 看分母如何变化,想分子如何变中化为.什么不给
出x ≠0,而(2) 看分子如何变化,想分母如何变中化却.给出了b ≠0
想一想: 运用分式的基本性质应注意什么
(1)“都”
(2) “同一个”
(3) “不为0”
例2 不改变分式的值,把下列各式的分子与分母的各项系数都化 为整数.
⑴ ⑵
(0.01x 5) 100 x 500 (0.3x 0.04) 100 30x 4
解:
5
(0.6a 5 b) 30
3 18a 50b
21a 12b
(0.7a 2 b) 30
⑴
⑵
⑶
7b
3a 10m
解:(1)原式=
2x
5 y
3n
3a
(2)原式= 7b
(3)原式= 10m
3n
练一练
不改变分式的值,使下列分子与分母都不含“-”号
2 x 5 y
分式的约分
二
xy x y
x2
x2
2x x 2
x2
x
x x
x 2
( x 2 xy ) x x y
x x 1
( x 2 2 x ) x x 2
( )
( )
想一想:
联想分数的约分,由例1你能想出如何对分式进行约分?
与分数约分类似,关键是要找出分式的分子与分母的最简公分母.
像这样,根据分式的基本性质,把一个分式的分子与分母的 公因式约去,叫做分式的约分.
知识要点
约分的定义
分子与分母没有公因式的式子,叫做最简分式.
分式的约分,一般要约去分子和分母所有的公因式,使所得 的结果成为最简分式或整式.
经过约分后的分式x
y,其分子与分母没有公因.像这样
2 x
5 x y
5 x
2 0 x 2 y
2 0 x 2
1
5 xy
5 xy
20 x 2 y 4 x 5 xy 4 x
你对他们俩的解法有何看法?说说看!
一般约分要彻底, 使分子、分母没有公因式.
议一议
5 x y
2 0 x 2 y
2 5 a 2 b c 3
典例精析
例3 约分: 1)
1 5 a b 2 c
分析:为约分要先找出分子和分母的公因式. 找公因式方法:
约去系数的最大公约数.
约去分子分母相同因式的最低次幂.
解:
5ac2
3b
1)
25a2bc3 5abc 5ac2
15ab2c 5abc 3b
(公因式是5ac2)
2
x2
2)
9
x 6x 9
x 2
x 2
解: 2)
.
9
x 3
6 x 9
( x 3)( x 3) x 3
( x 3)2
分析:约分时,分子或分母若是多项式,能分解则必须先进行因 式分解.再找出分子和分母的公因式进行约分.
知识要点
约分的基本步骤
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去 相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去 分子﹑分母所有的公因式.
注意事项:
约分前后分式的值要相等.
约分的关键是确定分式的分子和分母的公因式.
约分是对分子、分母的整体进行的,也就是分子的整体和分母的 整体都除以同一个因式.
分式的通分
三
通分:
问题1:
7
1
8
与
1 2
最小公倍数:24
12
解: 7
24
14
12 2
7 2
1
1 3
8 8 3 24
3
分数的通分:把几个异分母的分数化成同分母的分数,而不改变分 数的值,叫做分数的通分.
通分的关键是确定几 个分母的最小公倍数
想一想:
联想分数的通分,由例1你能想出如何对分式进行通分?
a b
a 2 b
=
2
)
2 a - b
a a
2 b
=
(b≠0)
a + b ( a2 + ab )
( 2a b - b2
问题2:填空
知识要点
分式的通分的定义
与分数的通分类似,根据分式的基本性质,使分子、分母同乘适当的 整式(即最简公分母),把分母不相同的分式变成分母相同的分式,
这种变形叫分式的通分.如分式
b
. a b
分后分母都变成了a2b a +
与 分母分别是ab,a2,通
2 a - b
a 2
最简公分母
为通分先要确定各分式的公分母,一般取各分母的所有因式的最高 次幂的积作公分母,叫做最简公分母.
注意:确定最简公母是通分的关键.
3
a b 2 c
a b
(1 ) 与
2 a 2 b
b2
2 a2 c
例4 通分:
,
3bc
3 3 ·bc
= =
2a2b 2a2b ·bc 2a2b2c
2
2
2 2
.
2a b c
a - b (a - b) ·2a 2a2 - 2ab
=
=
ab c ab c ·2a
解:(1)最简公分母是2a2b2c
(2)最简公分母是(x+5)(x-5)
2 x 2 x( x + 5)
2 x2 + 5x
= =
x - 5 ( x - 5)( x + 5)
,
x2 - 25
3x2 - 5x
3x = 3x(x - 5) =
x + 5 (x + 5)(x - 5)
.
x2 - 25
( 2 )
3 x
x 5 x 5
2 x
与
最 简 公 分 母
1·(x-5)
1·(x+5)
1 (x-5) (x+5)
不同的因式
b
a
xy
x 2
y 2
x 2
与
例5 通分:
方法归纳:先将分母因式分解,再将每一个因式看成一个 整体,最后确定最简公分母.
(x+y)(x-y)
解:最简公分母是x(x+y)(x-y)
x(x+y)
,
a a
ax
ax
= =
=
( x - y)( x + y)
x( x - y)( x + y)
x3 - xy 2
x2 - y 2 b
b
b( x - y) bx - by ,
=
= =
x( x + y) x( x - y)( x + y)
x2 + xy x3 - xy 2
确定几个分式的最简公分母的方法:
因式分解
系数:各分式分母系数的最小公倍数;
字母:各分母的所有字母的最高次幂
多项式:各分母所有多项式因式的最高次幂
积
方法归纳
想一想:
分数和分式在约分和通分的做法上有什么共同点?这 些做法的根据是什么?
约分 通分
分数 找分子与分母的 最大公约数 找所有分母的 最小公倍数
分式 找分子与分母的公 因式 找所有分母的 最简公分母
依据 分数或分式的基本性质
当堂练习
D .
x 2
x 2
x 2
a b y 2
4
x y
A . B .
b a
x y
C .
x 2
y 2
2.下列各式中是最简分式的( B )
A.
c c
b a a b
B.
c
c
C.
c c b a a b
D.
a b a b
c
c
b a a b
1.下列各式成立的是( D )
B.不变 D.缩小四倍
y
3.若把分式 x
y 的 x 和y 都扩大两倍,则分式
的值( B ) A.扩大两倍 C.缩小两倍
x y
y中的X和Y都扩大3倍,那么分式
4.若把分式 x
的值( ).
A.扩大3倍 C.扩大4倍
B.扩大9倍 D.不变
解:
ac
a
)
x y
x y
2 ( x
y) y
)
2 bc
x 2
m 2
y 2
1)
ac
; ( 2)
; ( 3 )
x 2
( x y) y
xy 2
1 2bc 2b
m
xy
2 xy
; ( 4 ) m 2 1
5.约分
x y 2
x 2
x
x 2
y 2
3)
x y
x y
(x x y)
( x y)2
m 2
m
4)
.
2 x y
m
m( m 1)
m 1
m 2 1
(1 m )(1 m )
1
3
,
3 a b 3 4 a 2 b
1)
6.通分:
解:最简公分母是12a2b3
1 4 a
=
2
3 a b 3
3
1 2 a 2 b 3
9 b 2
4 a b
1 2 a 2 b 3
=
解:最简公分母是(2x+1)(2x-1)
4 4 ( 2 x + 1 )
8 x + 4
- ( 2 x - 1 ) ( 2 x + 1 )
- 4 x 2 + 1
= =
4
1 2 x
( 2 ) ,
4 x 2 1
2 x
1 - 2 x
2 x
4 x 2 -1
小贴士:在分式的约分与通分中,通常碰到如下因式符号变形:
(b-a)2=(a-b)2;b-a=-(a-b).
( 3 )
x
x 2
2 x y
( x y ) 2
y 2
,
解:最简公分母是(x+y)2(x-y)
2 2
2
2 x y 2
2 x y 2 x y ( x - y )
2 x 2 y -
=
=
( x + y ) ( x + y ) ( x -
y ) ( x + y )
( x - y )
2
2
2
2
y 2
x x ( x + y )
x 2 +
=
=
x - y
( x + y ) ( x -
y ) ( x + y ) ( x - y )
课堂小结
分 式 的 基 本 性 质
内
容
作
用
分式进行约分 和通分的依据
B B C B B C
A A C , A A C
(C 0).
注
意
分子分母同时进行;
分子分母只能同乘或同除,不能进 行同加或同减;
分子分母只能同乘或同除同一个整 式;
除式是不等于零的整式
进行分式运算的基 础
谢谢观看
Thank You
