2021年人教版八年级数学上册15.2.2 第1课时 分式的加减教学课件(28张)
文档属性
| 名称 | 2021年人教版八年级数学上册15.2.2 第1课时 分式的加减教学课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览





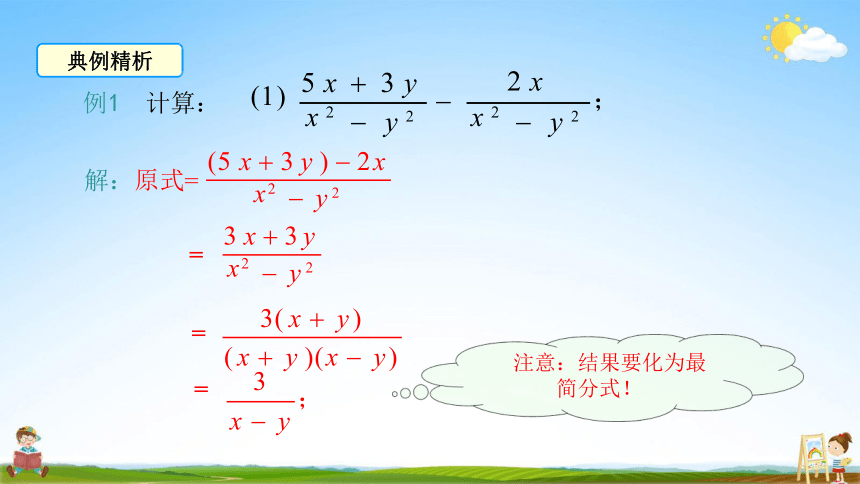


文档简介
(共28张PPT)
第十五章 分式
15.2.2 分式的加减
人教版 数学 八年级 上册
学习目标
掌握分式的加减运算法则并运用其进行计算.(重点)
能够进行异分母的分式加减法运算.(难点)
导入新课
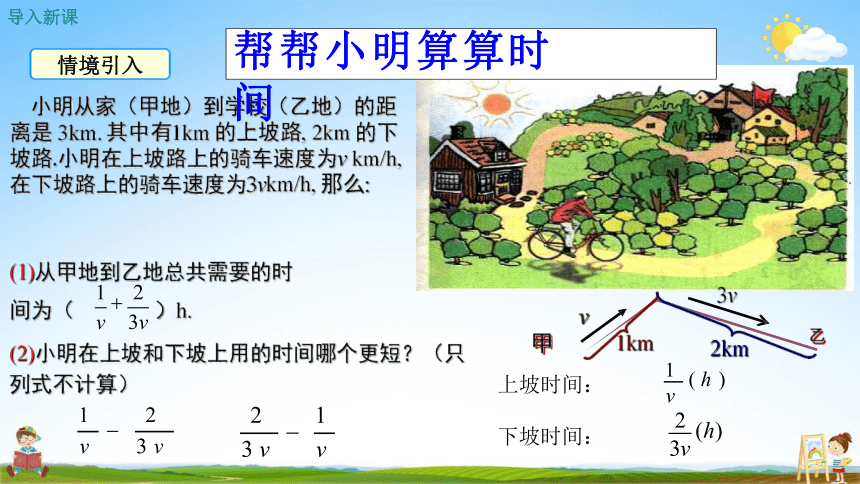
情境引入
3
2v
1
2
v
3 v
2
1
3 v v
1 2
v 3v
上坡时间:
下坡时间:
1 ( h )
v
2 (h)
3v
帮帮小明算算时间
讲授新课
同分母分式的加减
一
类比探究
观察下列分数加减运算的式子,
1 2 1 2 3
5 5 5 5
1 2 1 2 1
5 5 5 5
1 2
a a
1 2
a
1 2
x 2 x 2
1 2
x 2
2
a
x 1 x 1
a 2
x 1
知识要点
同分母分式的加减法则
同分母分式相加减,分母不变,把分子相加减
上述法则可用式子表示为
a b a b .
c c c
x
c
x
y
x
( 1 ) m
y
m a c
y y
( 2 )
d
n
m
2 cab
2 bca
( 3 )
x y
b
x y
2 abc
a
( 4 )
m y c x
m a c y
m n d
2 abc
a b x y
牛刀小试
2 x
x 2
x 2
(1 ) 5 x 3 y
y 2
y 2
;
解:原式=
x 2
(5 x 3 y ) 2 x
y 2
=
=
注意:结果要化为最 简分式!
=
x 2
3 x 3 y
y 2
3( x y )
( x y )( x y )
3
x y
;
典例精析
例1 计算:
( 2 )
.
ab 2
ab 2 ab 2
5 a 2 b 3
3 a 2 b 5
8 a 2 b
解:原式=
(5 a 2 b 3) (3 a 2 b 5 ) (8 a 2 b )
=
ab 2
ab 2
5 a 2 b 3 3a 2 b 5 8 a 2 b
=
2
2 b
a
注意:结果要化为 最简分式!
=
b
ab a
把分子看作一个整 体,先用括号括起 来!
x 2 x 2 x 2
x 2
(1)
x2
x 2 x 2
(2) x 2 x 1 x 3
x 1 x 1 x 1
x 2
4
4
x 2
x 2 x 1 x 3
x 1
注意:当分子是
多项式时要加括号!
注意:结果要化为最 简形式!
x 2 x 1 x 3
x 1
x
x 1
做一做
异分母分式的加减
二
问题: 请计算
1 1
2 3
1 1
2 3
2 3
1 1
6
3 2
6
5
5
6
1
6
3 2
6 6
6
1 1
2 3
3 2
6 6
3 2
6
1
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 .
请计算
3
( 1
2
1
( );
3
2
1 1
1 1
2 3
6
5
6
6 6
3 2
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同 分母的分数,再加减.
1 1
2 3
3 2
6 6
3 2 3 2
6
1
6
1 1
b d
bd
b
bd
d
d b
bd
1 1
b d
b
bd bd
d
d b
bd
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同 分母的分式,再加减.
请思考
5
6
1
6
b
d
b
d
),
bd
d b
bd
d b
知识要点
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
a c ad bc ad bc .
b d bd bd bd
1 )
2 x 1 ;
解:原式=
2
x 1 1 x
x 1
x 1 x 1
=
=
注意:(1-x)=-(x-1)
2 ( x 1)
x 1 3 x ; x 1
例2 计算:
分母不同,先化为同 分母.
1
1
2 p 3 q
2 p 3 q
2 )
;
解:原式=
2 p 3q
2 p 3q
(2 p 3q)(2 p 3q) (2 p 3q)(2 p 3q)
(2 p 3q) (2 p 3q)
(2 p 3q)(2 p 3q) 4 p
(2 p 3q)(2 p 3q) 4 p
4 p2 9q2
先找出最简公分母,再正确通分, 转化为同分母的分式相加减.
x 2
x 2
x 2
x 1
4 x 4
3 )
;
解:原式=
2
2 x
x 2
x 1
x ( x 2 ) ( x 2 )
=
=
注意:分母是多项式先分解 因式
( x 2 )( x 2 )
x ( x 1)
x ( x 2 ) 2
x ( x 2 ) 2
x 2
4 x 2 x x ( x 2 ) 2
先找出最简公分母,再 正确通分,转化为同分 母的分式相加减.
=
x 4
x ( x 2 ) 2
;
知识要点
分式的加减法的思路
通分 转化为
异分母相 加减
同分母
相加减
分子(整式)相 加减
分母不变 转化为
a 2
a 1
a 1
例3.计算: 法一:
a2
(a 1)(a 1)
a 1 a 1
a (a 1)
2 2
a2
a 1
a2 1
1
a 1
法二:
原式
2
a
( a 1 )
a 1
a2
a(a 1) a 1
a 1 a 1 a 1
a2
a 1
a a a a 1
2 2
a 1
a 1
1
a 1
a2
a(a 1) (a 1)
原式
a 1
(a2 a) (a 1)
把整式看成分母为“1” 的分式
=
=
x 2
x 3 2 x 3 2 x 1
1 1 x
x 1 x 1 x 1① x 1
②
③
④
x 3 2 x 1
x 3 2 x 2
= x 1
上述计算过程,从哪一步开始错误,请写出该步的代号 ② ;
错误原因_漏掉了分母;
本题的正确结果为: .
做一做
阅读下面题目的计算过程.
例4 计算:
1
2m
m2
9 m 3
m 3 m 3
m 3 m 3
2 m ( m 3)
解:原式 2 m m 3
从1、-3、3中任选一个你 喜欢的m值代入求值
m 3 m 3
m 3
m 3 m 3
1
m - 3
1-3
当m=1时,原式 1
1
2
1
先化简,再求值:
2
x 2
x 1
1
,其中 x 2 .
解:
1 2
2
x 2
x 1 1
x 1
( x 1)( x 1)
( x 1)( x 1)
x 1
( x 1)( x 1) 1
x 1
1
1
2 1
当x 2时,原式=
做一做
例5 已知下面一列等式:
(1)请你从左边这些等式的结构特征写出它的一般性等式; (2)验证一下你写出的等式是否成立;
(3)利用等式计算:
解析:(1)观察已知的四个等式,发现等式的左边是两个分数 之积,这两个分数的分子都是1,后面一个分数的分母比前面一 个分数的分母大1,并且第一个分数的分母与等式的序号相等, 等式的右边是这两个分数之差,据此可写出一般性等式;
(2)根据分式的运算法则即可验证; (3)根据(1)中的结论求解.
A.
当堂练习
1
a
1 a
a 1
a 1 a 1
B. a
a 1
1. 计算
的结果为(C )
C.-1 D.2
2.填空:
3
5
( 2 )
;
4 x 4 y
x y y x
8
(1) xy ;
xy xy
4
3.计算:
1 2
1 b
a ; 2 .
3a 2b a 1 1 a 2
解:(1)原式=
;
6ab 6ab 6ab
2b2 3a2 2b2 3a2
(2)原式=
1 2
a2
a 1 1
1 2
a 1 a 1 a 1
a 1
a 1 a 1
2
a 1 a 1
a 3 .
a 3
a 1 a 1
a2 1
4.先化简,再求值::
,
其中x=2016.
课堂小结
分式加减运算
加 减 法 运 算
注
意
(1)减式的分式是多项式时,在进行运算时要适 时添加括号
异分母分式相加减先转化为同分 母分式的加减运算
(2)整式和分式之间进行加减运算时,则要把整 式看成分母是1的分式,以便通分
(3)异分母分式进行加减运算需要先通分,关键 是确定最简公分母
谢谢观看
Thank You
第十五章 分式
15.2.2 分式的加减
人教版 数学 八年级 上册
学习目标
掌握分式的加减运算法则并运用其进行计算.(重点)
能够进行异分母的分式加减法运算.(难点)
导入新课
情境引入
3
2v
1
2
v
3 v
2
1
3 v v
1 2
v 3v
上坡时间:
下坡时间:
1 ( h )
v
2 (h)
3v
帮帮小明算算时间
讲授新课
同分母分式的加减
一
类比探究
观察下列分数加减运算的式子,
1 2 1 2 3
5 5 5 5
1 2 1 2 1
5 5 5 5
1 2
a a
1 2
a
1 2
x 2 x 2
1 2
x 2
2
a
x 1 x 1
a 2
x 1
知识要点
同分母分式的加减法则
同分母分式相加减,分母不变,把分子相加减
上述法则可用式子表示为
a b a b .
c c c
x
c
x
y
x
( 1 ) m
y
m a c
y y
( 2 )
d
n
m
2 cab
2 bca
( 3 )
x y
b
x y
2 abc
a
( 4 )
m y c x
m a c y
m n d
2 abc
a b x y
牛刀小试
2 x
x 2
x 2
(1 ) 5 x 3 y
y 2
y 2
;
解:原式=
x 2
(5 x 3 y ) 2 x
y 2
=
=
注意:结果要化为最 简分式!
=
x 2
3 x 3 y
y 2
3( x y )
( x y )( x y )
3
x y
;
典例精析
例1 计算:
( 2 )
.
ab 2
ab 2 ab 2
5 a 2 b 3
3 a 2 b 5
8 a 2 b
解:原式=
(5 a 2 b 3) (3 a 2 b 5 ) (8 a 2 b )
=
ab 2
ab 2
5 a 2 b 3 3a 2 b 5 8 a 2 b
=
2
2 b
a
注意:结果要化为 最简分式!
=
b
ab a
把分子看作一个整 体,先用括号括起 来!
x 2 x 2 x 2
x 2
(1)
x2
x 2 x 2
(2) x 2 x 1 x 3
x 1 x 1 x 1
x 2
4
4
x 2
x 2 x 1 x 3
x 1
注意:当分子是
多项式时要加括号!
注意:结果要化为最 简形式!
x 2 x 1 x 3
x 1
x
x 1
做一做
异分母分式的加减
二
问题: 请计算
1 1
2 3
1 1
2 3
2 3
1 1
6
3 2
6
5
5
6
1
6
3 2
6 6
6
1 1
2 3
3 2
6 6
3 2
6
1
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 .
请计算
3
( 1
2
1
( );
3
2
1 1
1 1
2 3
6
5
6
6 6
3 2
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同 分母的分数,再加减.
1 1
2 3
3 2
6 6
3 2 3 2
6
1
6
1 1
b d
bd
b
bd
d
d b
bd
1 1
b d
b
bd bd
d
d b
bd
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同 分母的分式,再加减.
请思考
5
6
1
6
b
d
b
d
),
bd
d b
bd
d b
知识要点
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
a c ad bc ad bc .
b d bd bd bd
1 )
2 x 1 ;
解:原式=
2
x 1 1 x
x 1
x 1 x 1
=
=
注意:(1-x)=-(x-1)
2 ( x 1)
x 1 3 x ; x 1
例2 计算:
分母不同,先化为同 分母.
1
1
2 p 3 q
2 p 3 q
2 )
;
解:原式=
2 p 3q
2 p 3q
(2 p 3q)(2 p 3q) (2 p 3q)(2 p 3q)
(2 p 3q) (2 p 3q)
(2 p 3q)(2 p 3q) 4 p
(2 p 3q)(2 p 3q) 4 p
4 p2 9q2
先找出最简公分母,再正确通分, 转化为同分母的分式相加减.
x 2
x 2
x 2
x 1
4 x 4
3 )
;
解:原式=
2
2 x
x 2
x 1
x ( x 2 ) ( x 2 )
=
=
注意:分母是多项式先分解 因式
( x 2 )( x 2 )
x ( x 1)
x ( x 2 ) 2
x ( x 2 ) 2
x 2
4 x 2 x x ( x 2 ) 2
先找出最简公分母,再 正确通分,转化为同分 母的分式相加减.
=
x 4
x ( x 2 ) 2
;
知识要点
分式的加减法的思路
通分 转化为
异分母相 加减
同分母
相加减
分子(整式)相 加减
分母不变 转化为
a 2
a 1
a 1
例3.计算: 法一:
a2
(a 1)(a 1)
a 1 a 1
a (a 1)
2 2
a2
a 1
a2 1
1
a 1
法二:
原式
2
a
( a 1 )
a 1
a2
a(a 1) a 1
a 1 a 1 a 1
a2
a 1
a a a a 1
2 2
a 1
a 1
1
a 1
a2
a(a 1) (a 1)
原式
a 1
(a2 a) (a 1)
把整式看成分母为“1” 的分式
=
=
x 2
x 3 2 x 3 2 x 1
1 1 x
x 1 x 1 x 1① x 1
②
③
④
x 3 2 x 1
x 3 2 x 2
= x 1
上述计算过程,从哪一步开始错误,请写出该步的代号 ② ;
错误原因_漏掉了分母;
本题的正确结果为: .
做一做
阅读下面题目的计算过程.
例4 计算:
1
2m
m2
9 m 3
m 3 m 3
m 3 m 3
2 m ( m 3)
解:原式 2 m m 3
从1、-3、3中任选一个你 喜欢的m值代入求值
m 3 m 3
m 3
m 3 m 3
1
m - 3
1-3
当m=1时,原式 1
1
2
1
先化简,再求值:
2
x 2
x 1
1
,其中 x 2 .
解:
1 2
2
x 2
x 1 1
x 1
( x 1)( x 1)
( x 1)( x 1)
x 1
( x 1)( x 1) 1
x 1
1
1
2 1
当x 2时,原式=
做一做
例5 已知下面一列等式:
(1)请你从左边这些等式的结构特征写出它的一般性等式; (2)验证一下你写出的等式是否成立;
(3)利用等式计算:
解析:(1)观察已知的四个等式,发现等式的左边是两个分数 之积,这两个分数的分子都是1,后面一个分数的分母比前面一 个分数的分母大1,并且第一个分数的分母与等式的序号相等, 等式的右边是这两个分数之差,据此可写出一般性等式;
(2)根据分式的运算法则即可验证; (3)根据(1)中的结论求解.
A.
当堂练习
1
a
1 a
a 1
a 1 a 1
B. a
a 1
1. 计算
的结果为(C )
C.-1 D.2
2.填空:
3
5
( 2 )
;
4 x 4 y
x y y x
8
(1) xy ;
xy xy
4
3.计算:
1 2
1 b
a ; 2 .
3a 2b a 1 1 a 2
解:(1)原式=
;
6ab 6ab 6ab
2b2 3a2 2b2 3a2
(2)原式=
1 2
a2
a 1 1
1 2
a 1 a 1 a 1
a 1
a 1 a 1
2
a 1 a 1
a 3 .
a 3
a 1 a 1
a2 1
4.先化简,再求值::
,
其中x=2016.
课堂小结
分式加减运算
加 减 法 运 算
注
意
(1)减式的分式是多项式时,在进行运算时要适 时添加括号
异分母分式相加减先转化为同分 母分式的加减运算
(2)整式和分式之间进行加减运算时,则要把整 式看成分母是1的分式,以便通分
(3)异分母分式进行加减运算需要先通分,关键 是确定最简公分母
谢谢观看
Thank You
