2021年人教版八年级数学上册15.2.3 整数指数幂教学课件(29张)
文档属性
| 名称 | 2021年人教版八年级数学上册15.2.3 整数指数幂教学课件(29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览








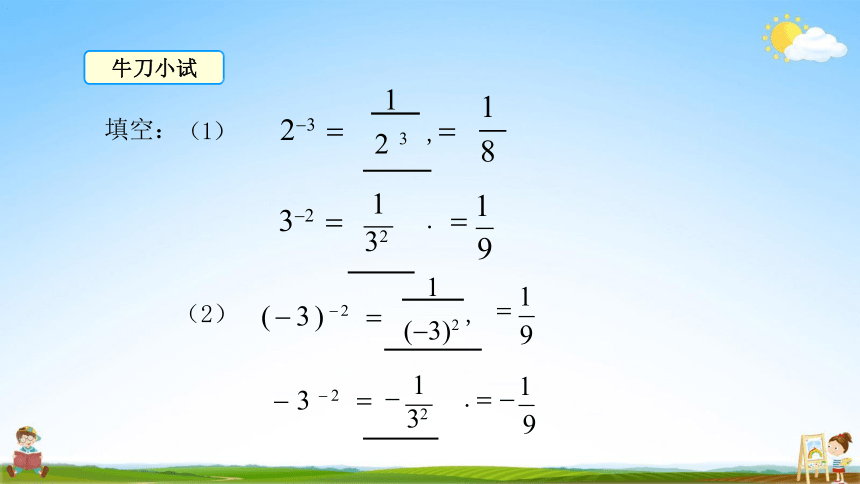
文档简介
(共29张PPT)
第十五章 分式
15.2.3 整数指数幂
人教版 数学 八年级 上册
学习目标
1.理解并掌握整数指数幂的运算性质
会用科学记数法表示绝对值小于1的数.(重点)
3.理解负整数指数幂的性质并应用其解决实际问题.(难点)
导入新课
问题引入
算一算,并分别说出每一小题所用的运算性质.
(x4 )3
=
同底数幂的乘法:
a n
(m,n是正整数)
a m a m n
x 1 2
( a m ) n
a m n
(m,n是正整数)
=
;
(3) (xy)3
积的乘方:
x 3 y 3
( a b ) n
a n b n
(n是正整数)
(2)
幂的乘方:
算一算,并分别说出每一小题所用的运算性质.
同底数幂的除法: a m
a n
a m n
(a≠0,m,n是正整数且m>n )
(4)a 4 a=3 a ;
;
a3
b3
n
a
a n
商的乘方:( )
b
b n
(b≠0,n是正整数)
(5) (
)3 =
a b
a 0
(6)x 4
x 4= 1 ;
1 (
a )0
想一想:
am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表 示什么?
讲授新课
负整数指数幂
一
问题:计算:a3 ÷a5= (a ≠0)
解法1
3
5
1
a 3 a 3
.
a 2
a a
a 5 a 2 a 3
解法2 再假设正整数指数幂的运算性质 am÷an=amn(a≠0,m,n是正整数,m>n)中的m>n这个条件去 掉,那么a3÷a5=a3-5=a-2.
于是得到:
1
.
a 2
a 2
知识要点
负整数指数幂的意义
一般地,我们规定:当n是正整数时,
an
a n 1
(a 0)
这就是说,a-n (a≠0)是an的倒数.
引入负整数指数幂后,指数的取值范围就推广到全体整数. 也就说前面提到的运算性质也推广到整数指数幂.
想一想:对于am,当m=7,0,-7时,你能分别说出它们的意义吗?
(2)
2 3
( 3 ) 2
32
. 1
9
3 2
1
3 2
2 3
8
1
1
,
32
1
9
. 1
1
,
( 3)2
1
9
牛刀小试
填空:(1)
例1
A.a>b=c C.c>a>b
B.a>c>b D.b>c>a
典例精析
B
方法总结:关键是理解负整数指数幂的意义,依次计算出 结果.当底数是分数时,只要把分子、分母颠倒,负指数 就可变为正指数.
计算:
(1)(x3y-2)2; (2)x2y-2·(x-2y)3;
例2
解析:先进行幂的乘方,再进行幂的乘除,最后将整数指 数幂化成正整数指数幂.
解:(1)原式=x6y-4
(2)原式=x2y-2·x-6y3=x-4y
提示:计算结果一般需化为正整数幂的形式.
例2 计 算 : (3)(3x2y-2)2÷(x-2y)3; (4)(3×10-5)3÷(3×10-6)2.
解:(3)原式=9x4y-4÷x-6y3
=9x4y-4·x6y-3
=9x10y-7
(4)原式=(27×10-15)÷(9×10-12)
=3×10-3
计算:
(3) (a 1b2 )3 ; (4)
b3 2
(1) a 2 a5 ;
(2) ;
a2
a 2b2 (a2b 2 ) 3.
解:
(1)
a7
a 2 a5 a 2 5 a 7 1 ;
4
3
2
6
;
b
b
a
a
a
b
6
2
4
)
2 ) (
做一做
解:
;
b 6
a 3
1 2 3
3 6
( 3 ) ( a b ) a b
2
8
8
)
.
b
a
2 b 2
( a 2 b 2 3
6 b 6
8
8
( 4 ) a
a 2 b a
a b
(3) (a 1b2 )3 ; (4)
a 2b2 (a2b 2 ) 3.
(1) 根据整数指数幂的运算性质,当m,n为整数时,
am ÷an=am-n
又am ·a-n=am-n,因此am ÷an=am ·a-n.
即同底数幂的除法可以转化为同底数幂的乘法.
(2) 特别地,
a
n 1 n n n
所以 ( ) ( a b ) a b ,
b
即商的乘方可以转化为积的乘方.
总结归纳
a b
=a÷b=
axb 1
整数指数幂的运算性质归结为
am·an=am+n ( m、n是整数) ; (2)(am)n=amn ( m、n是整数) ; (3)(ab)n=anbn ( n是整数).
例3
解析:分别根据有理数的乘方、0指数幂、负整数指数幂及绝 对值的性质计算出各数,再根据实数的运算法则进行计算.
科学记数法
二
忆一忆:
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是 正整数.
例如,864000可以写成 8.64×105 .
想一想:
怎样把0.0000864用科学记数法表示?
探一探: 因为
;
0 .0 1
所以, 0.0000864=8.64 ×0.00001=8.64 ×10-5.
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些 绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整 数 ,1≤∣ a∣ <10.
1
1 0 0
10-2
1
10-3
0.001
0.1 1 10 1;
10
1 0 0 0
算一算:
10-2=
;
0_.0_1 ; 10-4= 0.0001
10-8= 0_._0_0_0_0_0_0_0_1 .
议一议:
指数与运算结果的0的个数有什么关系? 通过上面的探索,你发现了什么?:
一般地,10的-n次幂,在1前面有 n 个0.
想一想:10-21的小数点后的位数是几位?1前面有几个零?
用科学记数法表示一些绝对值小于1的数的方法:
即利用10的负整数次幂,把一个绝对值小于1的数表示成a×10-n的形 式,其中n是正整数,1 ≤ ︴a ︴<10. n等于原数第一个非零数字前所 有零的个数(特别注意:包括小数点前面这个零).
知识要点
例4 用小数表示下列各数: (1)2×10-7;(2)3.14×10-5; (3)7.08×10-3;(4)2.17×10-1.
解析:小数点向左移动相应的位数即可. 解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708; (4)2.17×10-1=0.217.
1.用科学记数法表示:
(2)-0.000 006 4;
(1)0.000 03;
(3)0.000 0314;
2.用科学记数法填空:
(1)1 s是1 μs的1 000 000倍,则1 μs= s;
(2)1 mg= kg;(3)1 μm = m;
(4)1 nm= μm ;(5)1 cm2= m2 ;
(6)1 ml = m3.
练一练
例5 纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球 上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物 体(物体之间隙忽略不计)?
1mm 10 3 m,1nm 10 9 m.
典例精析
(10 3 )3 (10 9 )3 10 9 10 27 1018
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1 亿(即108)的100亿(即1010) 倍.
当堂练习
1.填空:(-3)2·(-3)-2=( 1 );103×10-2=( 10 );
2
1
0.1
0.11 3 0.1 2
100
25
(2)(-5)2 008÷(-5)2 010 ( 5)2 008 2 010 ( 5) 2
1 1
( 5)2
10 102 10
(3)100×10-1÷10-2 1 1 1 1 100 10
a-2÷a3=( 1 );a3÷a-4=( a7 ).
a5
2.计算:(1)0.1÷0.13
计算:
(1)(2×10-6)× (3.2×103)= 6.4×10-3;
(2)(2×10-6)2 ÷ (10-4)3. = 4
下列是用科学记数法表示的数,写出原来的数.
(1)2×10-8 (2)7.001×10-6
答案:(1)0.000 000 02 (2)0.000 007 001
5.比较大小:
(1)3.01×10-4 < 9.5×10-3
(2)3.01×10-4 < 3.10×10-4
6.用科学记数法把0.000 009 405表示成
9.405×10n,那么n= -6 .
课堂小结
整数指数幂运 算
整 指
数
数 幂
零指数幂:当a≠0时,a0=1.
负整数指数幂:当n是正整数时,a-n=
an
1 (a≠0)
整数指数幂的运算性质:
(1)am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
用科学记数法表 示绝对值小于1的 数
绝对值小于1的数用科学记数法表示为a×10-n的形式,
1≤│a│ <10,n为原数第1个不为0的数字前面所有0的个数
(包括小数点前面那个0).
谢谢观看
Thank You
第十五章 分式
15.2.3 整数指数幂
人教版 数学 八年级 上册
学习目标
1.理解并掌握整数指数幂的运算性质
会用科学记数法表示绝对值小于1的数.(重点)
3.理解负整数指数幂的性质并应用其解决实际问题.(难点)
导入新课
问题引入
算一算,并分别说出每一小题所用的运算性质.
(x4 )3
=
同底数幂的乘法:
a n
(m,n是正整数)
a m a m n
x 1 2
( a m ) n
a m n
(m,n是正整数)
=
;
(3) (xy)3
积的乘方:
x 3 y 3
( a b ) n
a n b n
(n是正整数)
(2)
幂的乘方:
算一算,并分别说出每一小题所用的运算性质.
同底数幂的除法: a m
a n
a m n
(a≠0,m,n是正整数且m>n )
(4)a 4 a=3 a ;
;
a3
b3
n
a
a n
商的乘方:( )
b
b n
(b≠0,n是正整数)
(5) (
)3 =
a b
a 0
(6)x 4
x 4= 1 ;
1 (
a )0
想一想:
am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表 示什么?
讲授新课
负整数指数幂
一
问题:计算:a3 ÷a5= (a ≠0)
解法1
3
5
1
a 3 a 3
.
a 2
a a
a 5 a 2 a 3
解法2 再假设正整数指数幂的运算性质 am÷an=amn(a≠0,m,n是正整数,m>n)中的m>n这个条件去 掉,那么a3÷a5=a3-5=a-2.
于是得到:
1
.
a 2
a 2
知识要点
负整数指数幂的意义
一般地,我们规定:当n是正整数时,
an
a n 1
(a 0)
这就是说,a-n (a≠0)是an的倒数.
引入负整数指数幂后,指数的取值范围就推广到全体整数. 也就说前面提到的运算性质也推广到整数指数幂.
想一想:对于am,当m=7,0,-7时,你能分别说出它们的意义吗?
(2)
2 3
( 3 ) 2
32
. 1
9
3 2
1
3 2
2 3
8
1
1
,
32
1
9
. 1
1
,
( 3)2
1
9
牛刀小试
填空:(1)
例1
A.a>b=c C.c>a>b
B.a>c>b D.b>c>a
典例精析
B
方法总结:关键是理解负整数指数幂的意义,依次计算出 结果.当底数是分数时,只要把分子、分母颠倒,负指数 就可变为正指数.
计算:
(1)(x3y-2)2; (2)x2y-2·(x-2y)3;
例2
解析:先进行幂的乘方,再进行幂的乘除,最后将整数指 数幂化成正整数指数幂.
解:(1)原式=x6y-4
(2)原式=x2y-2·x-6y3=x-4y
提示:计算结果一般需化为正整数幂的形式.
例2 计 算 : (3)(3x2y-2)2÷(x-2y)3; (4)(3×10-5)3÷(3×10-6)2.
解:(3)原式=9x4y-4÷x-6y3
=9x4y-4·x6y-3
=9x10y-7
(4)原式=(27×10-15)÷(9×10-12)
=3×10-3
计算:
(3) (a 1b2 )3 ; (4)
b3 2
(1) a 2 a5 ;
(2) ;
a2
a 2b2 (a2b 2 ) 3.
解:
(1)
a7
a 2 a5 a 2 5 a 7 1 ;
4
3
2
6
;
b
b
a
a
a
b
6
2
4
)
2 ) (
做一做
解:
;
b 6
a 3
1 2 3
3 6
( 3 ) ( a b ) a b
2
8
8
)
.
b
a
2 b 2
( a 2 b 2 3
6 b 6
8
8
( 4 ) a
a 2 b a
a b
(3) (a 1b2 )3 ; (4)
a 2b2 (a2b 2 ) 3.
(1) 根据整数指数幂的运算性质,当m,n为整数时,
am ÷an=am-n
又am ·a-n=am-n,因此am ÷an=am ·a-n.
即同底数幂的除法可以转化为同底数幂的乘法.
(2) 特别地,
a
n 1 n n n
所以 ( ) ( a b ) a b ,
b
即商的乘方可以转化为积的乘方.
总结归纳
a b
=a÷b=
axb 1
整数指数幂的运算性质归结为
am·an=am+n ( m、n是整数) ; (2)(am)n=amn ( m、n是整数) ; (3)(ab)n=anbn ( n是整数).
例3
解析:分别根据有理数的乘方、0指数幂、负整数指数幂及绝 对值的性质计算出各数,再根据实数的运算法则进行计算.
科学记数法
二
忆一忆:
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是 正整数.
例如,864000可以写成 8.64×105 .
想一想:
怎样把0.0000864用科学记数法表示?
探一探: 因为
;
0 .0 1
所以, 0.0000864=8.64 ×0.00001=8.64 ×10-5.
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些 绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整 数 ,1≤∣ a∣ <10.
1
1 0 0
10-2
1
10-3
0.001
0.1 1 10 1;
10
1 0 0 0
算一算:
10-2=
;
0_.0_1 ; 10-4= 0.0001
10-8= 0_._0_0_0_0_0_0_0_1 .
议一议:
指数与运算结果的0的个数有什么关系? 通过上面的探索,你发现了什么?:
一般地,10的-n次幂,在1前面有 n 个0.
想一想:10-21的小数点后的位数是几位?1前面有几个零?
用科学记数法表示一些绝对值小于1的数的方法:
即利用10的负整数次幂,把一个绝对值小于1的数表示成a×10-n的形 式,其中n是正整数,1 ≤ ︴a ︴<10. n等于原数第一个非零数字前所 有零的个数(特别注意:包括小数点前面这个零).
知识要点
例4 用小数表示下列各数: (1)2×10-7;(2)3.14×10-5; (3)7.08×10-3;(4)2.17×10-1.
解析:小数点向左移动相应的位数即可. 解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708; (4)2.17×10-1=0.217.
1.用科学记数法表示:
(2)-0.000 006 4;
(1)0.000 03;
(3)0.000 0314;
2.用科学记数法填空:
(1)1 s是1 μs的1 000 000倍,则1 μs= s;
(2)1 mg= kg;(3)1 μm = m;
(4)1 nm= μm ;(5)1 cm2= m2 ;
(6)1 ml = m3.
练一练
例5 纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球 上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物 体(物体之间隙忽略不计)?
1mm 10 3 m,1nm 10 9 m.
典例精析
(10 3 )3 (10 9 )3 10 9 10 27 1018
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1 亿(即108)的100亿(即1010) 倍.
当堂练习
1.填空:(-3)2·(-3)-2=( 1 );103×10-2=( 10 );
2
1
0.1
0.11 3 0.1 2
100
25
(2)(-5)2 008÷(-5)2 010 ( 5)2 008 2 010 ( 5) 2
1 1
( 5)2
10 102 10
(3)100×10-1÷10-2 1 1 1 1 100 10
a-2÷a3=( 1 );a3÷a-4=( a7 ).
a5
2.计算:(1)0.1÷0.13
计算:
(1)(2×10-6)× (3.2×103)= 6.4×10-3;
(2)(2×10-6)2 ÷ (10-4)3. = 4
下列是用科学记数法表示的数,写出原来的数.
(1)2×10-8 (2)7.001×10-6
答案:(1)0.000 000 02 (2)0.000 007 001
5.比较大小:
(1)3.01×10-4 < 9.5×10-3
(2)3.01×10-4 < 3.10×10-4
6.用科学记数法把0.000 009 405表示成
9.405×10n,那么n= -6 .
课堂小结
整数指数幂运 算
整 指
数
数 幂
零指数幂:当a≠0时,a0=1.
负整数指数幂:当n是正整数时,a-n=
an
1 (a≠0)
整数指数幂的运算性质:
(1)am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
用科学记数法表 示绝对值小于1的 数
绝对值小于1的数用科学记数法表示为a×10-n的形式,
1≤│a│ <10,n为原数第1个不为0的数字前面所有0的个数
(包括小数点前面那个0).
谢谢观看
Thank You
