京改版七下数学7.7几种简单几何图形及其推理2.对顶角教学设计(表格式)
文档属性
| 名称 | 京改版七下数学7.7几种简单几何图形及其推理2.对顶角教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 78.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 04:56:53 | ||
图片预览

文档简介
对顶角教学设计
教学基本信息
课题 7.7几种简单几何图形及其推理(二)
学科 数学 学段 第三学段 年级 七年级 学期 第二学期
相关领域 图形与几何
教材 教科书名称:义务教育教科书 数学 七年级下册 出版社:北京出版集团公司北京出版社 出版日期:2016年1月
单位 设计人
一、教学背景分析
【教学内容分析】 对顶角是七年级下册第七章第四小节的内容.七年级上册第三章具体的介绍了角的定义及其分类、角的度量与换算、角平分线.本节课是在学生已有知识和经验的基础上,继续从观察与实验、归纳与类比、猜想与证明这种人们认识事物方法的角度研究对顶角.从知识角度,对顶角是后续学习平行线的性质与判定的基础.从方法角度,由归纳、猜想到证明,由感性认识到理性认识,即运用逻辑的方法,帮助学生从困惑中走出来. 【学情分析】 学生在上学期已经学习了角的定义及其分类、角的度量与换算、角平分线.在本章的学习中学生了解了认识事物的方法,推理相关的概念.本节课学生要进入更高层次推理实践,学生会感到不适应.所以本节课将从观察身边的实物图形,到画一画,最后归纳、猜想、证明来研究对顶角的性质.在研究过程中从熟悉的事例出发,注重几何直观,培养学生思考问题更加严谨,更富逻辑性.
二、教学目标
1.理解对顶角的概念,掌握对顶角的性质.会利用对顶角的概念与性质解决简单的几何问题. 2.在观察、归纳、猜想、证明对顶角相等的过程中,树立等角转化思想,培养逻辑思维能力. 3.在数学活动中经历探索对顶角性质的过程,培养勇于实践探索的精神,发展有条理的思考与表达.
三、教学重、难点
教学重点:对顶角的概念与性质. 教学难点:对顶角性质的证明的书写格式.
四、教学过程及分析
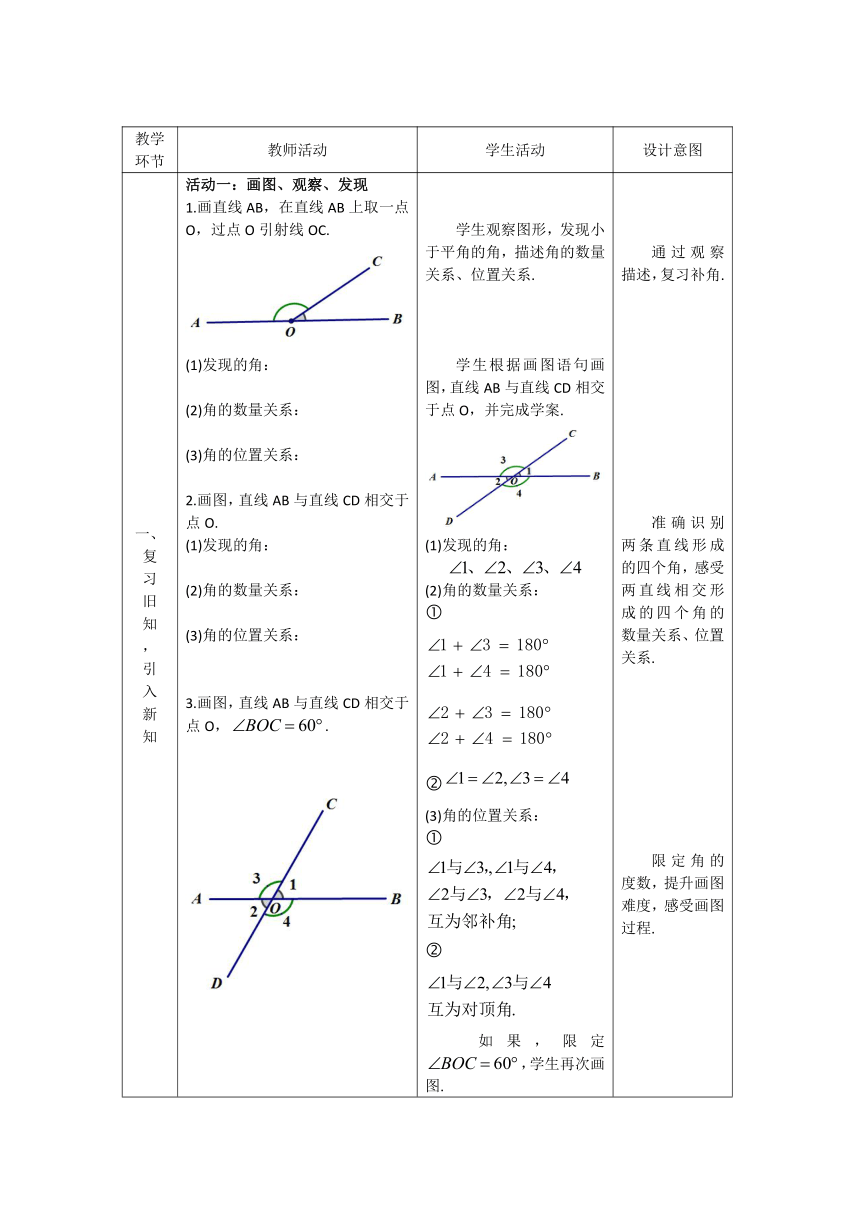
教学 环节 教师活动 学生活动 设计意图
一、 复 习 旧 知 , 引 入 新 知 活动一:画图、观察、发现 画直线AB,在直线AB上取一点O,过点O引射线OC. 发现的角: 角的数量关系: 角的位置关系: 画图,直线AB与直线CD相交于点O. 发现的角: 角的数量关系: (3)角的位置关系: 画图,直线AB与直线CD相交于点O,. 学生观察图形,发现小于平角的角,描述角的数量关系、位置关系. 学生根据画图语句画图,直线AB与直线CD相交于点O,并完成学案. (1)发现的角: (2)角的数量关系: 角的位置关系: 如果,限定 ,学生再次画图. 通过观察描述,复习补角. 准确识别两条直线形成的四个角,感受两直线相交形成的四个角的数量关系、位置关系. 限定角的度数,提升画图难度,感受画图过程.
二、 理 解 概 念 , 提 出 问 题 活动二:生成对顶角的定义 仍然是对顶角.那么怎么定义对顶角? 2.回忆画图的过程,在画图的时候先画的是谁,再怎么画? 3.你们先画的是,再沿着的顶点反向延长的两边,得到了的对顶角,结合画图过程,该怎么定义对顶角呢? 如果两个角有公共的顶点,并且其中一个角的两边分别是另一个角的两边的反向延长线,那么称这两个角互为对顶角. 4.回到图中,对顶角与度数都是,怎么证明呢? 学生回忆画图过程,先画一个角,再沿着已画的角的顶点反向延长,即可得到想要的图形. 学生试着用自己的语言总结对顶角的定义. 学生由补角、及,说明. 帮助学生分析图形的结构,从而引出对顶角的定义.培养总结概括能力,和语言表达能力. 由特殊角证明对顶角相等的方法,引出一般角的证明.
三、 寻 找 方 法 , 解 决 问 题 活动三:探究对顶角的性质 1. 若不知的度数,变化图形, 与的数量关系会不会发生变化? 已知:直线AB,CD相交于点O 求证 证明:是直线(已知) (平角的定义) 是直线(已知) (平角的定义) (同角的补角相等) 对顶角的性质:对顶角相等. 条件(位置关系):∠1和∠2是对顶角 结论(数量关系):∠1=∠2 符号语言: 直线AB,CD相交于点O, ∠1=∠2. 例题讲解 结合图形,直线AB,直线CD相交于点O,你想到了什么?只想到了对顶角吗?还能想到什么? 对应的,你能说出题中每一句话对应的图形及你的发现吗? 要想求∠BOD的度数,应以图中哪个角为过渡,建立什么样的联系? 5.变式训练, 变式1 如例题图,直线AB、直线CD相交于点O,OE⊥AB于点O,∠BOD=35°,求∠COE的度数? 变式2 如例题图,直线AB、直线CD相交于点O,OE⊥AB于点O,与有何数量关系? 变式3 如例题图,直线AB、直线CD相交于点O,∠COE=55°,∠BOD=35°,求证:OE⊥AB于点O. 变式4 直线AB、直线CD相交于点O,OE⊥AB于点O,∠COE=55°,求∠BOD的度数。 学生说理对于更一般的情况该怎么证明. 学生读题,先结合学案独立分析题意,再合作交流分析怎么求角的. 例.如图,直线AB,直线CD相交于点O,OE⊥AB于点O,∠COE=55°,求∠BOD的度数. 学生说一说,题变形之后怎么求角. 特殊到一般,说理证明方法.培养逻辑推理能力和语言表达能力. 通过变式训练,加深利用对顶角的性质解决简单几何问题的理解.
四、 课 堂 小 结 1.回忆,这节课我们都学到了什么知识? 2.我们是从哪些角度来研究相交直线所成图形中的角? 3.由位置关系“相交直线所得的对顶角”得到数量关系“对顶角相等”,反过来由两个角相等能得到它们互为对顶角吗? 对顶角的定义 对顶角的性质 及其推导过程 认识事物的方法 形成新知识对顶角的逻辑体系.感受认识事物的过程.
五、 板 书 设 计 对顶角 一、定义 关键词:公共的顶点、 反向延长线 二、性质 对顶角相等 直线AB,CD相交于点O, ∠1=∠2.
教学基本信息
课题 7.7几种简单几何图形及其推理(二)
学科 数学 学段 第三学段 年级 七年级 学期 第二学期
相关领域 图形与几何
教材 教科书名称:义务教育教科书 数学 七年级下册 出版社:北京出版集团公司北京出版社 出版日期:2016年1月
单位 设计人
一、教学背景分析
【教学内容分析】 对顶角是七年级下册第七章第四小节的内容.七年级上册第三章具体的介绍了角的定义及其分类、角的度量与换算、角平分线.本节课是在学生已有知识和经验的基础上,继续从观察与实验、归纳与类比、猜想与证明这种人们认识事物方法的角度研究对顶角.从知识角度,对顶角是后续学习平行线的性质与判定的基础.从方法角度,由归纳、猜想到证明,由感性认识到理性认识,即运用逻辑的方法,帮助学生从困惑中走出来. 【学情分析】 学生在上学期已经学习了角的定义及其分类、角的度量与换算、角平分线.在本章的学习中学生了解了认识事物的方法,推理相关的概念.本节课学生要进入更高层次推理实践,学生会感到不适应.所以本节课将从观察身边的实物图形,到画一画,最后归纳、猜想、证明来研究对顶角的性质.在研究过程中从熟悉的事例出发,注重几何直观,培养学生思考问题更加严谨,更富逻辑性.
二、教学目标
1.理解对顶角的概念,掌握对顶角的性质.会利用对顶角的概念与性质解决简单的几何问题. 2.在观察、归纳、猜想、证明对顶角相等的过程中,树立等角转化思想,培养逻辑思维能力. 3.在数学活动中经历探索对顶角性质的过程,培养勇于实践探索的精神,发展有条理的思考与表达.
三、教学重、难点
教学重点:对顶角的概念与性质. 教学难点:对顶角性质的证明的书写格式.
四、教学过程及分析
教学 环节 教师活动 学生活动 设计意图
一、 复 习 旧 知 , 引 入 新 知 活动一:画图、观察、发现 画直线AB,在直线AB上取一点O,过点O引射线OC. 发现的角: 角的数量关系: 角的位置关系: 画图,直线AB与直线CD相交于点O. 发现的角: 角的数量关系: (3)角的位置关系: 画图,直线AB与直线CD相交于点O,. 学生观察图形,发现小于平角的角,描述角的数量关系、位置关系. 学生根据画图语句画图,直线AB与直线CD相交于点O,并完成学案. (1)发现的角: (2)角的数量关系: 角的位置关系: 如果,限定 ,学生再次画图. 通过观察描述,复习补角. 准确识别两条直线形成的四个角,感受两直线相交形成的四个角的数量关系、位置关系. 限定角的度数,提升画图难度,感受画图过程.
二、 理 解 概 念 , 提 出 问 题 活动二:生成对顶角的定义 仍然是对顶角.那么怎么定义对顶角? 2.回忆画图的过程,在画图的时候先画的是谁,再怎么画? 3.你们先画的是,再沿着的顶点反向延长的两边,得到了的对顶角,结合画图过程,该怎么定义对顶角呢? 如果两个角有公共的顶点,并且其中一个角的两边分别是另一个角的两边的反向延长线,那么称这两个角互为对顶角. 4.回到图中,对顶角与度数都是,怎么证明呢? 学生回忆画图过程,先画一个角,再沿着已画的角的顶点反向延长,即可得到想要的图形. 学生试着用自己的语言总结对顶角的定义. 学生由补角、及,说明. 帮助学生分析图形的结构,从而引出对顶角的定义.培养总结概括能力,和语言表达能力. 由特殊角证明对顶角相等的方法,引出一般角的证明.
三、 寻 找 方 法 , 解 决 问 题 活动三:探究对顶角的性质 1. 若不知的度数,变化图形, 与的数量关系会不会发生变化? 已知:直线AB,CD相交于点O 求证 证明:是直线(已知) (平角的定义) 是直线(已知) (平角的定义) (同角的补角相等) 对顶角的性质:对顶角相等. 条件(位置关系):∠1和∠2是对顶角 结论(数量关系):∠1=∠2 符号语言: 直线AB,CD相交于点O, ∠1=∠2. 例题讲解 结合图形,直线AB,直线CD相交于点O,你想到了什么?只想到了对顶角吗?还能想到什么? 对应的,你能说出题中每一句话对应的图形及你的发现吗? 要想求∠BOD的度数,应以图中哪个角为过渡,建立什么样的联系? 5.变式训练, 变式1 如例题图,直线AB、直线CD相交于点O,OE⊥AB于点O,∠BOD=35°,求∠COE的度数? 变式2 如例题图,直线AB、直线CD相交于点O,OE⊥AB于点O,与有何数量关系? 变式3 如例题图,直线AB、直线CD相交于点O,∠COE=55°,∠BOD=35°,求证:OE⊥AB于点O. 变式4 直线AB、直线CD相交于点O,OE⊥AB于点O,∠COE=55°,求∠BOD的度数。 学生说理对于更一般的情况该怎么证明. 学生读题,先结合学案独立分析题意,再合作交流分析怎么求角的. 例.如图,直线AB,直线CD相交于点O,OE⊥AB于点O,∠COE=55°,求∠BOD的度数. 学生说一说,题变形之后怎么求角. 特殊到一般,说理证明方法.培养逻辑推理能力和语言表达能力. 通过变式训练,加深利用对顶角的性质解决简单几何问题的理解.
四、 课 堂 小 结 1.回忆,这节课我们都学到了什么知识? 2.我们是从哪些角度来研究相交直线所成图形中的角? 3.由位置关系“相交直线所得的对顶角”得到数量关系“对顶角相等”,反过来由两个角相等能得到它们互为对顶角吗? 对顶角的定义 对顶角的性质 及其推导过程 认识事物的方法 形成新知识对顶角的逻辑体系.感受认识事物的过程.
五、 板 书 设 计 对顶角 一、定义 关键词:公共的顶点、 反向延长线 二、性质 对顶角相等 直线AB,CD相交于点O, ∠1=∠2.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
