青岛版七下数学13.2.2多边形的内角和与外角和 课件(23张ppt)
文档属性
| 名称 | 青岛版七下数学13.2.2多边形的内角和与外角和 课件(23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 290.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
青岛2011课标版 《数学》七年级下册
13.2.2多边形的内角和与外角和
一.问题:
问题1:我们学过哪些几何图形的内角和?
三角形内角和为180°
正方形内角和为360°
那么,任意一个四边形的内角和等于360°?
长方形内角和为360°
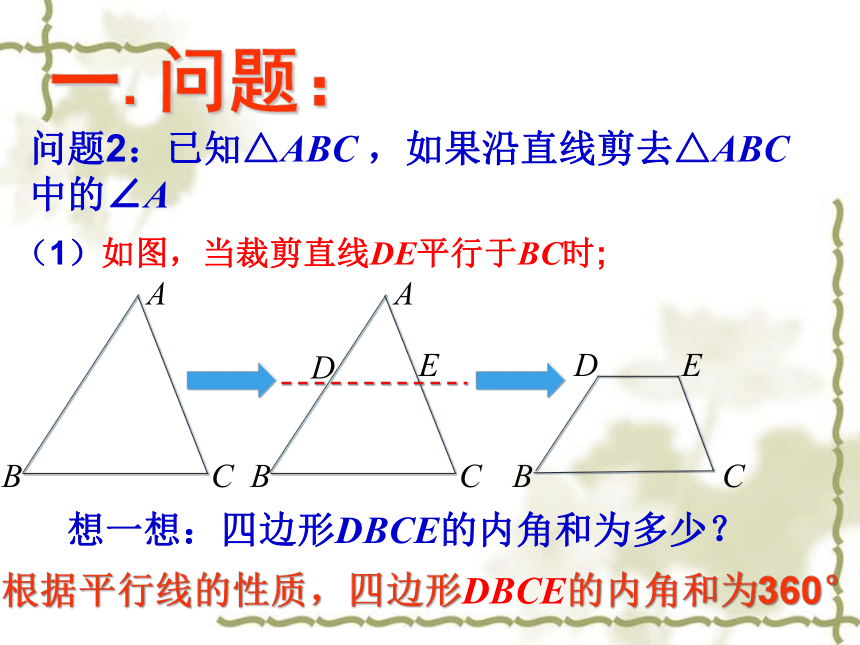
问题2:已知△ABC ,如果沿直线剪去△ABC 中的∠A
A
B
C
A
B
C
D
E
B
C
D
E
(1)如图,当裁剪直线DE平行于BC时;
根据平行线的性质,四边形DBCE的内角和为360°
一.问题:
想一想:四边形DBCE的内角和为多少?
A
B
C
A
B
C
D
E
B
C
D
E
(2)如图,当裁剪直线DE不平行于BC时;
那么,四边形DBCE的内角和也为360°吗?
问题2:已知△ABC ,如果沿直线剪去△ABC 中的∠A
一.问题:
问题3:根据问题1和问题2,我们能得出什么猜想?
猜想:任意一个四边形的内角和等于360°.
你能证明你的猜想吗?
一.问题:
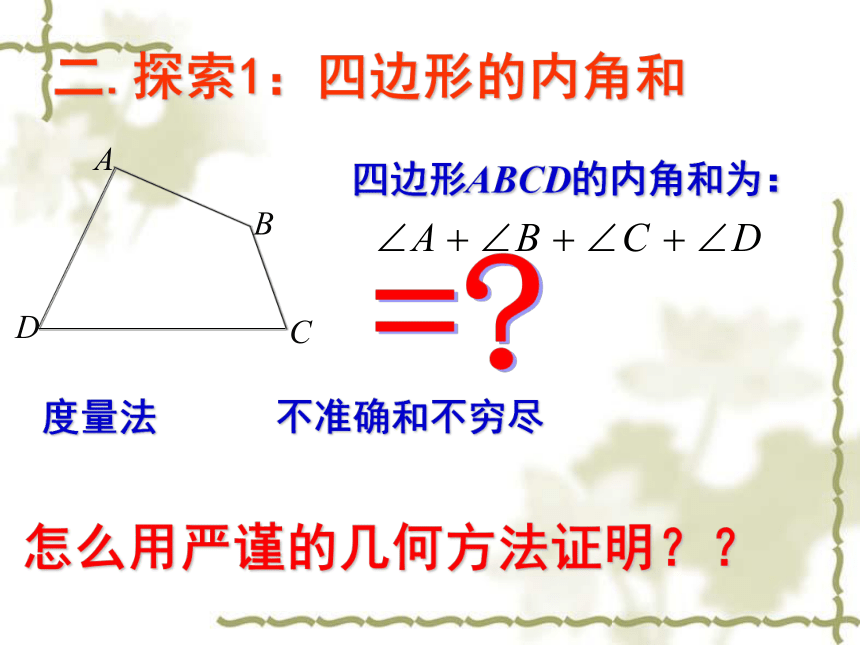
二.探索1:四边形的内角和
A
B
D
C
四边形ABCD的内角和为:
=
怎么用严谨的几何方法证明??
度量法
不准确和不穷尽
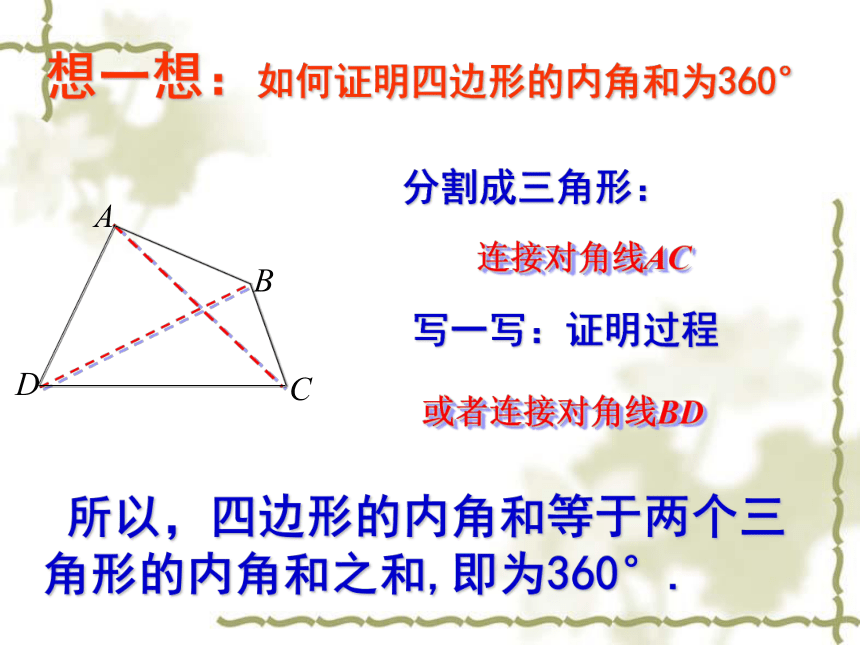
想一想:如何证明四边形的内角和为360°
连接对角线AC
或者连接对角线BD
所以,四边形的内角和等于两个三角形的内角和之和,即为360°.
A
B
D
C
分割成三角形:
写一写:证明过程
E
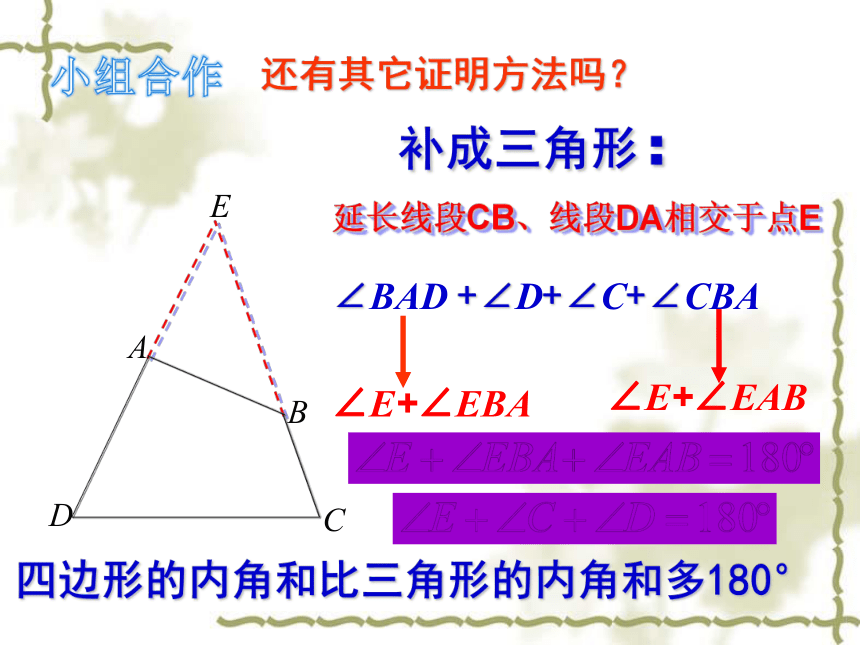
补成三角形:
延长线段CB、线段DA相交于点E
小组合作
还有其它证明方法吗?
A
B
D
C
∠BAD +∠D+∠C+∠CBA
∠E+∠EBA
∠E+∠EAB
四边形的内角和比三角形的内角和多180°
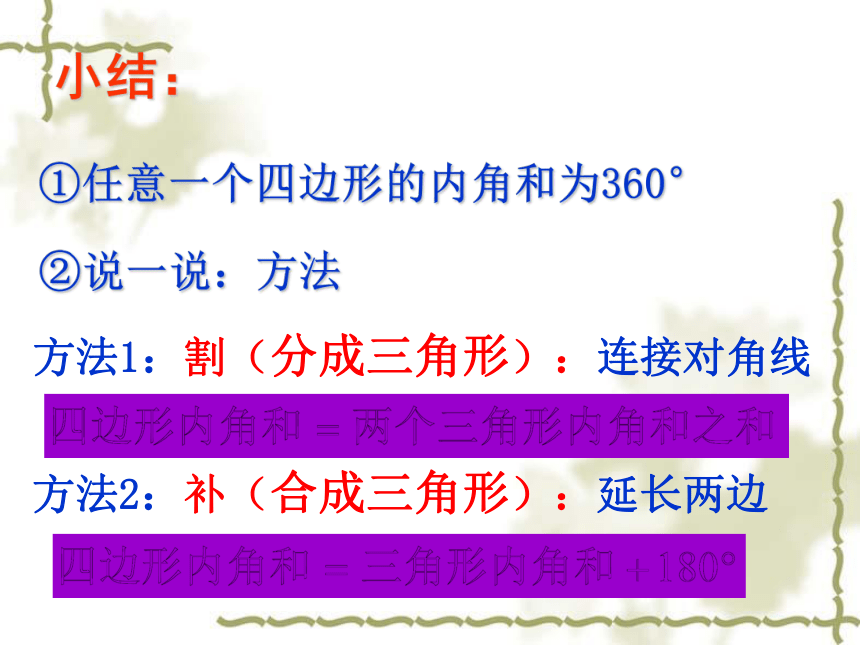
方法1:割(分成三角形):连接对角线
①任意一个四边形的内角和为360°
②说一说:方法
小结:
方法2:补(合成三角形):延长两边
二.探索2:求五边形的内角和
类比方法1:从五边形的一个顶点出发,可以作____条对角线,它们将五边形分为____个三角形,五边形的内角和等于_____×180°.
类比方法2:把五边形补成______,五边形的内角和比四边形的内角和多____
2
3
3
四边形
180°
二.探索2:求六边形的内角和
类比方法1:从六边形的一个顶点出发,可以作____条对角线,它们将六边形分为___个三角形,六边形的内角和等于_____×180°.
类比方法2:把六边形补成______,六边形的内角和比五边形的内角和多____
3
4
4
五边形
180°
三.探索3:n边形的内角和公式(割)
证明:从n 边形的一个顶点出发,可以作____条对角线,它们将n 边形分为____个三角形,n 边形的内角和等于_____×180°.
思考:你能从四边形、五边形、六边形的内角和的研究过程中发现多边形的内角和与边数n的关系?能证明你的结论吗?
n-3
n-2
(n-2)
n边形的内角和=(n-2)×180°
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 内角和的计算规律
三角形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2)×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
归纳:
小组交流讨论一下:还有其他分割方法吗?
我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
说一说:
如果当点在n边形的外部呢?
三.探索3:n边形的内角和公式(补)
多边形 内角和
三角形
四边形
五边形
六边形
n边形
…
…
结论:n边形的内角和=(n-2)×180°
180°
180°+180°=2×180°
180°+180°+180°=3×180°
180°+180°+180°+180°=4×180°
180°+180°+180°+…+180°=(n-2)×180°
四.例题讲解
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
已知:如图所示,四边形ABCD中∠A+∠C=180°.
求:∠B与∠D的关系
D
C
A
B
解:∵∠A+∠B+∠C+∠D
=(4-2)×180°
=360°,
∴∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
这就是说,如果四边形的一组对角互补,另一组对角也互补
十二边形的内角和是 .
一个多边形当边数增加1时,它的内角和增加 .
一个多边形的内角和是720°,则此多边形共有 ______个内角.
如果一个多边形的内角和是1440°,那么此多边形是 边形.
1800°
180°
六
十
练一练:
四.例题讲解
例2 如图,在五边形的每一个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
已知:如图所示,∠1,∠2,∠3,∠4,∠5, 分别为五边形ABCDE的外角.
求: ∠1+∠2+∠3+∠4+∠5的值
解:∵五边形的任何一个外角加上它相邻的内角和为180°
∴五边形的5个外角加上它们相邻的内角,得到总和等于5×180°
∵五边形的内角和为(5-2)×180°=540°
∴五边形的外角和为5×180°- 540°=360°
E
B
C
D
1
2
3
4
5
A
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
n边形的外角和等于360°,且与多边形的边长无关
-(n-2) × 180°
=360°.
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180°
五.探索4:n边形的外角和公式
多边形的外角和等于360°,能否运用其他方法进行验证?
验证:n边形的外角和为360°
A
如图,从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.
此时,多边形的外角和是什么?
在行程中所转的各个角的和
由于走了一周,所转的各个角的和等于一个周角,
所以多边形的外角和等于360°
六.小结反思
三.通过本节课学习,你学习到的数学思想方 法有哪些?你还有什么疑惑
(1)多边形的内角和公式为(n-2)×180°
(2)多边形的外角和等于360°
一.本节课我们学习了哪些主要内容?
二.我们是如何得到多边形的内角和公式的?
七.作业
1. 必做题:
2. 选做题:
(1)小明在计算某个多边形的内角和时,由于 粗心他漏掉一个内角,求得的内角和1680°,你能否求得正确结果呢?
(2)一天小明爸爸给小明出了一道智力题考考他。将一个多 边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定
谢谢!
青岛2011课标版 《数学》七年级下册
13.2.2多边形的内角和与外角和
一.问题:
问题1:我们学过哪些几何图形的内角和?
三角形内角和为180°
正方形内角和为360°
那么,任意一个四边形的内角和等于360°?
长方形内角和为360°
问题2:已知△ABC ,如果沿直线剪去△ABC 中的∠A
A
B
C
A
B
C
D
E
B
C
D
E
(1)如图,当裁剪直线DE平行于BC时;
根据平行线的性质,四边形DBCE的内角和为360°
一.问题:
想一想:四边形DBCE的内角和为多少?
A
B
C
A
B
C
D
E
B
C
D
E
(2)如图,当裁剪直线DE不平行于BC时;
那么,四边形DBCE的内角和也为360°吗?
问题2:已知△ABC ,如果沿直线剪去△ABC 中的∠A
一.问题:
问题3:根据问题1和问题2,我们能得出什么猜想?
猜想:任意一个四边形的内角和等于360°.
你能证明你的猜想吗?
一.问题:
二.探索1:四边形的内角和
A
B
D
C
四边形ABCD的内角和为:
=
怎么用严谨的几何方法证明??
度量法
不准确和不穷尽
想一想:如何证明四边形的内角和为360°
连接对角线AC
或者连接对角线BD
所以,四边形的内角和等于两个三角形的内角和之和,即为360°.
A
B
D
C
分割成三角形:
写一写:证明过程
E
补成三角形:
延长线段CB、线段DA相交于点E
小组合作
还有其它证明方法吗?
A
B
D
C
∠BAD +∠D+∠C+∠CBA
∠E+∠EBA
∠E+∠EAB
四边形的内角和比三角形的内角和多180°
方法1:割(分成三角形):连接对角线
①任意一个四边形的内角和为360°
②说一说:方法
小结:
方法2:补(合成三角形):延长两边
二.探索2:求五边形的内角和
类比方法1:从五边形的一个顶点出发,可以作____条对角线,它们将五边形分为____个三角形,五边形的内角和等于_____×180°.
类比方法2:把五边形补成______,五边形的内角和比四边形的内角和多____
2
3
3
四边形
180°
二.探索2:求六边形的内角和
类比方法1:从六边形的一个顶点出发,可以作____条对角线,它们将六边形分为___个三角形,六边形的内角和等于_____×180°.
类比方法2:把六边形补成______,六边形的内角和比五边形的内角和多____
3
4
4
五边形
180°
三.探索3:n边形的内角和公式(割)
证明:从n 边形的一个顶点出发,可以作____条对角线,它们将n 边形分为____个三角形,n 边形的内角和等于_____×180°.
思考:你能从四边形、五边形、六边形的内角和的研究过程中发现多边形的内角和与边数n的关系?能证明你的结论吗?
n-3
n-2
(n-2)
n边形的内角和=(n-2)×180°
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 内角和的计算规律
三角形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2)×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
归纳:
小组交流讨论一下:还有其他分割方法吗?
我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
说一说:
如果当点在n边形的外部呢?
三.探索3:n边形的内角和公式(补)
多边形 内角和
三角形
四边形
五边形
六边形
n边形
…
…
结论:n边形的内角和=(n-2)×180°
180°
180°+180°=2×180°
180°+180°+180°=3×180°
180°+180°+180°+180°=4×180°
180°+180°+180°+…+180°=(n-2)×180°
四.例题讲解
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
已知:如图所示,四边形ABCD中∠A+∠C=180°.
求:∠B与∠D的关系
D
C
A
B
解:∵∠A+∠B+∠C+∠D
=(4-2)×180°
=360°,
∴∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
这就是说,如果四边形的一组对角互补,另一组对角也互补
十二边形的内角和是 .
一个多边形当边数增加1时,它的内角和增加 .
一个多边形的内角和是720°,则此多边形共有 ______个内角.
如果一个多边形的内角和是1440°,那么此多边形是 边形.
1800°
180°
六
十
练一练:
四.例题讲解
例2 如图,在五边形的每一个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
已知:如图所示,∠1,∠2,∠3,∠4,∠5, 分别为五边形ABCDE的外角.
求: ∠1+∠2+∠3+∠4+∠5的值
解:∵五边形的任何一个外角加上它相邻的内角和为180°
∴五边形的5个外角加上它们相邻的内角,得到总和等于5×180°
∵五边形的内角和为(5-2)×180°=540°
∴五边形的外角和为5×180°- 540°=360°
E
B
C
D
1
2
3
4
5
A
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
n边形的外角和等于360°,且与多边形的边长无关
-(n-2) × 180°
=360°.
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180°
五.探索4:n边形的外角和公式
多边形的外角和等于360°,能否运用其他方法进行验证?
验证:n边形的外角和为360°
A
如图,从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.
此时,多边形的外角和是什么?
在行程中所转的各个角的和
由于走了一周,所转的各个角的和等于一个周角,
所以多边形的外角和等于360°
六.小结反思
三.通过本节课学习,你学习到的数学思想方 法有哪些?你还有什么疑惑
(1)多边形的内角和公式为(n-2)×180°
(2)多边形的外角和等于360°
一.本节课我们学习了哪些主要内容?
二.我们是如何得到多边形的内角和公式的?
七.作业
1. 必做题:
2. 选做题:
(1)小明在计算某个多边形的内角和时,由于 粗心他漏掉一个内角,求得的内角和1680°,你能否求得正确结果呢?
(2)一天小明爸爸给小明出了一道智力题考考他。将一个多 边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定
谢谢!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
