青岛版七下数学12.2 完全平方公式 课件(23张PPT)
文档属性
| 名称 | 青岛版七下数学12.2 完全平方公式 课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 861.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 06:47:07 | ||
图片预览



文档简介
(共23张PPT)
青岛2011课标版七年级下册第十二章第二节
《完全平方公式》
巴依老爷逼着我用他的一
块地换我 的两块地,我该不该
跟他换呢?会吃亏吗?
创设情境 点燃学生兴奋点
阿凡提的两块地
肯定比我的一块地多,我必须把它换过来!
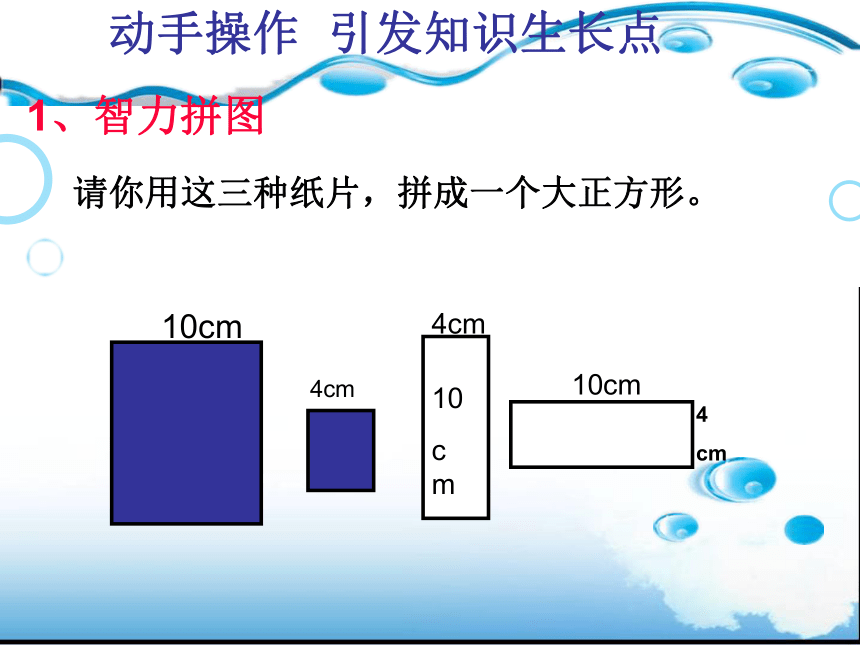
1、智力拼图
10cm
4cm
10
cm
4cm
4
cm
10cm
动手操作 引发知识生长点
请你用这三种纸片,拼成一个大正方形。
4cm
10
cm
4cm
10cm
10cm
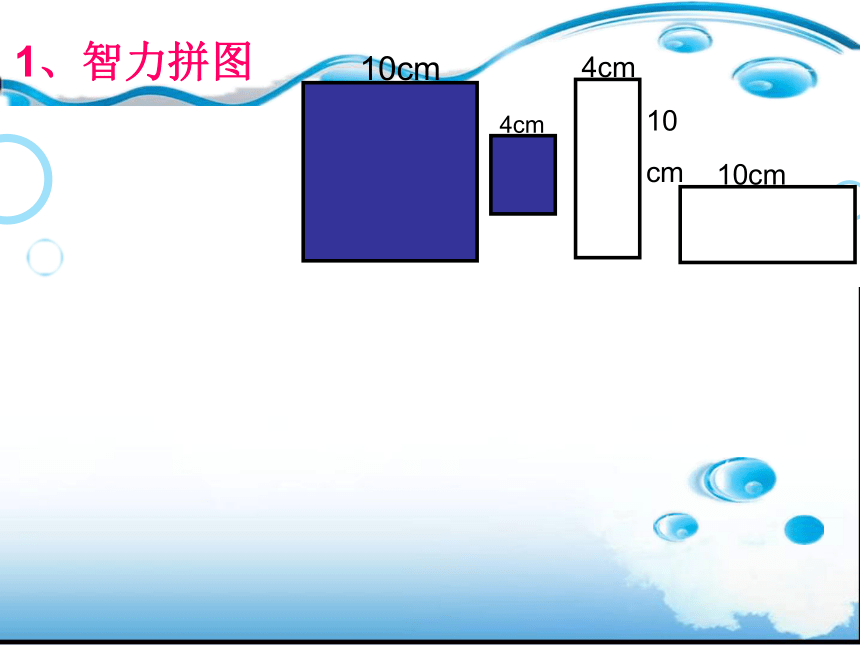
1、智力拼图
4cm
10
cm
4cm
10cm
10cm
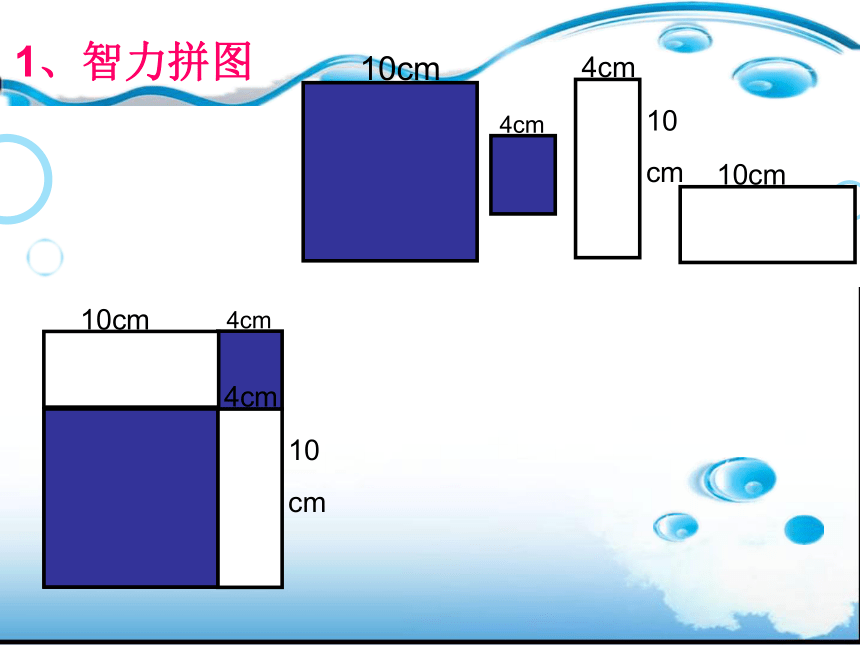
1、智力拼图
5cm
4cm
10
cm
4cm
10cm
10cm
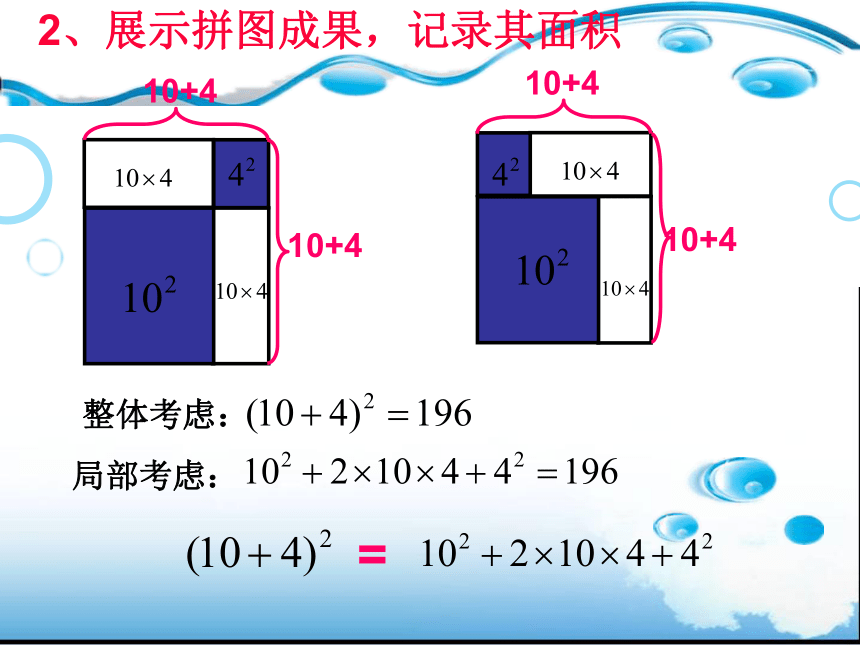
2、展示拼图成果,记录其面积
10+4
10+4
10+4
10+4
整体考虑:
局部考虑:
=
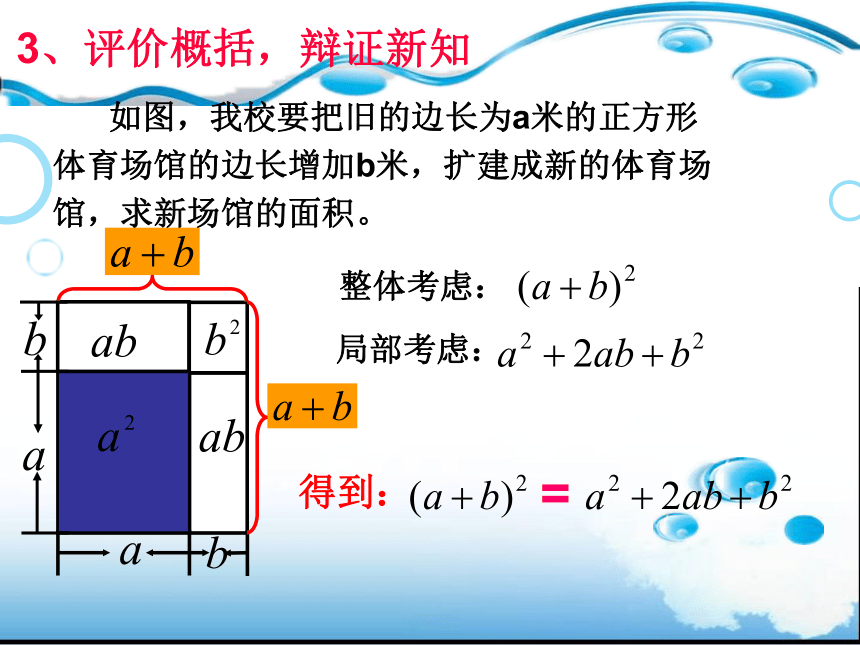
如图,我校要把旧的边长为a米的正方形
体育场馆的边长增加b米,扩建成新的体育场
馆,求新场馆的面积。
3、评价概括,辩证新知
整体考虑:
局部考虑:
得到:
=
用多项式乘法法则验证:
请你观察公式,总结公式的结构特点。
4、观察公式,辨明真身
完全平方公式的语言表述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
两倍乘积放中央,
同加异减看前方.
完全平方公式的语言表述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
简单记为:
首平方,
尾平方,
Ⅱ、平方差公式与完全平方公式进行比较,二者有何区别?
完全平方公式
平方差公式
5、解决疑问,突出重点
智力拼图:
(1)用纸片分别拼出面积为 和
的图形。
≠
5、解决疑问,突出重点
智力拼图:
(2)用纸片分别拼出面积为 和 的图形。
≠
(一)趁热打铁,小试身手
1、判断:下列式子中可以选用完全平方公式进行计算有:
学以致用,训练思维发散点
2、填空:
(二)范例解析,巩固新知
例1 运用完全平方公式计算:
例题2 运用完全平方公式计算:
(1) ;
(2) ;
(三)拓广探索,提升能力
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形。
图(2)
图(1)
2a
2b
(1)图(2)中阴影部分的正方形的边长是_______;
(2)请用两种不同的方法求图(2)中阴影部分的面积:
方法一:__________________________;
方法二:__________________________。
(3)观察图(2),你能写出下列三个代数式之间的等量关系吗?
代数式: 、 、
等量关系:_______________________。
(4)根据第(3)题中的等量关系解决如下问题:
若 , ,
则 =_____________。
图(2)
图(1)
2a
2b
28
必做题:
1、运用完全平方公式计算(课本P112第2题)。
布置作业 延伸新知
(1)
(2)
(3)
(4)
(5)
(6)
必做题:
2、如图所示,下列四种图形中,图1是长方形,图2、3、4
是正方形,把图1、2、3不重叠、无缝隙地拼在一起,则其
面积 =_______;图4的面积 =______;
则 _____ (填“>”、“<”或“=”)。
图1
图2
图3
图4
布置作业 延伸新知
选做题:
1、计算:
2、选择题:
有3张边长为a的正方形纸片,4张边长分别为a、b(b>a)的矩形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
B. C. D.
这节课我学会了...
青岛2011课标版七年级下册第十二章第二节
《完全平方公式》
巴依老爷逼着我用他的一
块地换我 的两块地,我该不该
跟他换呢?会吃亏吗?
创设情境 点燃学生兴奋点
阿凡提的两块地
肯定比我的一块地多,我必须把它换过来!
1、智力拼图
10cm
4cm
10
cm
4cm
4
cm
10cm
动手操作 引发知识生长点
请你用这三种纸片,拼成一个大正方形。
4cm
10
cm
4cm
10cm
10cm
1、智力拼图
4cm
10
cm
4cm
10cm
10cm
1、智力拼图
5cm
4cm
10
cm
4cm
10cm
10cm
2、展示拼图成果,记录其面积
10+4
10+4
10+4
10+4
整体考虑:
局部考虑:
=
如图,我校要把旧的边长为a米的正方形
体育场馆的边长增加b米,扩建成新的体育场
馆,求新场馆的面积。
3、评价概括,辩证新知
整体考虑:
局部考虑:
得到:
=
用多项式乘法法则验证:
请你观察公式,总结公式的结构特点。
4、观察公式,辨明真身
完全平方公式的语言表述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
两倍乘积放中央,
同加异减看前方.
完全平方公式的语言表述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
简单记为:
首平方,
尾平方,
Ⅱ、平方差公式与完全平方公式进行比较,二者有何区别?
完全平方公式
平方差公式
5、解决疑问,突出重点
智力拼图:
(1)用纸片分别拼出面积为 和
的图形。
≠
5、解决疑问,突出重点
智力拼图:
(2)用纸片分别拼出面积为 和 的图形。
≠
(一)趁热打铁,小试身手
1、判断:下列式子中可以选用完全平方公式进行计算有:
学以致用,训练思维发散点
2、填空:
(二)范例解析,巩固新知
例1 运用完全平方公式计算:
例题2 运用完全平方公式计算:
(1) ;
(2) ;
(三)拓广探索,提升能力
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形。
图(2)
图(1)
2a
2b
(1)图(2)中阴影部分的正方形的边长是_______;
(2)请用两种不同的方法求图(2)中阴影部分的面积:
方法一:__________________________;
方法二:__________________________。
(3)观察图(2),你能写出下列三个代数式之间的等量关系吗?
代数式: 、 、
等量关系:_______________________。
(4)根据第(3)题中的等量关系解决如下问题:
若 , ,
则 =_____________。
图(2)
图(1)
2a
2b
28
必做题:
1、运用完全平方公式计算(课本P112第2题)。
布置作业 延伸新知
(1)
(2)
(3)
(4)
(5)
(6)
必做题:
2、如图所示,下列四种图形中,图1是长方形,图2、3、4
是正方形,把图1、2、3不重叠、无缝隙地拼在一起,则其
面积 =_______;图4的面积 =______;
则 _____ (填“>”、“<”或“=”)。
图1
图2
图3
图4
布置作业 延伸新知
选做题:
1、计算:
2、选择题:
有3张边长为a的正方形纸片,4张边长分别为a、b(b>a)的矩形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
B. C. D.
这节课我学会了...
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
