2022版新教材高中数学第一章空间向量与立体几何1.2空间向量基本定理课件新人教A版选择性必修第一册(57张ppt)
文档属性
| 名称 | 2022版新教材高中数学第一章空间向量与立体几何1.2空间向量基本定理课件新人教A版选择性必修第一册(57张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 07:46:08 | ||
图片预览











文档简介
(共57张PPT)
第一章 空间向量与立体几何
1.2 空间向量基本定理
课 标 解 读 课标要求 素养要求
1.了解空间向量基本定理及其意义. 2.掌握空间向量的正交分解及其坐标表示. 3.能用空间向量基本定理解决有关问题. 1.逻辑推理一能运用空间向量基本定理解决空间中平行与垂直的证明问题.
2.数学运算一能运 用基底思想和向量运算解决立体几何中的问题.
要点一 空间向量基本定律
空间向量基本定理:
(1)定理:如果三个向量,,不共面,那么对任意一个空间向量,存在唯一的有序实数组,使得.
(2)基底:如果三个向量,,①_______,那么所有空间向量组成的集合就是.这个集合可看作由向量,,生成的,我们把叫做空间的个②_____,,,都叫做基向量.
不共面
基底
要点二 空间向量的正交分解
空间向量的正交分解及其坐标表示:
(1)单位正交基底:如果空间的一-个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做③_____________,常用表示.
(2)正交分解:把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行④_________.
单位正交基底
正交分解
1.基底选定后,空间中的所有向量均可由该基底唯一表示吗?不同基底下,同一个向量的表达式都相同吗?
提示 基底选定后,空间中的所有向量均可由该基底唯一表示,不一定相同,不同基底下,同一个向量的表达式也有可能不同.
2.在“"中能否有零向量?
提示 不能,因为0与任意一个非零向量共线,与任意两个非零向量共面.
3.当给定的三个向量两两垂直时,请用图形验证任意给定的空间向量是否可以用给定的三个向量线性表示.
提示
1.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.基底的选择一般有两个条件:(1)基底必须是不共面的非零向量;(2)在进行基底选择时要尽量选择已知夹角和长度的向量,这样会让后续计算比较方便.
2.因为零向量与任意一个非零向量共线,与任意两个不共线的向量共面,所以如果三个向量不共面,就说明它们都不是零向量.
探究点一 基底的判断
例 (多选题)设,且是空间的一个基底,则下列可以作为空间的一个基底的有( )
A. B.
C. D.
BCD
思路分析只要所给的三个向量不共面,即可作为空间的一个基底,故逐一判断四组向量是否共面即可.
[解析]不可以,
,
共面,
不可以作为空间的一个基底;
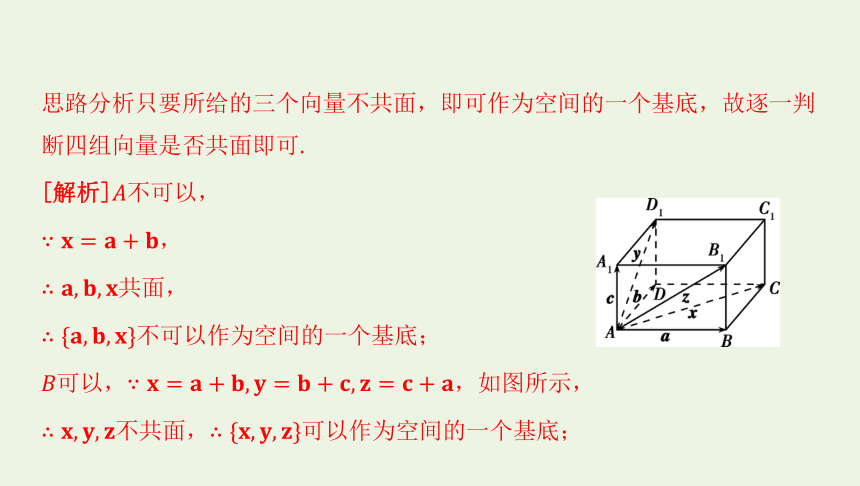
可以,,如图所示,
不共面,可以作为空间的一个基底;
可以,不共面,可以作为空间的一个基底;
可以,假设共面,则存在实数,使得,
此方程组无解,不存在实数使得共面,
可以作为空间的一个基底.
综上,B、C、D满足题意.
解题感悟
判断基底的基本思路:①若向量中存在零向量,则不能作为基底;若存在一个向量可以用另外的向量线性表示,则不能构成基底;②假设,运用空间向量基本定理,联立的方程,若有解,则共面,不能作为基底;若无解,则不共面,能作为基底.
已知是空间的一个基底,且,试判断能否作为空间的一个基底.
[答案] 假设共面,则由向量共面的充要条件可知,存在实数,使得,
,
即,
此方程组无解,即不存在实数,使得
不共面,能作为空间的一个基底.
探究点二 用基底表示向量
类型1 用基底表示向量
例1 如图,四棱锥的底面是矩形,平面,设分别是的中点,试用表示.
连接(图略),则,,
,
,
.
解题感悟
用基底表示一个向量时,如果此向量的起点是从基底的公共点出发的,一般用加法运算,否则用减法运算;如果此向量与一个易求的向量共线,可用数乘运算.
类型2 单位正交基底的应用
例2 (原创题)正方体的棱长为与的交点为与的交点为.
(1) 求证:;
[答案] 证明:设,则构成空间的一个单位正交基底,如图,
,
,所以,所以.
(2) 求的值.
[答案] 由(1)可知,
所以
,所以.
解题感悟
单位正交基底的特点是两两垂直,模为1,它的应用可类比基底的应用.
1. [2021北京平谷五中高二月考] 在四面体中,为的中点,为上一点,且,设,则
( )
A. B.
C. D.
D
[解析] 根据题意得,,
,
又.
2. (原创题)如图所示,在棱长为1的正方体中,设,分别是正方形和的中心.
[答案] 设,则构成空间的一个单位正交基底,
所以,
,
所以,所以,
故异面直线与所成的角为.
(1) 求异面直线与所成的角;
(2) 求的长.
[答案] ,
所以,
所以,
故的长为.
探究点三 空间向量的综合应用
例 如图,已知空间四边形的各边及对角线长都为2,是的中点,在线段上,且.
[答案] 因为是的中点,在线段上,且,
所以,
所以.
(1) 用表示;
[答案] 由(1)可得,
所以
,
(2) 求向量与向量所成角的余弦值.
,
因为,
所以向量与向量所成角的余弦值为.
解题感悟
解决空间向量的模、夹角及证明垂直的问题时,常常先将所求向量用某个基底表示,再根据空间向量的线性运算求解.
已知在空间四边形中,,且分别是的中点,是的中点,求证:.
[答案] 证明:如图所示,
设则,
,易知,
,即.
1. 已知是空间的一个单位正交基底,且,则与夹角的余弦值为( )
A. B. C. D.
D
2. 在长方体中,可以作为空间的一个基底的是
( )
A. B.
C. D.
C
3. (改编题)若是空间的一个基底,则下列各组中不能构成空间的一个基底的是( )
A. B.
C. D.
C
4. 在空间四边形中,,点在线段上,且,点是的中点,则______________________.
[解析] 由题意得,
所以
.
1. [2021山东泰安高二期末] 已知空间四边形中,取基向量,点在线段上,且为的中点,则等于( )
A. B.
C. D.
B
[解析] 因为为的中点,
所以,
因为,所以,
所以.
2. (原创题)在长方体中,是侧面的中心,则异面直线与所成角的余弦值为( )
A. B. C. D.
D
3. [2020陕西商洛商丹高新学校高二期末] 在四面体中,分别是的中点,是的三等分点(靠近点),若,则( )
A. B.
C. D.
B
4. [2021山东淄博高二期末] (多选题)已知空间向量都是单位向量,且两两垂直,则下列结论正确的有( )
A. 向量的模是3
B. 可以构成空间的一个基底
C. 向量和夹角的余弦值为
D. 向量与共线
BC
[解析] ,故A中结论错误;
空间向量都是单位向量,且两两垂直,
均为非零向量,
,
两两垂直,则可以构成空间的一个基底,故B中结论正确;
,故C中结论正确;
,
,同理可得,
,
,故D中结论错误.
5. [2021河南平顶山高二期末] 在棱长为1的正四面体中,点分别是线段上的点,且满足,则
( )
A. B. C. D.
A
6. (多选题)(原创题)如图,正方体的棱长为1,点是上底面的中心,点是下底面的中心,是的中点,则下列结论正确的有( )
A. B. C. D.
AD
7. (多选题)已知是空间中的五点,且任意三点均不共线.若与均不能构成空间的一个基底,则下列结论中正确的有( )
A. 不能构成空间的一个基底
B. 能构成空间的一个基底
C. 不能构成空间的一个基底
D. 能构成空间的一个基底
AC
8. 如图,在四棱锥中,四边形为平行四边形,与交于点,点为上一点,用表示向量_____________________.
9. [2021辽宁大连瓦房店中学高二月考] (多选题)如图,在平行六面体中,以顶点为端点的三条棱长都相等,且它们彼此的夹角都是,则下列说法中正确的有( )
向量 与 的夹角是
与 所成角的余弦值为
AB
[解析] 因为以顶点为端点的三条棱长都相等,且它们彼此的夹角都是,所以可设该棱长为1,则,
易知,
且
易知,所以B中说法正确;
易知为等边三角形,所以,故向量与的夹角是,所以向量与的夹角是所以C中说法不正确;
易知,
所以,
所以,所以D中说法不正确.故选AB.
10. [2021北京平谷第五中学高二月考] 在正三棱柱中,,为棱的中点,则异面直线与所成角的大小为__________.
[解析] 如图,
取空间的一个基底,
则,
该三棱柱的侧棱和底面垂直,
,
又,
,
,
异面直线与所成角的大小为.
11. 已知为空间的一个基底,若,则分别为_________________.
[解析] 由题意得a、b、c为三个不共面的向量,由空间向量基本定理可知必然存在唯一的有序实数组,使得成立,
.
,
12. 如图,在正方体中,分别是棱的中点,求证:平面.
[解析] 命题分析 本题主要考查了线面垂直的判定定理,向量数量积的运算,向量垂直的应用.
答题要领 设,则构成空间的一个基底,利用向量的数量积等于零,把用单位正交基底表示,由向量数量积的运算以及线面垂直的判定定理,即可证出平面.
解题感悟
在用线面垂直的判定定理证明时,必须说明两条直线相交.证明线面垂直时,可先利用向量数量积的运算证明线线垂直.
[答案] 证明 设则为空间的一个基底,
,
,同理可得,
又平面,
平面.
第一章 空间向量与立体几何
1.2 空间向量基本定理
课 标 解 读 课标要求 素养要求
1.了解空间向量基本定理及其意义. 2.掌握空间向量的正交分解及其坐标表示. 3.能用空间向量基本定理解决有关问题. 1.逻辑推理一能运用空间向量基本定理解决空间中平行与垂直的证明问题.
2.数学运算一能运 用基底思想和向量运算解决立体几何中的问题.
要点一 空间向量基本定律
空间向量基本定理:
(1)定理:如果三个向量,,不共面,那么对任意一个空间向量,存在唯一的有序实数组,使得.
(2)基底:如果三个向量,,①_______,那么所有空间向量组成的集合就是.这个集合可看作由向量,,生成的,我们把叫做空间的个②_____,,,都叫做基向量.
不共面
基底
要点二 空间向量的正交分解
空间向量的正交分解及其坐标表示:
(1)单位正交基底:如果空间的一-个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做③_____________,常用表示.
(2)正交分解:把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行④_________.
单位正交基底
正交分解
1.基底选定后,空间中的所有向量均可由该基底唯一表示吗?不同基底下,同一个向量的表达式都相同吗?
提示 基底选定后,空间中的所有向量均可由该基底唯一表示,不一定相同,不同基底下,同一个向量的表达式也有可能不同.
2.在“"中能否有零向量?
提示 不能,因为0与任意一个非零向量共线,与任意两个非零向量共面.
3.当给定的三个向量两两垂直时,请用图形验证任意给定的空间向量是否可以用给定的三个向量线性表示.
提示
1.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.基底的选择一般有两个条件:(1)基底必须是不共面的非零向量;(2)在进行基底选择时要尽量选择已知夹角和长度的向量,这样会让后续计算比较方便.
2.因为零向量与任意一个非零向量共线,与任意两个不共线的向量共面,所以如果三个向量不共面,就说明它们都不是零向量.
探究点一 基底的判断
例 (多选题)设,且是空间的一个基底,则下列可以作为空间的一个基底的有( )
A. B.
C. D.
BCD
思路分析只要所给的三个向量不共面,即可作为空间的一个基底,故逐一判断四组向量是否共面即可.
[解析]不可以,
,
共面,
不可以作为空间的一个基底;
可以,,如图所示,
不共面,可以作为空间的一个基底;
可以,不共面,可以作为空间的一个基底;
可以,假设共面,则存在实数,使得,
此方程组无解,不存在实数使得共面,
可以作为空间的一个基底.
综上,B、C、D满足题意.
解题感悟
判断基底的基本思路:①若向量中存在零向量,则不能作为基底;若存在一个向量可以用另外的向量线性表示,则不能构成基底;②假设,运用空间向量基本定理,联立的方程,若有解,则共面,不能作为基底;若无解,则不共面,能作为基底.
已知是空间的一个基底,且,试判断能否作为空间的一个基底.
[答案] 假设共面,则由向量共面的充要条件可知,存在实数,使得,
,
即,
此方程组无解,即不存在实数,使得
不共面,能作为空间的一个基底.
探究点二 用基底表示向量
类型1 用基底表示向量
例1 如图,四棱锥的底面是矩形,平面,设分别是的中点,试用表示.
连接(图略),则,,
,
,
.
解题感悟
用基底表示一个向量时,如果此向量的起点是从基底的公共点出发的,一般用加法运算,否则用减法运算;如果此向量与一个易求的向量共线,可用数乘运算.
类型2 单位正交基底的应用
例2 (原创题)正方体的棱长为与的交点为与的交点为.
(1) 求证:;
[答案] 证明:设,则构成空间的一个单位正交基底,如图,
,
,所以,所以.
(2) 求的值.
[答案] 由(1)可知,
所以
,所以.
解题感悟
单位正交基底的特点是两两垂直,模为1,它的应用可类比基底的应用.
1. [2021北京平谷五中高二月考] 在四面体中,为的中点,为上一点,且,设,则
( )
A. B.
C. D.
D
[解析] 根据题意得,,
,
又.
2. (原创题)如图所示,在棱长为1的正方体中,设,分别是正方形和的中心.
[答案] 设,则构成空间的一个单位正交基底,
所以,
,
所以,所以,
故异面直线与所成的角为.
(1) 求异面直线与所成的角;
(2) 求的长.
[答案] ,
所以,
所以,
故的长为.
探究点三 空间向量的综合应用
例 如图,已知空间四边形的各边及对角线长都为2,是的中点,在线段上,且.
[答案] 因为是的中点,在线段上,且,
所以,
所以.
(1) 用表示;
[答案] 由(1)可得,
所以
,
(2) 求向量与向量所成角的余弦值.
,
因为,
所以向量与向量所成角的余弦值为.
解题感悟
解决空间向量的模、夹角及证明垂直的问题时,常常先将所求向量用某个基底表示,再根据空间向量的线性运算求解.
已知在空间四边形中,,且分别是的中点,是的中点,求证:.
[答案] 证明:如图所示,
设则,
,易知,
,即.
1. 已知是空间的一个单位正交基底,且,则与夹角的余弦值为( )
A. B. C. D.
D
2. 在长方体中,可以作为空间的一个基底的是
( )
A. B.
C. D.
C
3. (改编题)若是空间的一个基底,则下列各组中不能构成空间的一个基底的是( )
A. B.
C. D.
C
4. 在空间四边形中,,点在线段上,且,点是的中点,则______________________.
[解析] 由题意得,
所以
.
1. [2021山东泰安高二期末] 已知空间四边形中,取基向量,点在线段上,且为的中点,则等于( )
A. B.
C. D.
B
[解析] 因为为的中点,
所以,
因为,所以,
所以.
2. (原创题)在长方体中,是侧面的中心,则异面直线与所成角的余弦值为( )
A. B. C. D.
D
3. [2020陕西商洛商丹高新学校高二期末] 在四面体中,分别是的中点,是的三等分点(靠近点),若,则( )
A. B.
C. D.
B
4. [2021山东淄博高二期末] (多选题)已知空间向量都是单位向量,且两两垂直,则下列结论正确的有( )
A. 向量的模是3
B. 可以构成空间的一个基底
C. 向量和夹角的余弦值为
D. 向量与共线
BC
[解析] ,故A中结论错误;
空间向量都是单位向量,且两两垂直,
均为非零向量,
,
两两垂直,则可以构成空间的一个基底,故B中结论正确;
,故C中结论正确;
,
,同理可得,
,
,故D中结论错误.
5. [2021河南平顶山高二期末] 在棱长为1的正四面体中,点分别是线段上的点,且满足,则
( )
A. B. C. D.
A
6. (多选题)(原创题)如图,正方体的棱长为1,点是上底面的中心,点是下底面的中心,是的中点,则下列结论正确的有( )
A. B. C. D.
AD
7. (多选题)已知是空间中的五点,且任意三点均不共线.若与均不能构成空间的一个基底,则下列结论中正确的有( )
A. 不能构成空间的一个基底
B. 能构成空间的一个基底
C. 不能构成空间的一个基底
D. 能构成空间的一个基底
AC
8. 如图,在四棱锥中,四边形为平行四边形,与交于点,点为上一点,用表示向量_____________________.
9. [2021辽宁大连瓦房店中学高二月考] (多选题)如图,在平行六面体中,以顶点为端点的三条棱长都相等,且它们彼此的夹角都是,则下列说法中正确的有( )
向量 与 的夹角是
与 所成角的余弦值为
AB
[解析] 因为以顶点为端点的三条棱长都相等,且它们彼此的夹角都是,所以可设该棱长为1,则,
易知,
且
易知,所以B中说法正确;
易知为等边三角形,所以,故向量与的夹角是,所以向量与的夹角是所以C中说法不正确;
易知,
所以,
所以,所以D中说法不正确.故选AB.
10. [2021北京平谷第五中学高二月考] 在正三棱柱中,,为棱的中点,则异面直线与所成角的大小为__________.
[解析] 如图,
取空间的一个基底,
则,
该三棱柱的侧棱和底面垂直,
,
又,
,
,
异面直线与所成角的大小为.
11. 已知为空间的一个基底,若,则分别为_________________.
[解析] 由题意得a、b、c为三个不共面的向量,由空间向量基本定理可知必然存在唯一的有序实数组,使得成立,
.
,
12. 如图,在正方体中,分别是棱的中点,求证:平面.
[解析] 命题分析 本题主要考查了线面垂直的判定定理,向量数量积的运算,向量垂直的应用.
答题要领 设,则构成空间的一个基底,利用向量的数量积等于零,把用单位正交基底表示,由向量数量积的运算以及线面垂直的判定定理,即可证出平面.
解题感悟
在用线面垂直的判定定理证明时,必须说明两条直线相交.证明线面垂直时,可先利用向量数量积的运算证明线线垂直.
[答案] 证明 设则为空间的一个基底,
,
,同理可得,
又平面,
平面.
