2022版新教材高中数学第一章空间向量与立体几何章末总结课件新人教A版选择性必修第一册(78张ppt)
文档属性
| 名称 | 2022版新教材高中数学第一章空间向量与立体几何章末总结课件新人教A版选择性必修第一册(78张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 07:55:42 | ||
图片预览

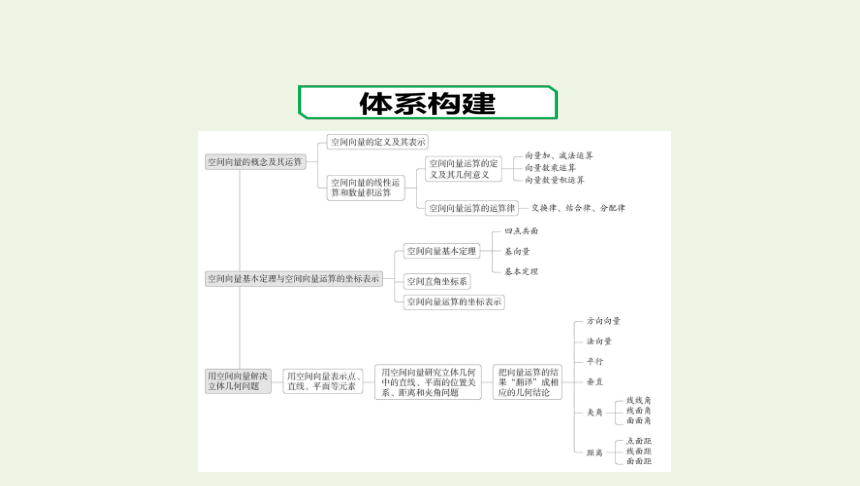








文档简介
(共78张PPT)
第一章 空间向量与立体几何
章末总结
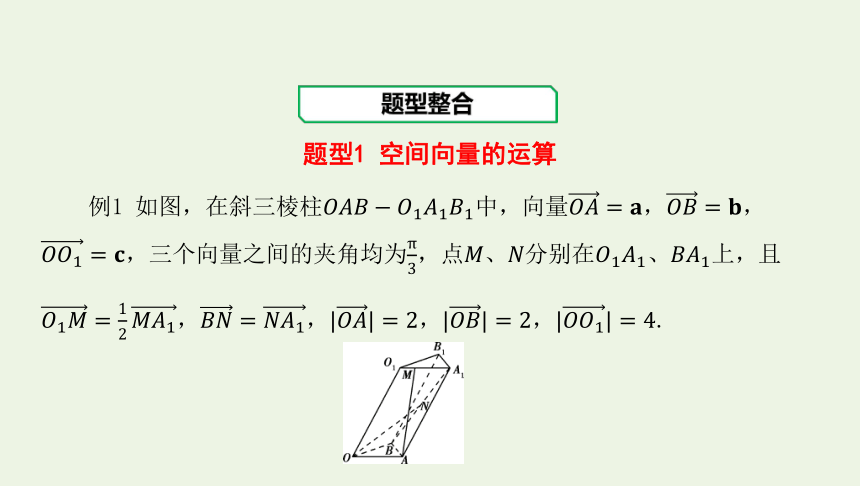
题型1 空间向量的运算
例1 如图,在斜三棱柱中,向量,,,三个向量之间的夹角均为,点分别在上,且,,,,.
(1) 将向量用向量表示,并求;
[答案] ,
因为,
所以,
所以.
(2) 将向量用表示.
[答案] 因为,所以为的中点,
所以.
方法归纳
在几何体中,根据图形的特点,选择公共起点最集中的向量中的三个不共面的向量作为基底或选择有公共起点且关系最明确(如夹角或线段的长度)的三个不共面的向量作为基底,这样更利于解题.
1. 如图,在四棱锥中,底面是边长为1的正方形,到的距离都等于2.给出以下结论:①;②;③;④,其中正确结论的序号是_________ .
②③
[解析] 易知,所以②中结论正确;因为底面ABCD是边长为1的正方形,,所以,,又,所以,所以③中结论正确;显然①、④中结论不正确.故正确结论的序号是②③.
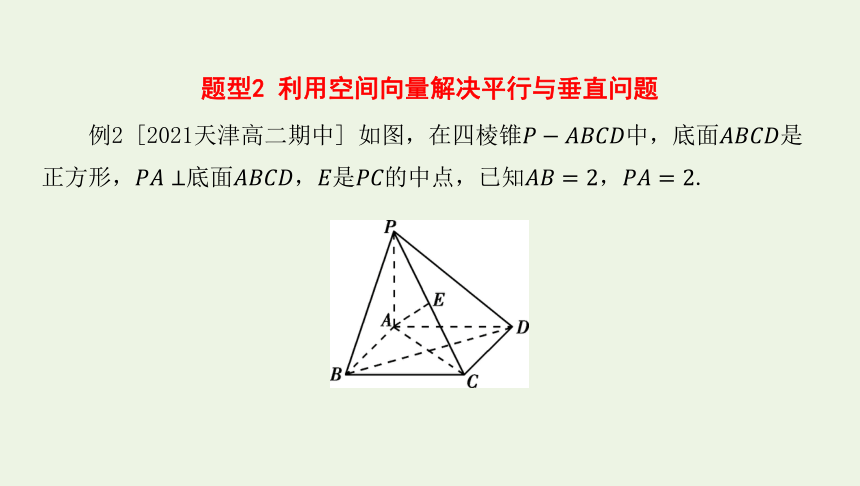
题型2 利用空间向量解决平行与垂直问题
例2 [2021天津高二期中] 如图,在四棱锥中,底面是正方形,底面,是的中点,已知,.
[答案] 因为是的中点,所以的坐标为(1,1,1),
所以,
易知,所以,
所以,即.
(1) 求证:;
[答案] 因为底面是正方形,所以,
因为底面,底面,
所以,因为,,平面,所以平面,
所以平面的一个法向量为,
设平面的法向量为,易知,
(2) 求证:平面平面.
则取,得,,所以平面的一个法向量为,
因为,
所以,
所以平面平面.
方法归纳
判断平面与平面垂直有两种思路,一是利用判定定理判断;二是转化为平面的法向量进行判断.
2. 如图所示,已知平面,四边形为矩形,,,分别为,的中点.求证:
(1) 平面;
[答案] 如图所示,以为坐标原点,,,所在的直线分别为,,轴建立空间直角坐标系.
设,,则,,,,,因为,分别为,的中点,所以,,
所以,,,
所以.
又因为平面,所以平面.
(2) 平面平面.
[答案] 由(1)可知,,.
设平面的法向量为,
则即
令,得,,
则.
设平面的法向量为,
则即
令,得,,则.
因为,
所以,
所以平面平面.
题型3 利用空间向量求空间距离
例3 如图,在四棱锥中,是以为斜边的等腰直角三角形,,,,为的中点.
(1) 证明:平面;
[答案] 证明:取的中点,连接,
为的中点,,,四边形为平行四边形,,
平面,平面,平面.
[答案] 取的中点,连接,易得四边形为正方形,.
是以为斜边的等腰直角三角形,,,
,,平面,
平面.
,平面.
(2) 求点到的距离;
平面,平面平面.
以为原点,所在直线分别为轴,在平面内,作平面,建立如图所示的空间直角坐标系,
则,,,.
平面,.
在中,,
,,
,,
,,故,
故点A到的距离.
(3) 求直线到平面的距离.
[答案] 由(1)知平面,点到平面的距离即为所求.
由(2)知,,,
设平面的法向量为,
则即
令,则,,
,
点到平面的距离,
故直线到平面的距离为.
方法归纳
(1)求点到平面的距离,常常利用向量法,将问题转化为平面外一点与平面内一点构成的向量在平面的法向量方向上的投影向量的长度问题.(2)求直线到平面的距离,往往转化为点到平面的距离求解,且这个点要适当选取,以易于求解为准则.
3. 四棱锥中,四边形为正方形,平面,,,分别为,的中点.
[答案] 证明:以为原点,建立如图所示的空间直角坐标系,
由题意知,,,,,
(1) 求证:平面;
,,,
设平面的法向量为,
则
令,得,,
,
,
平面.
(2) 求点到平面的距离.
[答案] 由(1)知平面,点到平面的距离等于点到平面的距离.
由(1)知平面的一个法向量为,,
点到平面的距离,
点到平面的距离为,即点到平面的距离为.
题型4 利用空间向量求空间角
例4 如图所示,在四棱柱中,侧棱底面,平面,,,,,为棱的中点.
(1) 证明:;
[答案] 证明:如图所示,以为原点,,,所在直线分别为轴,轴,轴建立空间直角坐标系,
依题意得,,,,,,
所以,,因为,所以.
(2) 求平面与平面夹角的正弦值;
[答案] 设平面的法向量为,因为,
所以
取,可得,,所以.
由(1)知,又,且,,平
面,所以平面,
故为平面的一个法向量,
所以,
所以,
故平面与平面夹角的正弦值为.
(3) 设点在线段上,且直线与平面所成角的正弦值为,求线段的长.
[答案] 易得,,
设,,则,
易知为平面的一个法向量,
设为直线与平面所成的角,
则,
所以(负值舍去),则,
所以.故的长为.
方法归纳
解决立体几何中的夹角问题的思路:思路一:利用定义,在图形中找出所求的角,解三角形求出所求的角;思路二:利用向量法,转化为直线的方向向量与平面的法向量之间的夹角.
4. [2021山东济南第十一中学期中] 如图,在四棱锥中,底面,,,,,点为棱的中点.
(1) 证明:;
[答案] 证明:以点为原点建立空间直角坐标系.
则,,,,,,
所以,,
因为,
所以.
(2) 求直线与平面所成角的正弦值;
[答案] 易知,.
设为平面的法向量,
则即
令,得为平面的一个法向量,
所以,所以直线与平面所成角的正弦值为.
(3) 若为棱上一点,且满足,求平面与平面夹角的余弦值.
[答案] 易知,,,.
由点在棱上,设,,故.
得,因此,解得,即
,
设为平面的法向量,则即
令,得为平面的一个法向量.
易知平面的法向量为,则,
所以平面与平面夹角的余弦值为.
题型5 空间向量中的探索性问题
例5 [2020天津滨海七校高二联考] 如图,在三棱柱中,平面,已知,,,点是棱的中点.
(1) 求证:平面;
[答案] 证明:,,,,
,,
平面,又平面,
又,,平面,
平面.
(2) 求平面与平面夹角的余弦值;
[答案] 以为原点,,,的方向分别为,,轴的正方向建立如图所示的空间直角坐标系,
则,,,,,
设平面的法向量为,
,,
令,则,,.
设平面的法向量为,
,,
令,则,,
,
,
平面与平面夹角的余弦值为.
(3) 在棱上是否存在一点,使得与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
[答案] 假设存在点,设,
,,
,,.
由(2)知平面的一个法向量为,
由,得,即
,
或,
或.
方法归纳
解决探索性问题的基本策略是:通常假设题中的数学对象存在(或结论成立),然后在这个前提下进行逻辑推理,若能推导出与条件吻合的数据或事实,则说明假设成立,即存在,并可进一步证明;若推导出与条件或实际情况相矛盾的结论,则说明假设不成立,即不存在.
5. [2021山东聊城高二期中] 如图所示,在三棱柱中,平面,,,是的中点.
(1) 求直线与平面所成角的正弦值;
[答案] 建立如图所示的空间直角坐标系,
则,,,,所以,
,.
设平面的法向量为,则即令,则,
所以,
所以直线与平面所成角的正弦值为.
(2) 在棱上是否存在一点,使得平面与平面所成的角为若存在,求出点的坐标;若不存在,请说明理由.
[答案] 假设在棱上存在一点,使得平面与平面所成的角为,设,,则,
设平面的法向量为,
则即取,则.
由(1)知平面的法向量为.
所以,即,
解得(负值舍去).
故在棱上存在一点,使得平面与平面所成的角为,点的坐标为.
1. [2018课标Ⅱ理,9,5分] 在长方体中,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
C
2. [2020新高考Ⅰ,20,12分] 如图,四棱锥的底面为正方形,底面.设平面与平面的交线为.
(1) 证明:平面;
[答案] 证明:因为在正方形中,,
且平面,平面,
所以平面,
又因为平面,平面平面,所以,
因为在四棱锥中,底面是正方形,所以,所以,
又底面,底面,所以,所以,
因为,,平面,所以平面.
(2) 已知,为上的点,求与平面所成角的正弦值的最大值.
[答案] 建立如图所示的空间直角坐标系,
因为,所以,,,,,
设,则,,,
设平面的法向量为,
则即
令,则,,所以平面的一个法向量为,
则,
所以与平面所成角的正弦值为,当且仅当
时取等号,
所以当点的坐标为(1,0,1)时,直线与平面所成角的正弦值的最大值为.
3. [2020课标Ⅲ理,19,12分] 如图,在长方体中,点,分别在棱,上,且,.
(1) 证明:点在平面内;
[答案] 证明:在棱上取点,使得,连接,
在长方体中,且,,且,
,,,,
四边形为平行四边形,则且,
同理可得四边形为平行四边形,
且,
且,则四边形为平行四边形,
点在平面内.
(2) 若,,,求平面与平面夹角的正弦值.
[答案] 以点为坐标原点,所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系,
、、、,
,,,,
设平面的法向量为,
由得取,得,则
,
设平面的法向量为,
由得取,得,,则,
,
设平面与平面的夹角为,则,.
故平面与平面夹角的正弦值为.
4. [2018天津,17,13分] 如图,且,,且,且,平面,.
(1) 若为的中点,为的中点,求证:平面;
[答案] 证明:易知,,.
设为平面的法向量,
则即
不妨令,可得.
因为,
且平面,所以平面.
(2) 求平面与平面夹角的正弦值;
[答案] 易知,,.
设为平面的法向量,
则即
不妨令,可得
设为平面的法向量,
则即
不妨令,可得.
所以,故,
所以平面与平面夹角的正弦值为.
(3) 若点在线段上,且直线与平面所成的角为,求线段的长.
[答案] 设线段的长为,则点的坐标为,可得.
易知为平面的一个法向量,
故,
由题意可得,解得,所以线段的长为.
第一章 空间向量与立体几何
章末总结
题型1 空间向量的运算
例1 如图,在斜三棱柱中,向量,,,三个向量之间的夹角均为,点分别在上,且,,,,.
(1) 将向量用向量表示,并求;
[答案] ,
因为,
所以,
所以.
(2) 将向量用表示.
[答案] 因为,所以为的中点,
所以.
方法归纳
在几何体中,根据图形的特点,选择公共起点最集中的向量中的三个不共面的向量作为基底或选择有公共起点且关系最明确(如夹角或线段的长度)的三个不共面的向量作为基底,这样更利于解题.
1. 如图,在四棱锥中,底面是边长为1的正方形,到的距离都等于2.给出以下结论:①;②;③;④,其中正确结论的序号是_________ .
②③
[解析] 易知,所以②中结论正确;因为底面ABCD是边长为1的正方形,,所以,,又,所以,所以③中结论正确;显然①、④中结论不正确.故正确结论的序号是②③.
题型2 利用空间向量解决平行与垂直问题
例2 [2021天津高二期中] 如图,在四棱锥中,底面是正方形,底面,是的中点,已知,.
[答案] 因为是的中点,所以的坐标为(1,1,1),
所以,
易知,所以,
所以,即.
(1) 求证:;
[答案] 因为底面是正方形,所以,
因为底面,底面,
所以,因为,,平面,所以平面,
所以平面的一个法向量为,
设平面的法向量为,易知,
(2) 求证:平面平面.
则取,得,,所以平面的一个法向量为,
因为,
所以,
所以平面平面.
方法归纳
判断平面与平面垂直有两种思路,一是利用判定定理判断;二是转化为平面的法向量进行判断.
2. 如图所示,已知平面,四边形为矩形,,,分别为,的中点.求证:
(1) 平面;
[答案] 如图所示,以为坐标原点,,,所在的直线分别为,,轴建立空间直角坐标系.
设,,则,,,,,因为,分别为,的中点,所以,,
所以,,,
所以.
又因为平面,所以平面.
(2) 平面平面.
[答案] 由(1)可知,,.
设平面的法向量为,
则即
令,得,,
则.
设平面的法向量为,
则即
令,得,,则.
因为,
所以,
所以平面平面.
题型3 利用空间向量求空间距离
例3 如图,在四棱锥中,是以为斜边的等腰直角三角形,,,,为的中点.
(1) 证明:平面;
[答案] 证明:取的中点,连接,
为的中点,,,四边形为平行四边形,,
平面,平面,平面.
[答案] 取的中点,连接,易得四边形为正方形,.
是以为斜边的等腰直角三角形,,,
,,平面,
平面.
,平面.
(2) 求点到的距离;
平面,平面平面.
以为原点,所在直线分别为轴,在平面内,作平面,建立如图所示的空间直角坐标系,
则,,,.
平面,.
在中,,
,,
,,
,,故,
故点A到的距离.
(3) 求直线到平面的距离.
[答案] 由(1)知平面,点到平面的距离即为所求.
由(2)知,,,
设平面的法向量为,
则即
令,则,,
,
点到平面的距离,
故直线到平面的距离为.
方法归纳
(1)求点到平面的距离,常常利用向量法,将问题转化为平面外一点与平面内一点构成的向量在平面的法向量方向上的投影向量的长度问题.(2)求直线到平面的距离,往往转化为点到平面的距离求解,且这个点要适当选取,以易于求解为准则.
3. 四棱锥中,四边形为正方形,平面,,,分别为,的中点.
[答案] 证明:以为原点,建立如图所示的空间直角坐标系,
由题意知,,,,,
(1) 求证:平面;
,,,
设平面的法向量为,
则
令,得,,
,
,
平面.
(2) 求点到平面的距离.
[答案] 由(1)知平面,点到平面的距离等于点到平面的距离.
由(1)知平面的一个法向量为,,
点到平面的距离,
点到平面的距离为,即点到平面的距离为.
题型4 利用空间向量求空间角
例4 如图所示,在四棱柱中,侧棱底面,平面,,,,,为棱的中点.
(1) 证明:;
[答案] 证明:如图所示,以为原点,,,所在直线分别为轴,轴,轴建立空间直角坐标系,
依题意得,,,,,,
所以,,因为,所以.
(2) 求平面与平面夹角的正弦值;
[答案] 设平面的法向量为,因为,
所以
取,可得,,所以.
由(1)知,又,且,,平
面,所以平面,
故为平面的一个法向量,
所以,
所以,
故平面与平面夹角的正弦值为.
(3) 设点在线段上,且直线与平面所成角的正弦值为,求线段的长.
[答案] 易得,,
设,,则,
易知为平面的一个法向量,
设为直线与平面所成的角,
则,
所以(负值舍去),则,
所以.故的长为.
方法归纳
解决立体几何中的夹角问题的思路:思路一:利用定义,在图形中找出所求的角,解三角形求出所求的角;思路二:利用向量法,转化为直线的方向向量与平面的法向量之间的夹角.
4. [2021山东济南第十一中学期中] 如图,在四棱锥中,底面,,,,,点为棱的中点.
(1) 证明:;
[答案] 证明:以点为原点建立空间直角坐标系.
则,,,,,,
所以,,
因为,
所以.
(2) 求直线与平面所成角的正弦值;
[答案] 易知,.
设为平面的法向量,
则即
令,得为平面的一个法向量,
所以,所以直线与平面所成角的正弦值为.
(3) 若为棱上一点,且满足,求平面与平面夹角的余弦值.
[答案] 易知,,,.
由点在棱上,设,,故.
得,因此,解得,即
,
设为平面的法向量,则即
令,得为平面的一个法向量.
易知平面的法向量为,则,
所以平面与平面夹角的余弦值为.
题型5 空间向量中的探索性问题
例5 [2020天津滨海七校高二联考] 如图,在三棱柱中,平面,已知,,,点是棱的中点.
(1) 求证:平面;
[答案] 证明:,,,,
,,
平面,又平面,
又,,平面,
平面.
(2) 求平面与平面夹角的余弦值;
[答案] 以为原点,,,的方向分别为,,轴的正方向建立如图所示的空间直角坐标系,
则,,,,,
设平面的法向量为,
,,
令,则,,.
设平面的法向量为,
,,
令,则,,
,
,
平面与平面夹角的余弦值为.
(3) 在棱上是否存在一点,使得与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
[答案] 假设存在点,设,
,,
,,.
由(2)知平面的一个法向量为,
由,得,即
,
或,
或.
方法归纳
解决探索性问题的基本策略是:通常假设题中的数学对象存在(或结论成立),然后在这个前提下进行逻辑推理,若能推导出与条件吻合的数据或事实,则说明假设成立,即存在,并可进一步证明;若推导出与条件或实际情况相矛盾的结论,则说明假设不成立,即不存在.
5. [2021山东聊城高二期中] 如图所示,在三棱柱中,平面,,,是的中点.
(1) 求直线与平面所成角的正弦值;
[答案] 建立如图所示的空间直角坐标系,
则,,,,所以,
,.
设平面的法向量为,则即令,则,
所以,
所以直线与平面所成角的正弦值为.
(2) 在棱上是否存在一点,使得平面与平面所成的角为若存在,求出点的坐标;若不存在,请说明理由.
[答案] 假设在棱上存在一点,使得平面与平面所成的角为,设,,则,
设平面的法向量为,
则即取,则.
由(1)知平面的法向量为.
所以,即,
解得(负值舍去).
故在棱上存在一点,使得平面与平面所成的角为,点的坐标为.
1. [2018课标Ⅱ理,9,5分] 在长方体中,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
C
2. [2020新高考Ⅰ,20,12分] 如图,四棱锥的底面为正方形,底面.设平面与平面的交线为.
(1) 证明:平面;
[答案] 证明:因为在正方形中,,
且平面,平面,
所以平面,
又因为平面,平面平面,所以,
因为在四棱锥中,底面是正方形,所以,所以,
又底面,底面,所以,所以,
因为,,平面,所以平面.
(2) 已知,为上的点,求与平面所成角的正弦值的最大值.
[答案] 建立如图所示的空间直角坐标系,
因为,所以,,,,,
设,则,,,
设平面的法向量为,
则即
令,则,,所以平面的一个法向量为,
则,
所以与平面所成角的正弦值为,当且仅当
时取等号,
所以当点的坐标为(1,0,1)时,直线与平面所成角的正弦值的最大值为.
3. [2020课标Ⅲ理,19,12分] 如图,在长方体中,点,分别在棱,上,且,.
(1) 证明:点在平面内;
[答案] 证明:在棱上取点,使得,连接,
在长方体中,且,,且,
,,,,
四边形为平行四边形,则且,
同理可得四边形为平行四边形,
且,
且,则四边形为平行四边形,
点在平面内.
(2) 若,,,求平面与平面夹角的正弦值.
[答案] 以点为坐标原点,所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系,
、、、,
,,,,
设平面的法向量为,
由得取,得,则
,
设平面的法向量为,
由得取,得,,则,
,
设平面与平面的夹角为,则,.
故平面与平面夹角的正弦值为.
4. [2018天津,17,13分] 如图,且,,且,且,平面,.
(1) 若为的中点,为的中点,求证:平面;
[答案] 证明:易知,,.
设为平面的法向量,
则即
不妨令,可得.
因为,
且平面,所以平面.
(2) 求平面与平面夹角的正弦值;
[答案] 易知,,.
设为平面的法向量,
则即
不妨令,可得
设为平面的法向量,
则即
不妨令,可得.
所以,故,
所以平面与平面夹角的正弦值为.
(3) 若点在线段上,且直线与平面所成的角为,求线段的长.
[答案] 设线段的长为,则点的坐标为,可得.
易知为平面的一个法向量,
故,
由题意可得,解得,所以线段的长为.
