1.2.1 函数的概念 课件-2021-2022学年高一上学期数学 人教A版必修1(共19张PPT)
文档属性
| 名称 | 1.2.1 函数的概念 课件-2021-2022学年高一上学期数学 人教A版必修1(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 552.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 08:14:37 | ||
图片预览






文档简介
(共19张PPT)
课前准备
全力投入会使你与众不同
你是最优秀的,你一定能做的更好!
请拿出你的学案、课本、双色笔和草稿纸,还有你的激情!
1.2.1函数的概念
1、理解函数概念,会判断两个函数为同一函数的方法。
2、了解构成函数的三要素,理解和使用符号f(x)
3、培养理解抽象概念的能力,增强学习的积极性。
学习目标
目标引领课堂!
1.在初中我们学习了哪几种基本函数?其函数解析式分别是什么?
问题提出
2.初中对函数概念是怎样定义的?
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一次函数: ;
二次函数: ;
反比例函数:
知识探究(一)
一枚炮弹发射后,经过26s落到地面击中目标.炮弹的射高为845m,且炮弹距离地面的高度h(单位:m)随时间t(单位:s)变化的规律是:h=130t-5t2.
思考1:这里的变量t的变化范围是什么?变量h的变化范围是什么?试用集合表示?
A={t|0≤t≤26},B={h|0≤h≤845}
思考2:高度变量h与时间变量t之间的对应关系是否为函数?若是,其自变量是什么?
思考3:炮弹在空中的运行轨迹是什么?射高845m是怎样得到的?
知识探究(二)
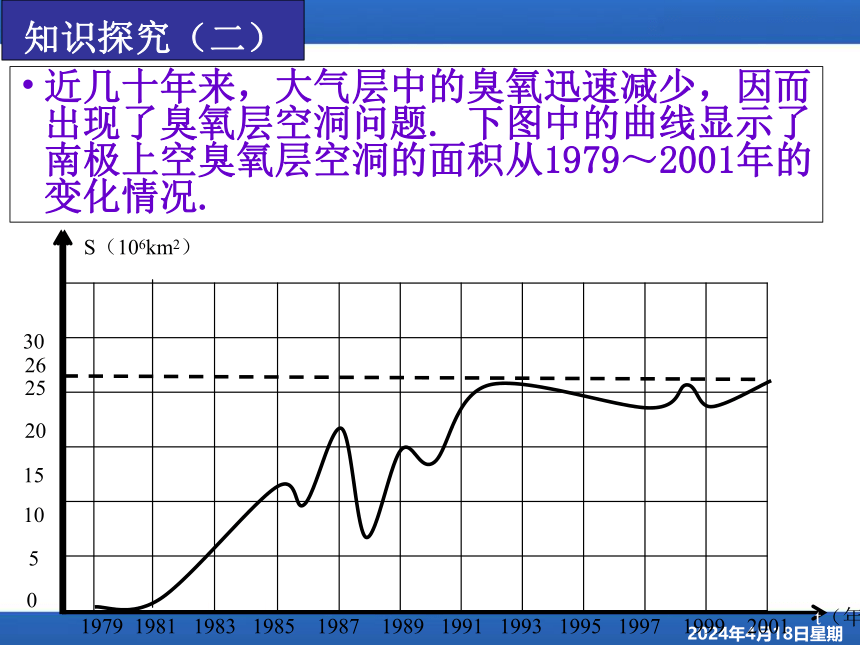
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题. 下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
S(106km2)
15
t(年)
5
1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
0
10
20
25
30
26
思考1:根据曲线分析,时间t的变化范围是什么?臭氧层空洞面积S的变化范围是什么?试用集合表示?
A={t|1979≤t≤2001};B={s|0≤s≤26}
思考2:时间变量t与臭氧层空洞面积S之间的对应关系是否为函数?若是,其自变量是什么?
思考3:这里表示函数关系的方式与上例有什么不同?
知识探究(三)
国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.下表是“八五”计划以来我国城镇居民恩格尔系数变化情况.
时间 (年) 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
恩格尔 系数 (%) 53.8 52.9 50.1 49.9 49.9 48.6 46.4 44.5 41.9 39.2 37.9
思考1:用t表示时间,r表示恩格尔系数,那么t和r的变化范围分别是什么?
A={1991,1992,…,2001},B={53.8,52.9,50.1,49.9,48.6,46.4,44.5,41.9,39.2,37.9}
思考2:时间变量t与恩格尔系数r之间的对应关系是否为函数?
不同点
实例(1)是用解析式刻画变量之间的对应关系,
实例(2)是用图象刻画变量之间的对应关系,
实例(3)是用表格刻画变量之间的对应关系.
共同点
(1)都有两个非空数集
(2)两个数集之间都有一种确定的对应关系
对于数集A中的每一个x,按照某种对应关系f ,在数集B中都有唯一确定的y和它对应,记作 f: A→B.
二、课本的实例
思考2:上述三个实例中变量之间的关系都是函数,那么从集合与对应的观点分析,函数还可以怎样定义?
设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,
那么就称f:A→B为从集合A到集合B的一个函数,记作 y=f(x),x∈A.
其中,x叫做自变量, x的取值范围A叫做函数的定义域;与x值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
例题讲解
例1:高一(22)班的同学组成集合A,教室里的凳子组成集合B,每一位同学都有唯一的一个凳子。这能否算作一个函数的例子,为什么?
例题2:下列可作为函数y= f (x)的图象的是
A B C D
x
x
x
x
y
y
y
y
O
O
O
O
√
练习: 判断下列关系式是否是函数?并说明理由。
思考3:在从集合A到集合B的一个函数f:A→B中,集合A是函数的定义域,集合B是函数的值域吗?
例如:
定义域为{0,1,2},值域为{0,2,4}
思考4:一个函数由哪几个部分组成?
定义域、对应关系、值域;
定义域相同,对应关系完全一致,则两个函数相等.
函数的值域由函数的定义域和对应关系所确定;
举例:
思考5:如果给定函数的定义域和对应关系,那么函数的值域确定吗?
思考6:两个函数相等的条件是什么?
例3、对于函数y=f (x),以下说法正确的有( )
①y是x的函数
②对于不同的x,y的值也不同
③ f(a)表示当x=a时,函数f(x)的值,是一个常量
④ f(x)一定可以用一个具体的式子表示出来
A、1个 B、2个 C、3个 D、4个
B
例4、以下4种说法:
①定义域相同,值域相同的两个函数相等。
②若函数的定义域只含有一个元素,则值域也只有一个元素
③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立
④定义域和对应关系确定后,函数值也就确定了 正确有( )
A、1个 B、2个 C、3个 D、4个
C
课堂小结
同学们说说看,你这一节课有哪些收获?
课前准备
全力投入会使你与众不同
你是最优秀的,你一定能做的更好!
请拿出你的学案、课本、双色笔和草稿纸,还有你的激情!
1.2.1函数的概念
1、理解函数概念,会判断两个函数为同一函数的方法。
2、了解构成函数的三要素,理解和使用符号f(x)
3、培养理解抽象概念的能力,增强学习的积极性。
学习目标
目标引领课堂!
1.在初中我们学习了哪几种基本函数?其函数解析式分别是什么?
问题提出
2.初中对函数概念是怎样定义的?
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一次函数: ;
二次函数: ;
反比例函数:
知识探究(一)
一枚炮弹发射后,经过26s落到地面击中目标.炮弹的射高为845m,且炮弹距离地面的高度h(单位:m)随时间t(单位:s)变化的规律是:h=130t-5t2.
思考1:这里的变量t的变化范围是什么?变量h的变化范围是什么?试用集合表示?
A={t|0≤t≤26},B={h|0≤h≤845}
思考2:高度变量h与时间变量t之间的对应关系是否为函数?若是,其自变量是什么?
思考3:炮弹在空中的运行轨迹是什么?射高845m是怎样得到的?
知识探究(二)
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题. 下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
S(106km2)
15
t(年)
5
1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
0
10
20
25
30
26
思考1:根据曲线分析,时间t的变化范围是什么?臭氧层空洞面积S的变化范围是什么?试用集合表示?
A={t|1979≤t≤2001};B={s|0≤s≤26}
思考2:时间变量t与臭氧层空洞面积S之间的对应关系是否为函数?若是,其自变量是什么?
思考3:这里表示函数关系的方式与上例有什么不同?
知识探究(三)
国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.下表是“八五”计划以来我国城镇居民恩格尔系数变化情况.
时间 (年) 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
恩格尔 系数 (%) 53.8 52.9 50.1 49.9 49.9 48.6 46.4 44.5 41.9 39.2 37.9
思考1:用t表示时间,r表示恩格尔系数,那么t和r的变化范围分别是什么?
A={1991,1992,…,2001},B={53.8,52.9,50.1,49.9,48.6,46.4,44.5,41.9,39.2,37.9}
思考2:时间变量t与恩格尔系数r之间的对应关系是否为函数?
不同点
实例(1)是用解析式刻画变量之间的对应关系,
实例(2)是用图象刻画变量之间的对应关系,
实例(3)是用表格刻画变量之间的对应关系.
共同点
(1)都有两个非空数集
(2)两个数集之间都有一种确定的对应关系
对于数集A中的每一个x,按照某种对应关系f ,在数集B中都有唯一确定的y和它对应,记作 f: A→B.
二、课本的实例
思考2:上述三个实例中变量之间的关系都是函数,那么从集合与对应的观点分析,函数还可以怎样定义?
设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,
那么就称f:A→B为从集合A到集合B的一个函数,记作 y=f(x),x∈A.
其中,x叫做自变量, x的取值范围A叫做函数的定义域;与x值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
例题讲解
例1:高一(22)班的同学组成集合A,教室里的凳子组成集合B,每一位同学都有唯一的一个凳子。这能否算作一个函数的例子,为什么?
例题2:下列可作为函数y= f (x)的图象的是
A B C D
x
x
x
x
y
y
y
y
O
O
O
O
√
练习: 判断下列关系式是否是函数?并说明理由。
思考3:在从集合A到集合B的一个函数f:A→B中,集合A是函数的定义域,集合B是函数的值域吗?
例如:
定义域为{0,1,2},值域为{0,2,4}
思考4:一个函数由哪几个部分组成?
定义域、对应关系、值域;
定义域相同,对应关系完全一致,则两个函数相等.
函数的值域由函数的定义域和对应关系所确定;
举例:
思考5:如果给定函数的定义域和对应关系,那么函数的值域确定吗?
思考6:两个函数相等的条件是什么?
例3、对于函数y=f (x),以下说法正确的有( )
①y是x的函数
②对于不同的x,y的值也不同
③ f(a)表示当x=a时,函数f(x)的值,是一个常量
④ f(x)一定可以用一个具体的式子表示出来
A、1个 B、2个 C、3个 D、4个
B
例4、以下4种说法:
①定义域相同,值域相同的两个函数相等。
②若函数的定义域只含有一个元素,则值域也只有一个元素
③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立
④定义域和对应关系确定后,函数值也就确定了 正确有( )
A、1个 B、2个 C、3个 D、4个
C
课堂小结
同学们说说看,你这一节课有哪些收获?
