6.2.1空间向量基本定理 - 2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第二册)(共14张PPT)
文档属性
| 名称 | 6.2.1空间向量基本定理 - 2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第二册)(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 543.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
6.2.1空间向量基本定理
学习目标
1.必备知识:了解空间向量基本定理及其推论;理解空间向量的基底、基向量的概念;理解空间任一向量可用空间不共面的三个已知向量唯一线性表出
2.关键能力:能利用空间向量基本定理解决简单的几何问题
3.活动体验:学会用发展的眼光看问题,认识到事物都是在不断的发展、变化的,会用联系的观点看待事物.
情景引入
复习引入
平面内,如果两个向量 a, b不共线, 那么平面内任一向量c ,存在惟一的有序实数对(x, y), 使c=xa+yb. {a,b}为一组基底.
平面向量的基本定理(共面向量定理)
平面向量的基本定理(共面向量定理)给我们哪些启示?
B
C
A
D
A1
B1
C1
D1
情景引入
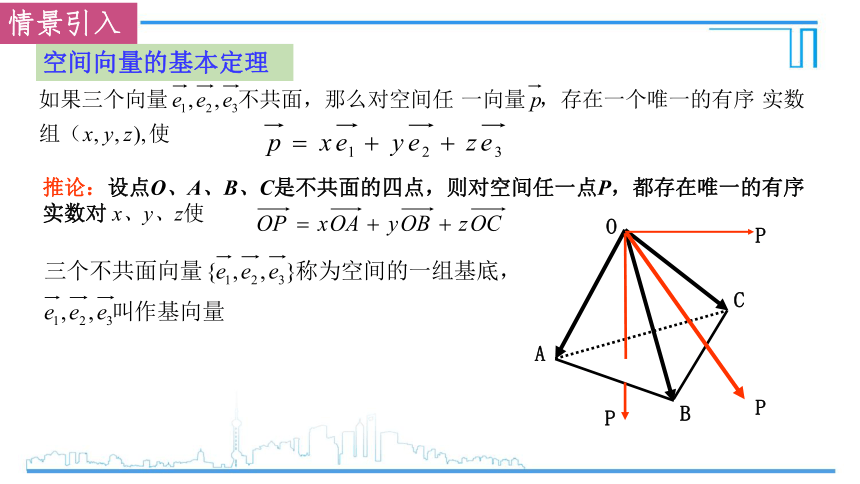
空间向量的基本定理
推论:设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数对 x、y、z使
O
A
B
C
P
P
P
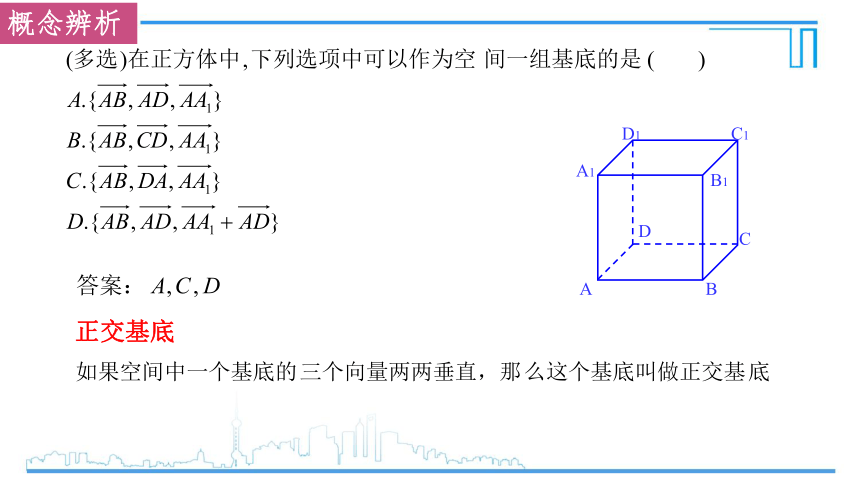
概念辨析
B
C
A
D
A1
B1
C1
D1
正交基底
数学应用
数学应用
数学应用
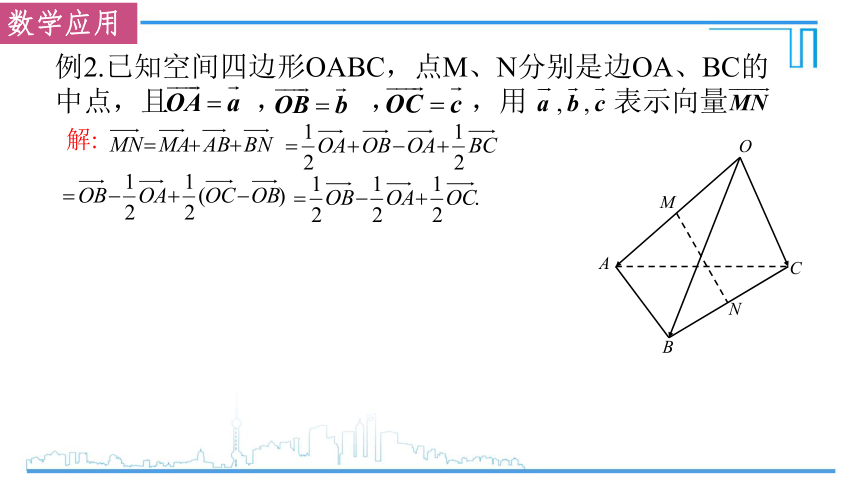
例2.已知空间四边形OABC,点M、N分别是边OA、BC的中点,且 , , ,用 表示向量
O
A
B
C
M
N
解:
数学应用
变式. 如图, M, N 分别是四面体 OABC 的边 OA, BC 的中点, P, Q 是 MN 的三等分点. 用向量 表示 和
O
A
B
C
M
N
P
Q
解:
数学应用
课堂小结
空 间 向 量 的 基 本 定 理
推论:设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数对 x、y、z使
O
A
B
C
P
P
P
空间向量的基本定理作用
统一的表示空间中的每一个向量
课堂达标
课堂达标
课堂达标
情景引入
谢 谢 观 看
6.2.1空间向量基本定理
学习目标
1.必备知识:了解空间向量基本定理及其推论;理解空间向量的基底、基向量的概念;理解空间任一向量可用空间不共面的三个已知向量唯一线性表出
2.关键能力:能利用空间向量基本定理解决简单的几何问题
3.活动体验:学会用发展的眼光看问题,认识到事物都是在不断的发展、变化的,会用联系的观点看待事物.
情景引入
复习引入
平面内,如果两个向量 a, b不共线, 那么平面内任一向量c ,存在惟一的有序实数对(x, y), 使c=xa+yb. {a,b}为一组基底.
平面向量的基本定理(共面向量定理)
平面向量的基本定理(共面向量定理)给我们哪些启示?
B
C
A
D
A1
B1
C1
D1
情景引入
空间向量的基本定理
推论:设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数对 x、y、z使
O
A
B
C
P
P
P
概念辨析
B
C
A
D
A1
B1
C1
D1
正交基底
数学应用
数学应用
数学应用
例2.已知空间四边形OABC,点M、N分别是边OA、BC的中点,且 , , ,用 表示向量
O
A
B
C
M
N
解:
数学应用
变式. 如图, M, N 分别是四面体 OABC 的边 OA, BC 的中点, P, Q 是 MN 的三等分点. 用向量 表示 和
O
A
B
C
M
N
P
Q
解:
数学应用
课堂小结
空 间 向 量 的 基 本 定 理
推论:设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数对 x、y、z使
O
A
B
C
P
P
P
空间向量的基本定理作用
统一的表示空间中的每一个向量
课堂达标
课堂达标
课堂达标
情景引入
谢 谢 观 看
