1.4.1正弦函数、余弦函数(人教A版必修4)
文档属性
| 名称 | 1.4.1正弦函数、余弦函数(人教A版必修4) |  | |
| 格式 | zip | ||
| 文件大小 | 732.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-10 21:57:30 | ||
图片预览




文档简介
课件20张PPT。1.4.1正弦函数、余弦函数
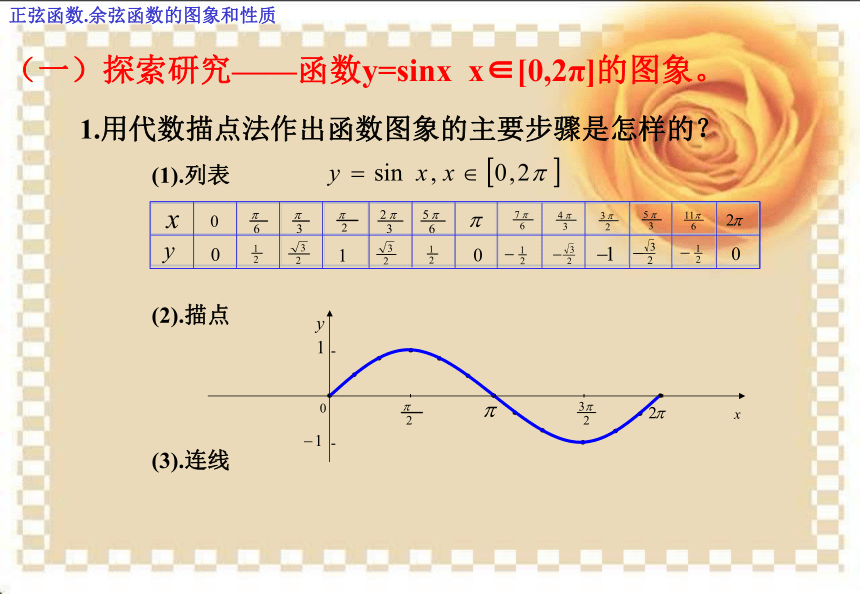
的图象和性质人教A版必修4(第一课时)引入: 潮汐与港口的变化关系图(1).列表(2).描点(3).连线1.用代数描点法作出函数图象的主要步骤是怎样的?(一)探索研究——函数y=sinx x∈[0,2π]的图象。 正弦函数.余弦函数的图象和性质. . . .利用三角函数线
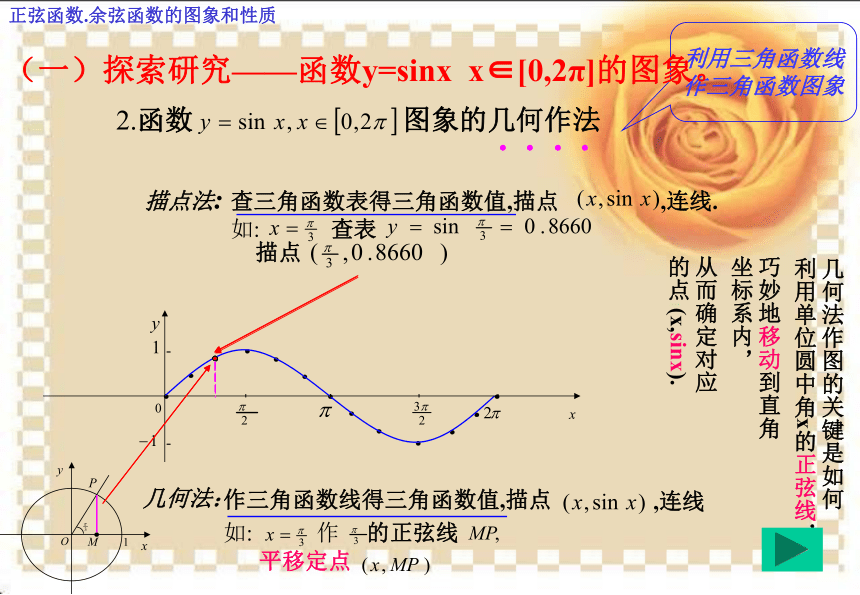
作三角函数图象描点法:查表如:描点几何法:如:平移定点几何法作图的关键是如何利用单位圆中角x的正弦线,
巧妙地移动到直角坐标系内,从而确定对应的点1(x,sinx).
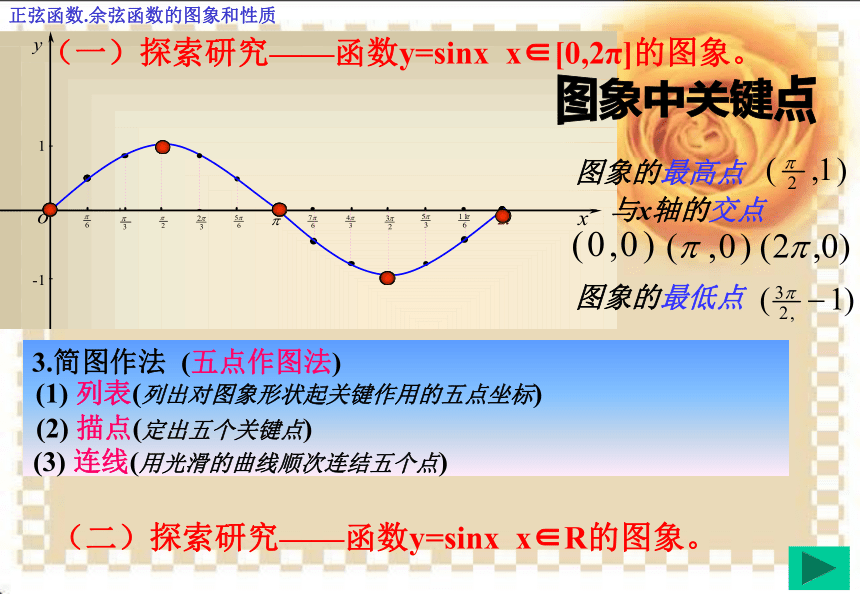
(一)探索研究——函数y=sinx x∈[0,2π]的图象。 正弦函数.余弦函数的图象和性质与x轴的交点图象的最高点图象的最低点图象中关键点3.简图作法
(五点作图法)(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)(一)探索研究——函数y=sinx x∈[0,2π]的图象。 (二)探索研究——函数y=sinx x∈R的图象。 正弦函数.余弦函数的图象和性质与x轴的交点图象的最高点图象的最低点与x轴的交点图象的最高点图象的最低点简图作法
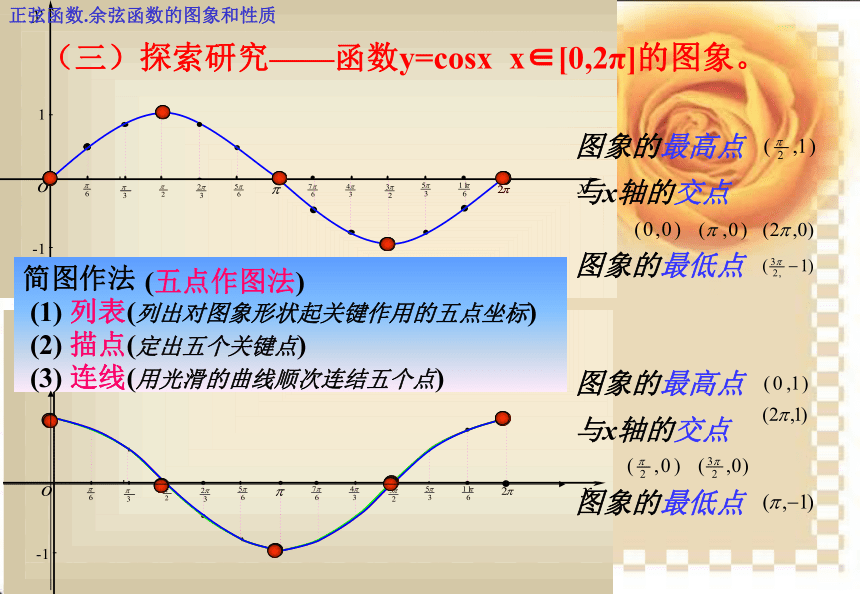
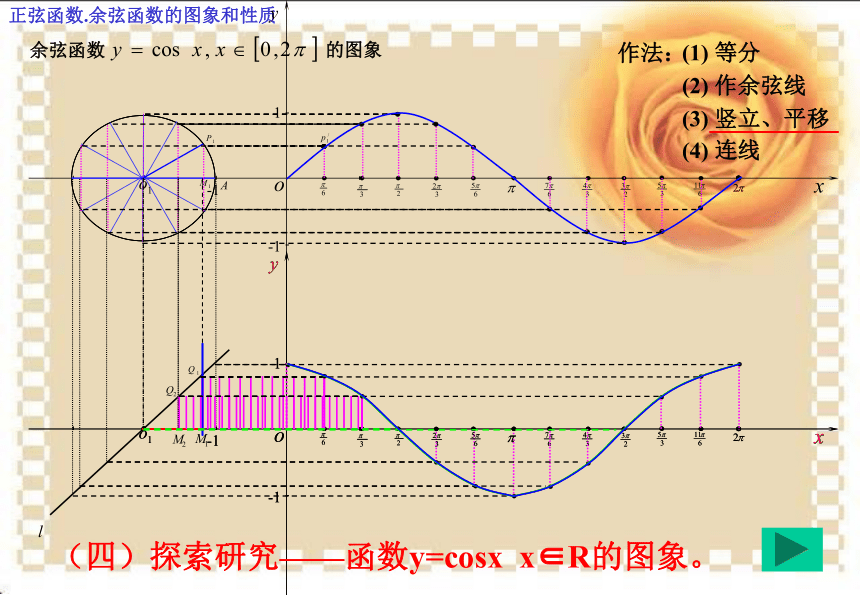
(五点作图法)(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)(三)探索研究——函数y=cosx x∈[0,2π]的图象。 (四)探索研究——函数y=cosx x∈R的图象。 正弦曲线余弦曲线正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质[-1,1][-1,1]RR因为终边相同的角的三角函数值相同,所以y=sinx的图象在……,
……与y=sinx,x∈[0,2π]的图象相同因为终边相同的角的三角函数值相同,所以y=cosx的图象在……,
……与y=cosx,x∈[0,2π]的图象相同正弦曲线余弦曲线正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质T=2πT=2π[-1,1][-1,1]RRy=sinxy=sinx (x?R) 图象关于原点对称正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质关于原点对称关于y轴对称T=2πT=2π[-1,1][-1,1]RR 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z正弦函数.余弦函数的图象和性质 余弦函数的单调性 y=cosx (x?R)正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质关于原点对称关于y轴对称T=2πT=2π[-1,1][-1,1]RR正弦函数.余弦函数的图象和性质作函数y=sinx+1,x∈[0,2π]的简图解:列表描点作图练习 作函数 y=-sinx,x∈[0,2π]的简图思考题 作函数 y=2sin2x-1,x∈[0,2π]的简图思考 函数 y=sinx, y=sinx+1, y=-sinx, x∈[0,2π]的
图象有什么关系?(六)例题讲解y=sinx+1y=-sinxy=sinx小结:
本节课我们学习了用单位圆中的正弦线作正弦函数,通过诱导公式得到余弦函数的图象,用五点法作正弦函数和余弦函数的简图
P52习题第1题六、课后作业:再见!
的图象和性质人教A版必修4(第一课时)引入: 潮汐与港口的变化关系图(1).列表(2).描点(3).连线1.用代数描点法作出函数图象的主要步骤是怎样的?(一)探索研究——函数y=sinx x∈[0,2π]的图象。 正弦函数.余弦函数的图象和性质. . . .利用三角函数线
作三角函数图象描点法:查表如:描点几何法:如:平移定点几何法作图的关键是如何利用单位圆中角x的正弦线,
巧妙地移动到直角坐标系内,从而确定对应的点1(x,sinx).
(一)探索研究——函数y=sinx x∈[0,2π]的图象。 正弦函数.余弦函数的图象和性质与x轴的交点图象的最高点图象的最低点图象中关键点3.简图作法
(五点作图法)(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)(一)探索研究——函数y=sinx x∈[0,2π]的图象。 (二)探索研究——函数y=sinx x∈R的图象。 正弦函数.余弦函数的图象和性质与x轴的交点图象的最高点图象的最低点与x轴的交点图象的最高点图象的最低点简图作法
(五点作图法)(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)(三)探索研究——函数y=cosx x∈[0,2π]的图象。 (四)探索研究——函数y=cosx x∈R的图象。 正弦曲线余弦曲线正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质[-1,1][-1,1]RR因为终边相同的角的三角函数值相同,所以y=sinx的图象在……,
……与y=sinx,x∈[0,2π]的图象相同因为终边相同的角的三角函数值相同,所以y=cosx的图象在……,
……与y=cosx,x∈[0,2π]的图象相同正弦曲线余弦曲线正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质T=2πT=2π[-1,1][-1,1]RRy=sinxy=sinx (x?R) 图象关于原点对称正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质关于原点对称关于y轴对称T=2πT=2π[-1,1][-1,1]RR 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z正弦函数.余弦函数的图象和性质 余弦函数的单调性 y=cosx (x?R)正弦函数.余弦函数的图象和性质正弦函数.余弦函数的图象和性质(五)探索研究——函数y=sinx ,
y=cosx 的性质关于原点对称关于y轴对称T=2πT=2π[-1,1][-1,1]RR正弦函数.余弦函数的图象和性质作函数y=sinx+1,x∈[0,2π]的简图解:列表描点作图练习 作函数 y=-sinx,x∈[0,2π]的简图思考题 作函数 y=2sin2x-1,x∈[0,2π]的简图思考 函数 y=sinx, y=sinx+1, y=-sinx, x∈[0,2π]的
图象有什么关系?(六)例题讲解y=sinx+1y=-sinxy=sinx小结:
本节课我们学习了用单位圆中的正弦线作正弦函数,通过诱导公式得到余弦函数的图象,用五点法作正弦函数和余弦函数的简图
P52习题第1题六、课后作业:再见!
