第6章实数复习课件22021-2022学年人教版七年级数学下册(38张ppt)
文档属性
| 名称 | 第6章实数复习课件22021-2022学年人教版七年级数学下册(38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 10:22:16 | ||
图片预览









文档简介
(共38张PPT)
实数 章末复习
七年级下册
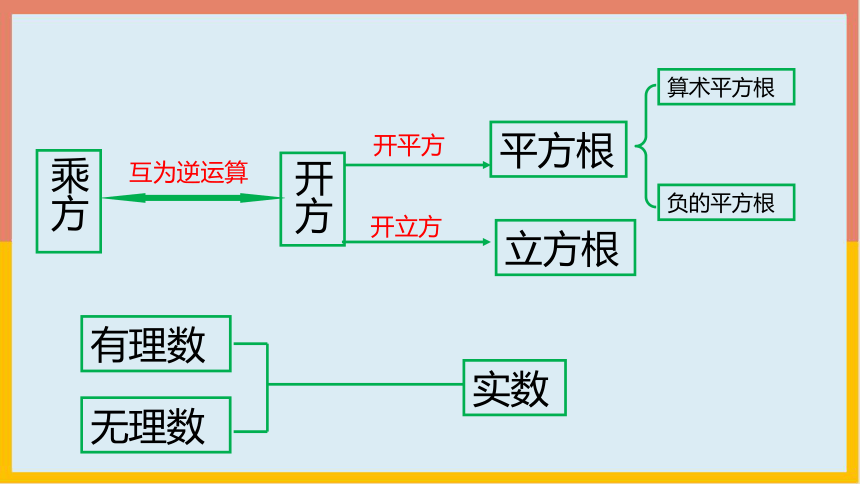
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
1.算术平方根的定义:
一般地,如果一个正数x的平方等于a,即=a,那么这个正数x叫做a的算术平方根。a的算术平方根记为,读作“根号a”,a叫做被开方数。
特殊:0的算术平方根是0。
一般地,如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根).
这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.a的平方根记为±
2. 平方根的定义:
3.平方根的性质:
正数有2个平方根,它们互为相反数;0的平方根是0;负数没有平方根。
4.立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作.
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
1、平方根的定义:若x2=a,则x就叫做a的__________。
a的平方根用________表示
2、平方根的性质
(1)一个正数有 平方根,它们互为________
(2)0的平方根还是____
(3)负数______平方根
3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2
即
1、立方根的定义:若x3=a,则x就叫做a的________。
a的立方根用________表示
2、立方根的性质
(1)一个正数的立方根___________
(2)0的立方根还是_____
(3)负数的立方根________
3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2
即
2
相反数
0
没有
是正数
是负数
0
平方根
立方根
平方根与立方根
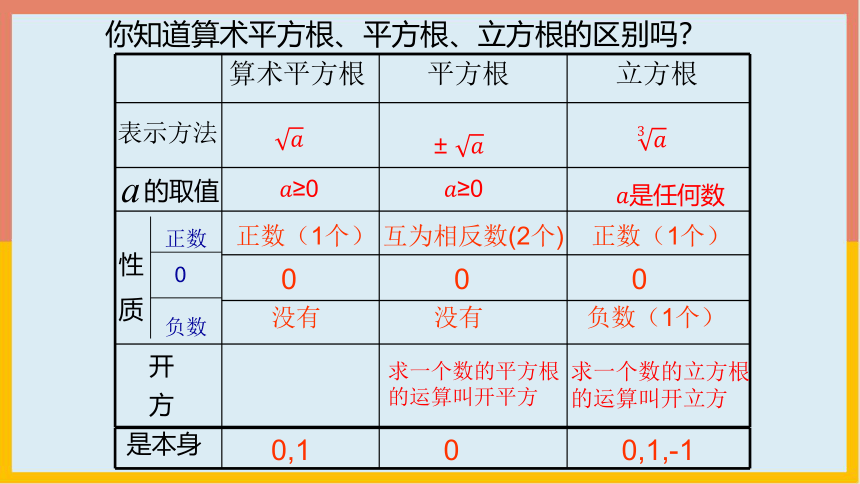
你知道算术平方根、平方根、立方根的区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥0
开
方
≥0
正数
0
负数
正数(1个)
0
没有
互为相反数(2个)
0
没有
正数(1个)
0
负数(1个)
求一个数的平方根的运算叫开平方
求一个数的立方根的运算叫开立方
是本身
0,1
0
0,1,-1
1、—8是_______的平方根; 64的平方根是_______ ;
;-64的立方根是_____ ;
的平方根是 。
2、 的立方根是______,它的平方根是 __________.
64
±8
8
-4
3
2
3.当x __________时,2x-1没有平方根
5.一个正数x的两个平方根分别是a+1和a-3,则a=__________, x=__________.
<0.5
x=7
1
4
6、化简:
_______; ________; ________.
8、如果一个数的平方根是a+3和2a-15,求这个数的立方根。
=3
=
几个基本公式:(注意字母
的取值范围)
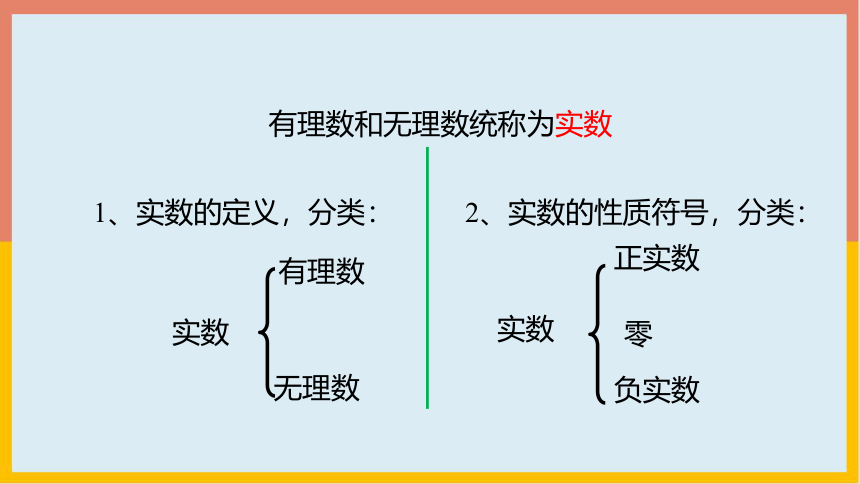
2、实数的性质符号,分类:
有理数和无理数统称为实数
实数
有理数
无理数
实数
正实数
负实数
零
1、实数的定义,分类:
在进行实数的运算时,有理数的运算法则及运算性质同样适用。
实数与____________上的点是一一对应的,
反过来数轴上的点与实数一一对应的关系
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
数轴
无限不循环的小数 叫做无理数.
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.下列各数中有理数是___________________________________
0.3737737773……,.
,
有理数集合
无理数集合
2.把下列各数分别填入相应的集合内: , (相邻两个3之间的7的个数逐次加1)
3.判断下列说法是否正确:
(1)无限小数都是无理数;
(2)无理数都是无限小数;
(3)带根号的数都是无理数;
(4)实数都是无理数;
(5)无理数都是实数;
(6)没有根号的数都是有理数.
×
√
×
×
√
×
4,.
5、数轴上两点A,B分别表示实数和-1,求A,B两点之间的距离。
6、如果在数轴上表示1, 的对应点分别为A、 B, 点B关于点A的对称点为点C,点C关于点A的对称点为点B(即AC=AB),则点C所表示的数是( )
7、_____________________.
A、 B、 C、 D、
C
0、、 2、 3、-4
1、相反数、(负)倒数、绝对值
在实数范围内,相反数、倒数、绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。例如: a、b互为相反数,c与d互为倒数则a+1+b+cd= 。
2
2、比较大小的方法
有理化法 估算法 求差法
1、填空:
(1)
(2) 的倒数是 ;
(3) -2的绝对值是 ;
(4)__________.
2、已知实数a、b在数轴上对应点的位置如图所示。化简:
2
2
8或-6
2-
b a o
x
=-2b
3、实数的大小比较
(1)与; (2)与;
(3)与; (4);
解:(1)<;
(2)<;
(3)>;
(4)>.
实数的计算:
在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
计算
; (2) ;
(3) ; (4).
解:;
(2)
(3) = = ;
(4) = =
1、
2、π的整数部分为3,则它的小数部分是____________;
3、
11.18
0.3535
π-3
解:由题意得:=3,= -3= -1
= 3[3 -( -1 )] =12-
4、解方程:
;
;
.
注意:
(1)将括号看作一个整体;
(2)开平方有两个值,开立方只有一个值。
解:(1)5或1;
(2)= ;
(3)=
5、填空:
(1)________________;
(2) ____________.
式子有意义:
1、在开平方运算中,被开方数具有非负性
2、分母不为0
0
1、下列说法正确的是( )
A
B表示6的算术平方根的相反数
C 任何数都有平方根
D一定没有平方根
2、_____________
3、_____________
_____________
B
-5
x≤0
x为任何实数
4、
5、已知等腰三角形的两边长满足,求三角形的周长
解:由题意得:解得:
,y=1 ∴2+3 y =4
解:由题意,得解得:
所以等腰三角形的三边为2,2,3或2,3,3
所以,三角形的周长为7或8
6、已知,求的值.
7、已知,求 y-x的算术平方根
解:由题意得:-4≥0解得≥4
∴-3+ ,
∴-4=9
∴=13
解:由题意,得:
∴ =2
当=2时,y=3
8、
解:由题意,得: 解得:
解:由题意,得:解得:
9、
10、(1) ______________;
(2) ______________;
(3),则的值是______________.
11、如果一个数的平方根为+1和2 -7, 求这个数.
12、已知5+ 的小数部分为 , 7- 的小数部分为,求的值.
解:由题意得
解得: =2
=3 =9
这个数为9
解:由题意得: 5+ -8= -3
= 7- -2= 5-
= -3+ 5- = + 2-
13、计算:
(1); (2);
(3); (4).
解: (1)
=
=
(2)
=
=
(3)
=4-3-22
=-3
(4)
=
=
14、解方程:
; ;
.
或
解:
-8
15、计算:
(1);
(2);
(3);
(4).
解: (1) ;
(2) 若则=-1;
(3) = 25;
(4)=2013
书面作业:完成相关书本作业
再见
实数 章末复习
七年级下册
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
1.算术平方根的定义:
一般地,如果一个正数x的平方等于a,即=a,那么这个正数x叫做a的算术平方根。a的算术平方根记为,读作“根号a”,a叫做被开方数。
特殊:0的算术平方根是0。
一般地,如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根).
这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.a的平方根记为±
2. 平方根的定义:
3.平方根的性质:
正数有2个平方根,它们互为相反数;0的平方根是0;负数没有平方根。
4.立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作.
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
1、平方根的定义:若x2=a,则x就叫做a的__________。
a的平方根用________表示
2、平方根的性质
(1)一个正数有 平方根,它们互为________
(2)0的平方根还是____
(3)负数______平方根
3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2
即
1、立方根的定义:若x3=a,则x就叫做a的________。
a的立方根用________表示
2、立方根的性质
(1)一个正数的立方根___________
(2)0的立方根还是_____
(3)负数的立方根________
3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2
即
2
相反数
0
没有
是正数
是负数
0
平方根
立方根
平方根与立方根
你知道算术平方根、平方根、立方根的区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥0
开
方
≥0
正数
0
负数
正数(1个)
0
没有
互为相反数(2个)
0
没有
正数(1个)
0
负数(1个)
求一个数的平方根的运算叫开平方
求一个数的立方根的运算叫开立方
是本身
0,1
0
0,1,-1
1、—8是_______的平方根; 64的平方根是_______ ;
;-64的立方根是_____ ;
的平方根是 。
2、 的立方根是______,它的平方根是 __________.
64
±8
8
-4
3
2
3.当x __________时,2x-1没有平方根
5.一个正数x的两个平方根分别是a+1和a-3,则a=__________, x=__________.
<0.5
x=7
1
4
6、化简:
_______; ________; ________.
8、如果一个数的平方根是a+3和2a-15,求这个数的立方根。
=3
=
几个基本公式:(注意字母
的取值范围)
2、实数的性质符号,分类:
有理数和无理数统称为实数
实数
有理数
无理数
实数
正实数
负实数
零
1、实数的定义,分类:
在进行实数的运算时,有理数的运算法则及运算性质同样适用。
实数与____________上的点是一一对应的,
反过来数轴上的点与实数一一对应的关系
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
数轴
无限不循环的小数 叫做无理数.
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.下列各数中有理数是___________________________________
0.3737737773……,.
,
有理数集合
无理数集合
2.把下列各数分别填入相应的集合内: , (相邻两个3之间的7的个数逐次加1)
3.判断下列说法是否正确:
(1)无限小数都是无理数;
(2)无理数都是无限小数;
(3)带根号的数都是无理数;
(4)实数都是无理数;
(5)无理数都是实数;
(6)没有根号的数都是有理数.
×
√
×
×
√
×
4,.
5、数轴上两点A,B分别表示实数和-1,求A,B两点之间的距离。
6、如果在数轴上表示1, 的对应点分别为A、 B, 点B关于点A的对称点为点C,点C关于点A的对称点为点B(即AC=AB),则点C所表示的数是( )
7、_____________________.
A、 B、 C、 D、
C
0、、 2、 3、-4
1、相反数、(负)倒数、绝对值
在实数范围内,相反数、倒数、绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。例如: a、b互为相反数,c与d互为倒数则a+1+b+cd= 。
2
2、比较大小的方法
有理化法 估算法 求差法
1、填空:
(1)
(2) 的倒数是 ;
(3) -2的绝对值是 ;
(4)__________.
2、已知实数a、b在数轴上对应点的位置如图所示。化简:
2
2
8或-6
2-
b a o
x
=-2b
3、实数的大小比较
(1)与; (2)与;
(3)与; (4);
解:(1)<;
(2)<;
(3)>;
(4)>.
实数的计算:
在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
计算
; (2) ;
(3) ; (4).
解:;
(2)
(3) = = ;
(4) = =
1、
2、π的整数部分为3,则它的小数部分是____________;
3、
11.18
0.3535
π-3
解:由题意得:=3,= -3= -1
= 3[3 -( -1 )] =12-
4、解方程:
;
;
.
注意:
(1)将括号看作一个整体;
(2)开平方有两个值,开立方只有一个值。
解:(1)5或1;
(2)= ;
(3)=
5、填空:
(1)________________;
(2) ____________.
式子有意义:
1、在开平方运算中,被开方数具有非负性
2、分母不为0
0
1、下列说法正确的是( )
A
B表示6的算术平方根的相反数
C 任何数都有平方根
D一定没有平方根
2、_____________
3、_____________
_____________
B
-5
x≤0
x为任何实数
4、
5、已知等腰三角形的两边长满足,求三角形的周长
解:由题意得:解得:
,y=1 ∴2+3 y =4
解:由题意,得解得:
所以等腰三角形的三边为2,2,3或2,3,3
所以,三角形的周长为7或8
6、已知,求的值.
7、已知,求 y-x的算术平方根
解:由题意得:-4≥0解得≥4
∴-3+ ,
∴-4=9
∴=13
解:由题意,得:
∴ =2
当=2时,y=3
8、
解:由题意,得: 解得:
解:由题意,得:解得:
9、
10、(1) ______________;
(2) ______________;
(3),则的值是______________.
11、如果一个数的平方根为+1和2 -7, 求这个数.
12、已知5+ 的小数部分为 , 7- 的小数部分为,求的值.
解:由题意得
解得: =2
=3 =9
这个数为9
解:由题意得: 5+ -8= -3
= 7- -2= 5-
= -3+ 5- = + 2-
13、计算:
(1); (2);
(3); (4).
解: (1)
=
=
(2)
=
=
(3)
=4-3-22
=-3
(4)
=
=
14、解方程:
; ;
.
或
解:
-8
15、计算:
(1);
(2);
(3);
(4).
解: (1) ;
(2) 若则=-1;
(3) = 25;
(4)=2013
书面作业:完成相关书本作业
再见
