安徽省安庆市宿松县新安初级中学201-2022学年上学期九年级期末数学模拟试卷(word版,含答案)
文档属性
| 名称 | 安徽省安庆市宿松县新安初级中学201-2022学年上学期九年级期末数学模拟试卷(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 22:47:10 | ||
图片预览


文档简介
绝密★启用前
新安初级中学201-2022学年度九年级期末数学模拟试卷
一、选择题(本大题共10小题,共40分)
如果线段,,那么和的比例中项是
A. B. C. D.
下列各式中表示二次函数的是
A. B. C. D.
如图,在平面直角坐标系中,是反比例函数的图象上的一点,则矩形的面积为
A.
B.
C.
D.
若为锐角,且,则为
A. B. C. D.
将抛物线向右平移个单位后,抛物线的解析式为
A. B. C. D.
设,,是抛物线上的三点,则,,的大小关系为
A. B. C. D.
如图,与都是正方形网格中的格点三角形顶点在格点上,那么与的周长比为
A.
B. :
C. :
D. :
如图,一个边长分别为、、的直角三角形的一个顶点与正方形的顶点重合,另两个顶点分别在正方形的两条边、上,那么这个正方形的面积是
A. B. C. D.
如图所示,已知,为反比例函数图象上的两点,动点在轴正半轴上运动,当线段与线段之差达到最大时,点的坐标是
A. B. C. D.
如图,在中,,以其三边为边分别向外作正方形,延长,分别交,于点,,连结交于点,若,,则的长为
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
抛物线与轴交于两点,分别是,,则______.
如图,点在二次函数第一象限的图象上,轴,轴,垂足分别为、,连接,交函数图象于点,轴于点,则的值为______.
如图,四边形和四边形都是平行四边形,点为的中点,分别交和于点,若的面积为,则图中阴影部分的面积为___________.
在平面直角坐标系中,点的坐标为,点为,若为线段上一动点,则的最小值是 .
三、解答题(本大题共9小题,共90分)
(8分)计算:
(8分)已知线段、、满足,且.
求、、的值
若线段是线段、的比例中项,求的值.
(8分)在平面直角坐标系中,的三个顶点的坐标分别是,,.
画出关于轴成轴对称的;
在网格内以点为位似中心,使与的位似比为:,请画出.
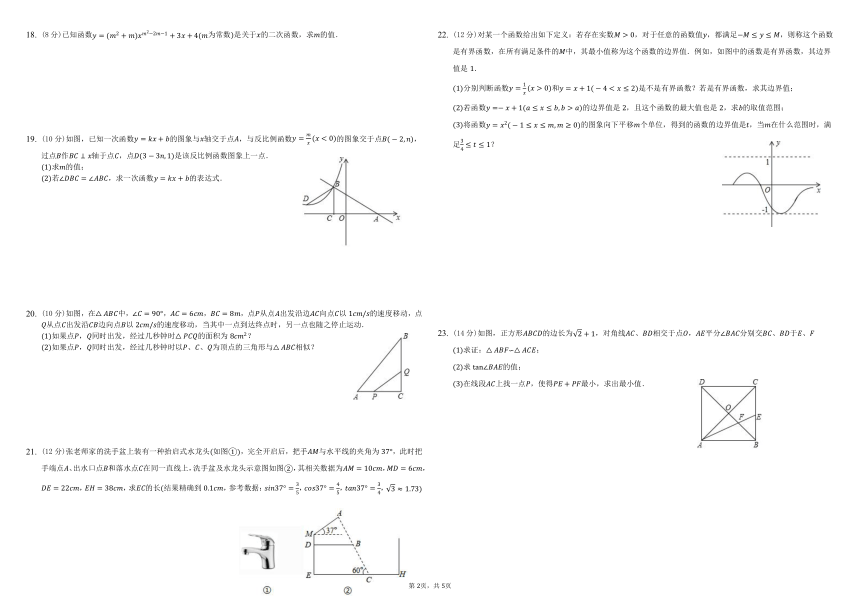
(8分)已知函数为常数是关于的二次函数,求的值.
(10分)如图,已知一次函数的图象与轴交于点,与反比例函数的图象交于点,过点作轴于点,点是该反比例函数图象上一点.
求的值;
若,求一次函数的表达式.
(10分)如图,在中,,,,点从点出发沿边向点以的速度移动,点从点出发沿边向点以的速度移动,当其中一点到达终点时,另一点也随之停止运动.
如果点,同时出发,经过几秒钟时的面积为?
如果点,同时出发,经过几秒钟时以、、为顶点的三角形与相似?
(12分)张老师家的洗手盆上装有一种抬启式水龙头如图,完全开启后,把手与水平线的夹角为,此时把手端点、出水口点和落水点在同一直线上,洗手盆及水龙头示意图如图,其相关数据为,,,,求的长结果精确到,参考数据:,,,
(12分)对某一个函数给出如下定义:若存在实数,对于任意的函数值,都满足,则称这个函数是有界函数,在所有满足条件的中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是.
分别判断函数和是不是有界函数?若是有界函数,求其边界值;
若函数的边界值是,且这个函数的最大值也是,求的取值范围;
将函数的图象向下平移个单位,得到的函数的边界值是,当在什么范围时,满足?
(14分)如图,正方形的边长为,对角线、相交于点,平分分别交、于、
求证:∽;
求的值;
在线段上找一点,使得最小,求出最小值.
答案
1.【答案】D2.【答案】B3.【答案】B4.【答案】A5.【答案】C
6.【答案】A7.【答案】A8.【答案】D9.【答案】D10.【答案】A
11.【答案】212.【答案】13.【答案】714.【答案】
15.【答案】解:原式=-1-(-1)+1+2×+2
=-1-+1+1++2
=3.
16.【答案】解:(1)设===k(k0),
则a=3k,b=2k,c=6k.
因为a+2b+c=26,
所以3k+22k+6k=26,解得k=2,
所以a=32=6,b=22=4,c=62=12.
(2)因为线段x是线段a、b的比例中项,
所以=ab=64=24,
所以x=2(舍负).
17.【答案】解:如图所示:
18.【答案】解:根据题意,得
,
解得,
∴m=3.
19.【答案】解:(1)∵点B(-2,n)、D(3-3n,1)在反比例函数y=(x<0)的图象上,
∴,
解得:.
(2)由(1)知反比例函数解析式为y=-,
∵n=3,
∴点B(-2,3)、D(-6,1),
如图,过点D作DE⊥BC于点E,延长DE交AB于点F,
在△DBE和△FBE中,
∵,
∴△DBE≌△FBE(ASA),
∴DE=FE=4,
∴点F(2,1),
将点B(-2,3)、F(2,1)代入y=kx+b,
∴,
解得:,
∴y=-x+2.
20.【答案】解:(1)设xs后,可使△PCQ的面积为8cm2.
由题意得,AP=xcm,PC=(6-x)cm,CQ=2xcm,
则(6-x) 2x=8,
整理得x2-6x+8=0,
解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设t秒后以P、C、Q为顶点的三角形与△ABC相似,则PC=6-t,QC=2t.
当△PCQ∽△ACB时,=,即=,
解得:t=.
当△PCQ∽△BCA时,=,即=,
解得:t=.
综上所述,当t=或t=时,以P、C、Q为顶点的三角形与△ABC相似.
21.【答案】解:过点A作AG⊥EH于G,过点M作MN⊥AG于N,如图所示,
则四边形MEGN为矩形,
∴EG=MN,NG=ME=MD+DE=6+22=28(cm),
在Rt△AMN中,sin∠AMN=,cos∠AMN=,
∴AN=AM×sin37°≈10×=6(cm),MN=AM×cos37°≈10×=8(cm),
∴EG=8cm,AG=AN+NG=6+28=34(cm),
∵∠ACG=60°,
∴CG===≈19.60(cm),
∴EC=EG+CG=8+19.60≈27.6(cm),
答:EC的长约为27.6cm.
22.【答案】解:(1)根据有界函数的定义知,函数y=( x>0)不是有界函数;
函数y=x+1(-4≤x≤2)是有界函数.
∵-4+1=-3,2+1=3,
∴y=x+1(-4<x≤2)边界值为3.
(2)∵k=-1<0,
∴函数y=-x+1的图象是y随x的增大而减小,
∴当x=a时,y=-a+1=2,
解得:a=-1;
当x=b时,y=-b+1,
∴,
∴-1<b≤3;
(3)若m>1,函数向下平移m个单位后,x=0时,函数值小于-1,
此时函数的边界t≥1,与题意不符,故m≤1.
当x=-1时,y=1,函数y=x2过点(-1,1);
当x=0时,y最小=0,函数y=x2过点(0,0).
都向下平移m个单位,则函数y=x2-m过点(-1,1-m)、(0,-m),
∵≤t≤1,
∴或,
解得:0≤m≤或≤m≤1.
故当0≤m≤或≤m≤1时,满足≤t≤1.
23.【答案】(1)证明:四边形ABCD是正方形,
ACE=ABF=CAB=,
AE平分CAB,
EAC=BAF=22.5,
ABF∽ACE;
(2)解:如图1中,作EHAC于H.
EA平分CAB,EHAC,EBAB,
BE=EH,
HCE=,CHE=,
HCE=HEC=,
HC=EH,
BE=EH=HC,设BE=HE=HC=x,则EC=x, 图1
BC=+1,
x+x=+1,
x=1,
在RtABE中,
ABE=,
EAB===-1.
(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小.
作EMBD于M.易知BM=EM=,
AC==2+,
OA=OC=OB=AC=,
OH=OF=OAOAF=OAEAB=(-1)=,
HM=OH+OM=,
在Rt△EHM中,EH===, 图2
PE+PF的最小值为.
第2页,共2页
第1页,共1页
新安初级中学201-2022学年度九年级期末数学模拟试卷
一、选择题(本大题共10小题,共40分)
如果线段,,那么和的比例中项是
A. B. C. D.
下列各式中表示二次函数的是
A. B. C. D.
如图,在平面直角坐标系中,是反比例函数的图象上的一点,则矩形的面积为
A.
B.
C.
D.
若为锐角,且,则为
A. B. C. D.
将抛物线向右平移个单位后,抛物线的解析式为
A. B. C. D.
设,,是抛物线上的三点,则,,的大小关系为
A. B. C. D.
如图,与都是正方形网格中的格点三角形顶点在格点上,那么与的周长比为
A.
B. :
C. :
D. :
如图,一个边长分别为、、的直角三角形的一个顶点与正方形的顶点重合,另两个顶点分别在正方形的两条边、上,那么这个正方形的面积是
A. B. C. D.
如图所示,已知,为反比例函数图象上的两点,动点在轴正半轴上运动,当线段与线段之差达到最大时,点的坐标是
A. B. C. D.
如图,在中,,以其三边为边分别向外作正方形,延长,分别交,于点,,连结交于点,若,,则的长为
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
抛物线与轴交于两点,分别是,,则______.
如图,点在二次函数第一象限的图象上,轴,轴,垂足分别为、,连接,交函数图象于点,轴于点,则的值为______.
如图,四边形和四边形都是平行四边形,点为的中点,分别交和于点,若的面积为,则图中阴影部分的面积为___________.
在平面直角坐标系中,点的坐标为,点为,若为线段上一动点,则的最小值是 .
三、解答题(本大题共9小题,共90分)
(8分)计算:
(8分)已知线段、、满足,且.
求、、的值
若线段是线段、的比例中项,求的值.
(8分)在平面直角坐标系中,的三个顶点的坐标分别是,,.
画出关于轴成轴对称的;
在网格内以点为位似中心,使与的位似比为:,请画出.
(8分)已知函数为常数是关于的二次函数,求的值.
(10分)如图,已知一次函数的图象与轴交于点,与反比例函数的图象交于点,过点作轴于点,点是该反比例函数图象上一点.
求的值;
若,求一次函数的表达式.
(10分)如图,在中,,,,点从点出发沿边向点以的速度移动,点从点出发沿边向点以的速度移动,当其中一点到达终点时,另一点也随之停止运动.
如果点,同时出发,经过几秒钟时的面积为?
如果点,同时出发,经过几秒钟时以、、为顶点的三角形与相似?
(12分)张老师家的洗手盆上装有一种抬启式水龙头如图,完全开启后,把手与水平线的夹角为,此时把手端点、出水口点和落水点在同一直线上,洗手盆及水龙头示意图如图,其相关数据为,,,,求的长结果精确到,参考数据:,,,
(12分)对某一个函数给出如下定义:若存在实数,对于任意的函数值,都满足,则称这个函数是有界函数,在所有满足条件的中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是.
分别判断函数和是不是有界函数?若是有界函数,求其边界值;
若函数的边界值是,且这个函数的最大值也是,求的取值范围;
将函数的图象向下平移个单位,得到的函数的边界值是,当在什么范围时,满足?
(14分)如图,正方形的边长为,对角线、相交于点,平分分别交、于、
求证:∽;
求的值;
在线段上找一点,使得最小,求出最小值.
答案
1.【答案】D2.【答案】B3.【答案】B4.【答案】A5.【答案】C
6.【答案】A7.【答案】A8.【答案】D9.【答案】D10.【答案】A
11.【答案】212.【答案】13.【答案】714.【答案】
15.【答案】解:原式=-1-(-1)+1+2×+2
=-1-+1+1++2
=3.
16.【答案】解:(1)设===k(k0),
则a=3k,b=2k,c=6k.
因为a+2b+c=26,
所以3k+22k+6k=26,解得k=2,
所以a=32=6,b=22=4,c=62=12.
(2)因为线段x是线段a、b的比例中项,
所以=ab=64=24,
所以x=2(舍负).
17.【答案】解:如图所示:
18.【答案】解:根据题意,得
,
解得,
∴m=3.
19.【答案】解:(1)∵点B(-2,n)、D(3-3n,1)在反比例函数y=(x<0)的图象上,
∴,
解得:.
(2)由(1)知反比例函数解析式为y=-,
∵n=3,
∴点B(-2,3)、D(-6,1),
如图,过点D作DE⊥BC于点E,延长DE交AB于点F,
在△DBE和△FBE中,
∵,
∴△DBE≌△FBE(ASA),
∴DE=FE=4,
∴点F(2,1),
将点B(-2,3)、F(2,1)代入y=kx+b,
∴,
解得:,
∴y=-x+2.
20.【答案】解:(1)设xs后,可使△PCQ的面积为8cm2.
由题意得,AP=xcm,PC=(6-x)cm,CQ=2xcm,
则(6-x) 2x=8,
整理得x2-6x+8=0,
解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设t秒后以P、C、Q为顶点的三角形与△ABC相似,则PC=6-t,QC=2t.
当△PCQ∽△ACB时,=,即=,
解得:t=.
当△PCQ∽△BCA时,=,即=,
解得:t=.
综上所述,当t=或t=时,以P、C、Q为顶点的三角形与△ABC相似.
21.【答案】解:过点A作AG⊥EH于G,过点M作MN⊥AG于N,如图所示,
则四边形MEGN为矩形,
∴EG=MN,NG=ME=MD+DE=6+22=28(cm),
在Rt△AMN中,sin∠AMN=,cos∠AMN=,
∴AN=AM×sin37°≈10×=6(cm),MN=AM×cos37°≈10×=8(cm),
∴EG=8cm,AG=AN+NG=6+28=34(cm),
∵∠ACG=60°,
∴CG===≈19.60(cm),
∴EC=EG+CG=8+19.60≈27.6(cm),
答:EC的长约为27.6cm.
22.【答案】解:(1)根据有界函数的定义知,函数y=( x>0)不是有界函数;
函数y=x+1(-4≤x≤2)是有界函数.
∵-4+1=-3,2+1=3,
∴y=x+1(-4<x≤2)边界值为3.
(2)∵k=-1<0,
∴函数y=-x+1的图象是y随x的增大而减小,
∴当x=a时,y=-a+1=2,
解得:a=-1;
当x=b时,y=-b+1,
∴,
∴-1<b≤3;
(3)若m>1,函数向下平移m个单位后,x=0时,函数值小于-1,
此时函数的边界t≥1,与题意不符,故m≤1.
当x=-1时,y=1,函数y=x2过点(-1,1);
当x=0时,y最小=0,函数y=x2过点(0,0).
都向下平移m个单位,则函数y=x2-m过点(-1,1-m)、(0,-m),
∵≤t≤1,
∴或,
解得:0≤m≤或≤m≤1.
故当0≤m≤或≤m≤1时,满足≤t≤1.
23.【答案】(1)证明:四边形ABCD是正方形,
ACE=ABF=CAB=,
AE平分CAB,
EAC=BAF=22.5,
ABF∽ACE;
(2)解:如图1中,作EHAC于H.
EA平分CAB,EHAC,EBAB,
BE=EH,
HCE=,CHE=,
HCE=HEC=,
HC=EH,
BE=EH=HC,设BE=HE=HC=x,则EC=x, 图1
BC=+1,
x+x=+1,
x=1,
在RtABE中,
ABE=,
EAB===-1.
(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小.
作EMBD于M.易知BM=EM=,
AC==2+,
OA=OC=OB=AC=,
OH=OF=OAOAF=OAEAB=(-1)=,
HM=OH+OM=,
在Rt△EHM中,EH===, 图2
PE+PF的最小值为.
第2页,共2页
第1页,共1页
同课章节目录
