22.1 二次函数课件-人教版九年级数学上册(18张ppt)
文档属性
| 名称 | 22.1 二次函数课件-人教版九年级数学上册(18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 10:26:21 | ||
图片预览






文档简介
(共18张PPT)
第二十二章 《二次函数》
单元起始课
从地面抛出一个小球,小球的高度h随小球运动时间t的变化而变化,h与t之间有什么关系?
情景1
t
h
o
一.创设情境,设问导入
情景2
李阿姨要用16米长的篱笆围成一个矩形的鸡圈,鸡圈的面积能是12平方米吗?16平方米呢?20平方米呢?怎样围可以使小鸡的活动范围最大?最大是多少?
思考:.
1.若一边长是x米,另一边长为y米,那么y与x之间的关系式________.
2.若鸡圈的面积为S平方米,S与x之间的关系式是____________.
S=-x2+8x
y=-x+8
一.创设情境,设问导入
1.(1)正方体六个面是全等的正方形,设正方体棱长为 x,正方体的所有棱长之
和L关于x的关系式:_______.
(2)表面积为 y,则 y 关于x 的关系式: .
y=6x2
L=12x
一.创设情境,设问导入
2.n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n
的关系式:____________
3.某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比
上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而
确定,y与x之间的关系式:_______________
问题
y=20x2+40x+20
思考:这些函数有什么共同特征
数学的概念应该怎么获得? “可以从大量同类事物的不同例证中 找到它们的共同的关键特征。” ------选摘自《数学概念的获得》一文
二.自主学习,研问探究
一次函数知识结构框图
一次函数
一元一次方程(不等式)
实际问题
概念
图象
性质
实际应用
联系
一元二次方程(不等式)
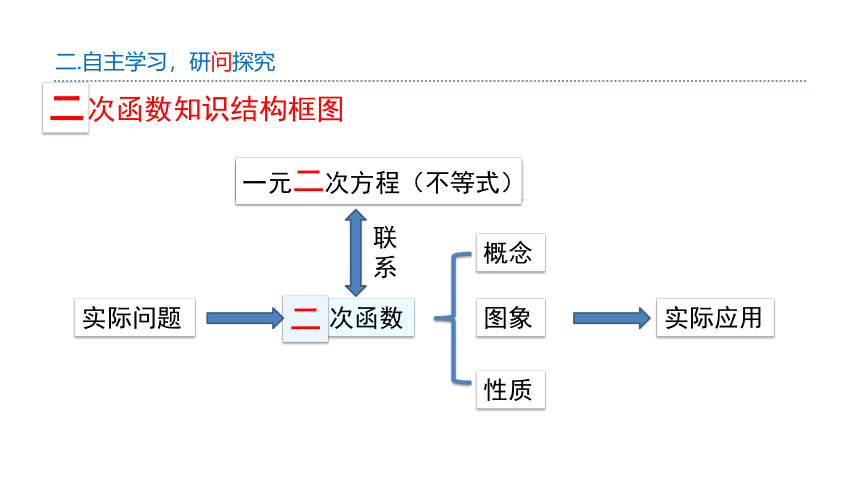
二.自主学习,研问探究
二
二
概念:
一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数,叫做二次函数。
其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项
二次函数的概念
二.自主学习,研问探究
画出二次函数y=x2的图象.
1. 列表:
2. 描点:
3. 连线:
数
形
二次函数的图象和性质
二.自主学习,研问探究
y=ax2 y=x2 y=-x2
图象
对称轴
顶点
开口方向
最值
增减性
二次函数的图象和性质
y轴
y轴
(0,0)
(0,0)
向上
向下
当x=0时,y最小值=0
当x=0时,y最大值=0
当x<0时,y随x取值的增大而减小;
当x>0时,y随x取值的增大而增大.
当x<0时,y随x取值的增大而增大;
当x>0时,y随x取值的增大而减小.
二.自主学习,研问探究
三.交流思想,解问展示
情景2
李阿姨要用16米长的篱笆围成一个矩形的鸡圈,鸡圈的面积能是12平方米吗?16平方米呢?20平方米呢?怎样围可以使小鸡的活动范围最大?
问题1:
鸡圈的面积能是12平方米吗?此时如何设计?
方法一:
一边x 1 2 3 4 5 6 7
面积S 12 12
7
15
16
15
7
2
12
6
12
方法二:
方法三:
三.交流思想,解问展示
二次函数与一元二次方程
问题2:鸡圈的面积能是16平方米吗?此时如何设计?
问题3:鸡圈的面积能是20平方米吗?
三.交流思想,解问展示
二次函数与一元二次方程
问题4:鸡圈如何设计,面积最大?
四.提炼规整,疑问解惑
实际问题与二次函数
当x=4时,
S最大值=16
A
E
B
C
D
1.下列函数是二次函数的是 ( )
A.y=2x+1 B. C.y=3x2+1 D.
C
五.当堂检测,习问反馈
2.已知,如图,在Rt三角形ABC中,∠C=90°,AC=BC=4,点D为AB边上的一个动点(不与A.B两点重合),过点D作DE垂直AC,垂足为点E,连接DC.
(1)设AD为x,EC为y时,y关于x的解析式是_______,y是x的____函数.
(2)设AE为x,三角形ACD的面积为y时,y关于x的解析式是_____,y是x的_____函数.
(3)在不添加辅助线的情况下,你能找到两个变量,使其中一个变量是另一个变量的二次函数吗?
设____为x,____为y时,y关于x的解析式是____,y是x的二次函数.
一次
一次
六.回眸课堂,质问升华
1.你学到了哪些知识?
2.用到了哪些方法
3.体会了哪些数学思想
知识
方法
思想
理解掌握二次函数的概念.
掌握研究函数的基本路径.
类比
转化
归纳
数形结合
建模思想
方程思想
函数思想
(1)在不添加辅助线的情况下,你能找到两个变量,使其中一个变量是另一个变量的二次函数吗?
设____为x,____为y时,y关于x的解析式是____,y是x的二次函数.
(2)从你写出的几个函数中选择一个进行类比探究.
布置作业
已知,如图,在Rt三角形ABC中,∠C=90°,AC=BC=4,点D为AB边上的一个动点(不与A.B两点重合),过点D作DE垂直AC,垂足为点E,连接DC.
A
E
B
C
D
寄语:
同学们, 不仅数学学习要遵循一定的路径,采用适当的方法,采撷数学的硕果,生活中也是这样,希望大家沿着勤奋的路径,采用科学的方法,采撷中考的硕果!
深表感谢,恳请指正
第二十二章 《二次函数》
单元起始课
从地面抛出一个小球,小球的高度h随小球运动时间t的变化而变化,h与t之间有什么关系?
情景1
t
h
o
一.创设情境,设问导入
情景2
李阿姨要用16米长的篱笆围成一个矩形的鸡圈,鸡圈的面积能是12平方米吗?16平方米呢?20平方米呢?怎样围可以使小鸡的活动范围最大?最大是多少?
思考:.
1.若一边长是x米,另一边长为y米,那么y与x之间的关系式________.
2.若鸡圈的面积为S平方米,S与x之间的关系式是____________.
S=-x2+8x
y=-x+8
一.创设情境,设问导入
1.(1)正方体六个面是全等的正方形,设正方体棱长为 x,正方体的所有棱长之
和L关于x的关系式:_______.
(2)表面积为 y,则 y 关于x 的关系式: .
y=6x2
L=12x
一.创设情境,设问导入
2.n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n
的关系式:____________
3.某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比
上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而
确定,y与x之间的关系式:_______________
问题
y=20x2+40x+20
思考:这些函数有什么共同特征
数学的概念应该怎么获得? “可以从大量同类事物的不同例证中 找到它们的共同的关键特征。” ------选摘自《数学概念的获得》一文
二.自主学习,研问探究
一次函数知识结构框图
一次函数
一元一次方程(不等式)
实际问题
概念
图象
性质
实际应用
联系
一元二次方程(不等式)
二.自主学习,研问探究
二
二
概念:
一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数,叫做二次函数。
其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项
二次函数的概念
二.自主学习,研问探究
画出二次函数y=x2的图象.
1. 列表:
2. 描点:
3. 连线:
数
形
二次函数的图象和性质
二.自主学习,研问探究
y=ax2 y=x2 y=-x2
图象
对称轴
顶点
开口方向
最值
增减性
二次函数的图象和性质
y轴
y轴
(0,0)
(0,0)
向上
向下
当x=0时,y最小值=0
当x=0时,y最大值=0
当x<0时,y随x取值的增大而减小;
当x>0时,y随x取值的增大而增大.
当x<0时,y随x取值的增大而增大;
当x>0时,y随x取值的增大而减小.
二.自主学习,研问探究
三.交流思想,解问展示
情景2
李阿姨要用16米长的篱笆围成一个矩形的鸡圈,鸡圈的面积能是12平方米吗?16平方米呢?20平方米呢?怎样围可以使小鸡的活动范围最大?
问题1:
鸡圈的面积能是12平方米吗?此时如何设计?
方法一:
一边x 1 2 3 4 5 6 7
面积S 12 12
7
15
16
15
7
2
12
6
12
方法二:
方法三:
三.交流思想,解问展示
二次函数与一元二次方程
问题2:鸡圈的面积能是16平方米吗?此时如何设计?
问题3:鸡圈的面积能是20平方米吗?
三.交流思想,解问展示
二次函数与一元二次方程
问题4:鸡圈如何设计,面积最大?
四.提炼规整,疑问解惑
实际问题与二次函数
当x=4时,
S最大值=16
A
E
B
C
D
1.下列函数是二次函数的是 ( )
A.y=2x+1 B. C.y=3x2+1 D.
C
五.当堂检测,习问反馈
2.已知,如图,在Rt三角形ABC中,∠C=90°,AC=BC=4,点D为AB边上的一个动点(不与A.B两点重合),过点D作DE垂直AC,垂足为点E,连接DC.
(1)设AD为x,EC为y时,y关于x的解析式是_______,y是x的____函数.
(2)设AE为x,三角形ACD的面积为y时,y关于x的解析式是_____,y是x的_____函数.
(3)在不添加辅助线的情况下,你能找到两个变量,使其中一个变量是另一个变量的二次函数吗?
设____为x,____为y时,y关于x的解析式是____,y是x的二次函数.
一次
一次
六.回眸课堂,质问升华
1.你学到了哪些知识?
2.用到了哪些方法
3.体会了哪些数学思想
知识
方法
思想
理解掌握二次函数的概念.
掌握研究函数的基本路径.
类比
转化
归纳
数形结合
建模思想
方程思想
函数思想
(1)在不添加辅助线的情况下,你能找到两个变量,使其中一个变量是另一个变量的二次函数吗?
设____为x,____为y时,y关于x的解析式是____,y是x的二次函数.
(2)从你写出的几个函数中选择一个进行类比探究.
布置作业
已知,如图,在Rt三角形ABC中,∠C=90°,AC=BC=4,点D为AB边上的一个动点(不与A.B两点重合),过点D作DE垂直AC,垂足为点E,连接DC.
A
E
B
C
D
寄语:
同学们, 不仅数学学习要遵循一定的路径,采用适当的方法,采撷数学的硕果,生活中也是这样,希望大家沿着勤奋的路径,采用科学的方法,采撷中考的硕果!
深表感谢,恳请指正
同课章节目录
