人教版七年级数学(下)——课件:5.1.3同位角内错角同旁内角(22张ppt)
文档属性
| 名称 | 人教版七年级数学(下)——课件:5.1.3同位角内错角同旁内角(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 10:36:46 | ||
图片预览



文档简介
(共22张PPT)
5.1.3 同位角 内错角 同旁内角
1.平面上两条直线有哪两种位置关系
(平行和相交)
2.两条直线相交有几个角
(4个)
3.两条直线与第三条直线相交呢?
(8个)
复习引入
观察图片,除了我们所学的两条直线相交外,有没有更多的直线相交呢?
画一画:如果三条直线相交,位置有哪几种呢?
A
C
B
D
E
F
7
1
2
3
4
5
6
8
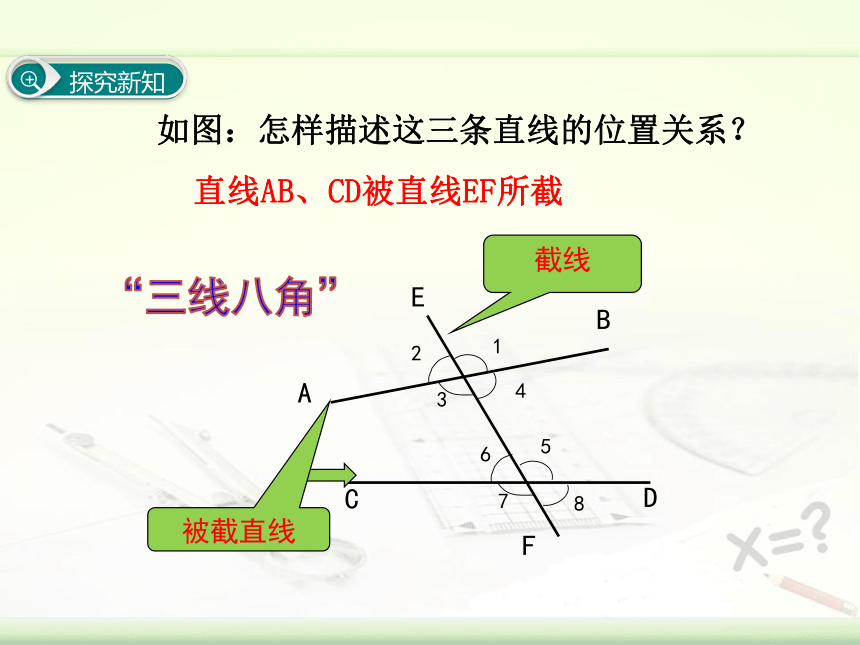
如图:怎样描述这三条直线的位置关系?
直线AB、CD被直线EF所截
截线
探究新知
1
5
2
6
3
7
4
8
a
b
c
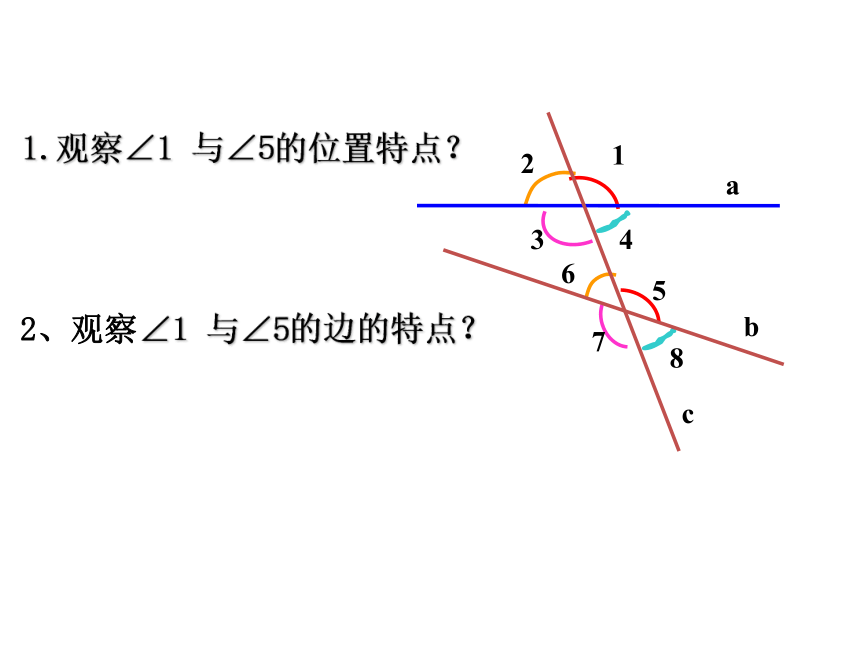
1.观察∠1 与∠5的位置特点?
2、观察∠1 与∠5的边的特点?
5
1
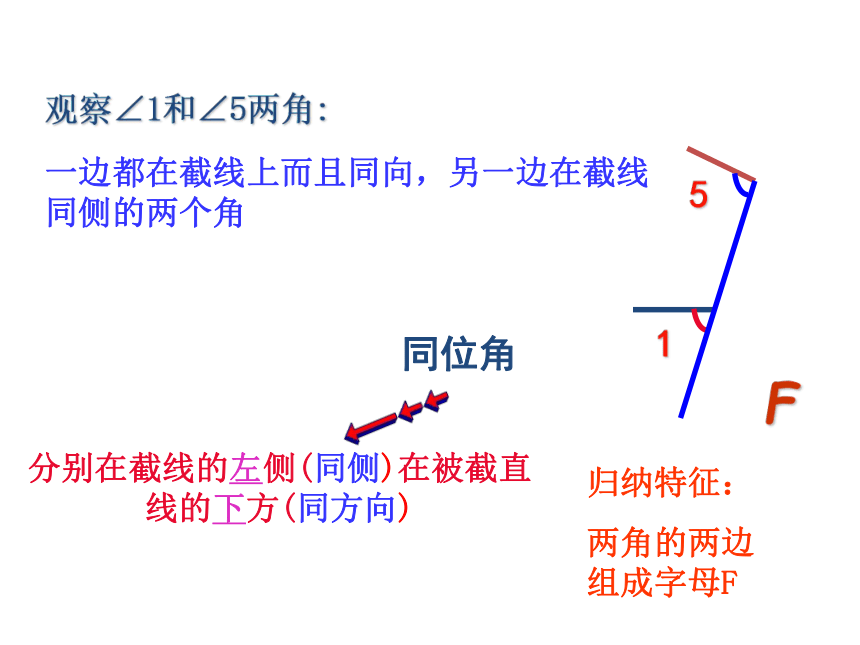
一边都在截线上而且同向,另一边在截线同侧的两个角
同位角
观察∠1和∠5两角:
分别在截线的左侧(同侧)在被截直线的下方(同方向)
归纳特征:
两角的两边组成字母F
F
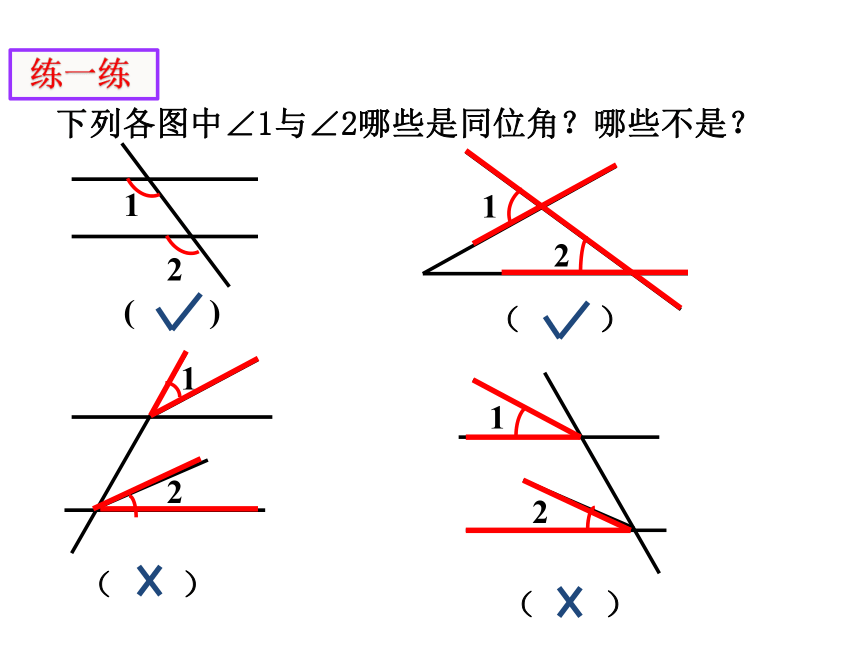
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
1
5
2
6
3
7
4
8
a
b
c
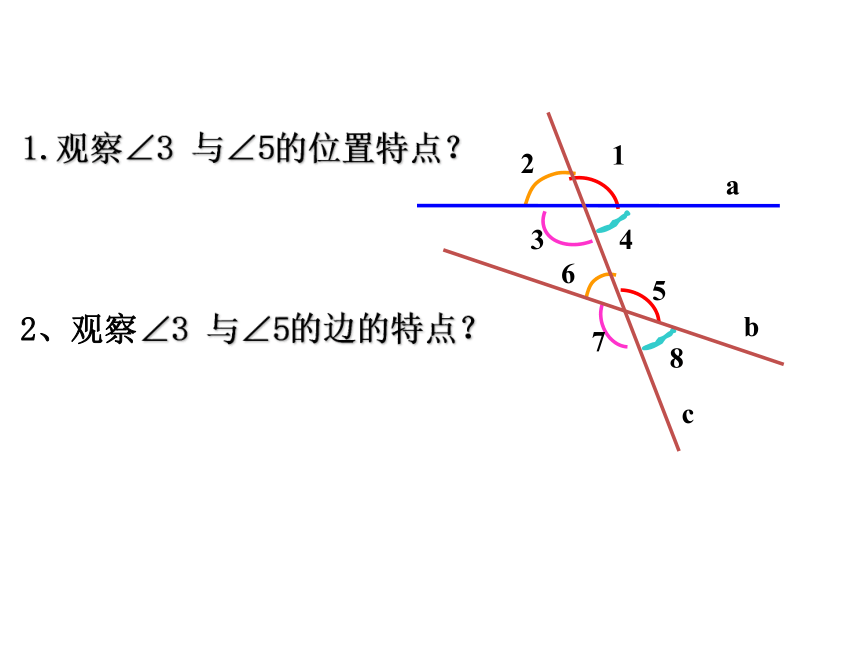
1.观察∠3 与∠5的位置特点?
2、观察∠3 与∠5的边的特点?
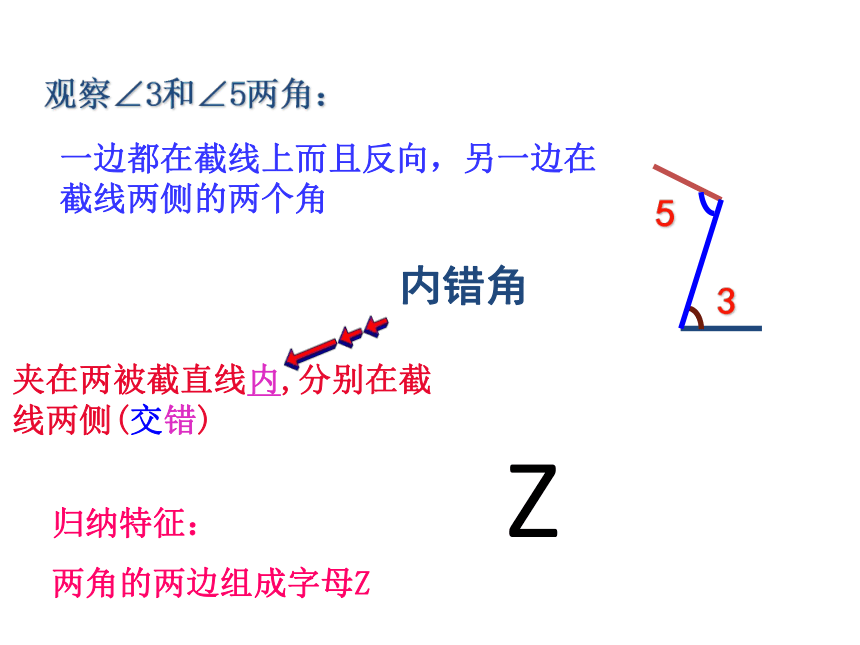
一边都在截线上而且反向,另一边在截线两侧的两个角
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线内,分别在截线两侧(交错)
Z
归纳特征:
两角的两边组成字母Z
1、如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B.内错角 C. 对顶角 D.同旁内角
2.如图,下列说法正确的是 ( )
A.∠1和∠4是同位角
B.∠1和∠4是内错角
C.∠1和∠A是内错角
D.∠3和∠4是同位角
B
A
1
5
2
6
3
7
4
8
a
b
c
1.观察∠4 与∠5的位置特点?
2、观察∠4 与∠5的边的特点?
一边都在截线上而且反向,另一边在截线同旁的两个角
同旁内角
5
4
观察∠4和∠5:
在截线同旁,夹在两被截直线内
归纳特征:两角的两边组成字母U
U
F
1
3
7
5
2
8
6
D
C
A
B
E
4
7
2
∠ 与 ∠ 是内错角;
4
5
∠ 与 ∠ 是内错角;
∠2 与 ∠5 是 角;
∠7 与 ∠4 是 角;
同旁内
同旁内
如图
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间(交错)
同侧
同旁
两旁
同旁
F (或倒置)
Z (或反置)
U
要点梳理
F
1
3
7
5
2
8
6
D
C
A
B
E
4
4
1
2
3
A
E
D
B
C
例1 如图,直线DE、BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4各是什么位置关系的角?
解:
∠1和∠2是内错角,∠1和∠3是同旁内角,
∠1和∠4是同位角.
例题讲解
解:如果∠1=∠4, 由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为 ∠3和∠4互补,即∠3 +∠4=180°,
又因为∠1=∠4,所以∠3 +∠1=180°,
即∠3和∠1互补.
(2)如果∠1=∠4,那∠1和∠2相等吗? ∠1和∠3互补吗?为什么?
4
1
2
3
A
E
D
B
C
例2、如图,直线a,b被直线c所截,已知∠1=∠5,那么∠3与∠7的关系如何 请说明理由.
解:∠3=∠7.
因为∠1=∠3,∠5=∠7(对顶角相等),
又 因为∠1=∠5(已知),
所以∠3=∠ 7(等量代换).
1、根据图形按要求填空:
(1)∠1与∠2是直线 和 被直线 所截得的 .
(2)∠1与∠3是直线 和 被直线 所截得的 .
(3)∠3与∠4是直线 和 被直线 所截得的 .
(4)∠4与∠5是直线 和 被直线 所截而得的 .
A
B
C
D
E
F
1
3
5
2
4
AB
DE
BC
同位角
随堂练习
AB
DE
BC
内错角
BC
EF
DE
内错角
BC
EF
DE
同旁内角
2、看图填空
(1)若ED,BF被AB所截,则∠1与___是同位角。
(2)若ED,BC被AF所截,则∠3与___是内错角。
(3)∠2与∠AFB是AB和AF被___所截构成的_____ 角。
∠2
∠4
BC
同旁内
拓展延伸
1、如图,三角形ABC中共有________对同旁内角,四 边形ABCD中共有_______对同旁内角,五边形ABCDE中共有________对同旁内角.
5
3
4
2、如图,在平面中画一条直线,使得与∠A成同旁内角的角有3个,你 能画出一条直线, 使得与∠A成同旁内角的角最多吗 最多有几个
解:如图(1),与∠A成同旁内角的角都有3个.
如图(2),与∠A成同旁内角的角最多,最多有4个.
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间(交错)
同侧
同旁
两旁
同旁
F (或倒置)
Z (或反置)
U
课堂小结
5.1.3 同位角 内错角 同旁内角
1.平面上两条直线有哪两种位置关系
(平行和相交)
2.两条直线相交有几个角
(4个)
3.两条直线与第三条直线相交呢?
(8个)
复习引入
观察图片,除了我们所学的两条直线相交外,有没有更多的直线相交呢?
画一画:如果三条直线相交,位置有哪几种呢?
A
C
B
D
E
F
7
1
2
3
4
5
6
8
如图:怎样描述这三条直线的位置关系?
直线AB、CD被直线EF所截
截线
探究新知
1
5
2
6
3
7
4
8
a
b
c
1.观察∠1 与∠5的位置特点?
2、观察∠1 与∠5的边的特点?
5
1
一边都在截线上而且同向,另一边在截线同侧的两个角
同位角
观察∠1和∠5两角:
分别在截线的左侧(同侧)在被截直线的下方(同方向)
归纳特征:
两角的两边组成字母F
F
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
1
5
2
6
3
7
4
8
a
b
c
1.观察∠3 与∠5的位置特点?
2、观察∠3 与∠5的边的特点?
一边都在截线上而且反向,另一边在截线两侧的两个角
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线内,分别在截线两侧(交错)
Z
归纳特征:
两角的两边组成字母Z
1、如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B.内错角 C. 对顶角 D.同旁内角
2.如图,下列说法正确的是 ( )
A.∠1和∠4是同位角
B.∠1和∠4是内错角
C.∠1和∠A是内错角
D.∠3和∠4是同位角
B
A
1
5
2
6
3
7
4
8
a
b
c
1.观察∠4 与∠5的位置特点?
2、观察∠4 与∠5的边的特点?
一边都在截线上而且反向,另一边在截线同旁的两个角
同旁内角
5
4
观察∠4和∠5:
在截线同旁,夹在两被截直线内
归纳特征:两角的两边组成字母U
U
F
1
3
7
5
2
8
6
D
C
A
B
E
4
7
2
∠ 与 ∠ 是内错角;
4
5
∠ 与 ∠ 是内错角;
∠2 与 ∠5 是 角;
∠7 与 ∠4 是 角;
同旁内
同旁内
如图
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间(交错)
同侧
同旁
两旁
同旁
F (或倒置)
Z (或反置)
U
要点梳理
F
1
3
7
5
2
8
6
D
C
A
B
E
4
4
1
2
3
A
E
D
B
C
例1 如图,直线DE、BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4各是什么位置关系的角?
解:
∠1和∠2是内错角,∠1和∠3是同旁内角,
∠1和∠4是同位角.
例题讲解
解:如果∠1=∠4, 由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为 ∠3和∠4互补,即∠3 +∠4=180°,
又因为∠1=∠4,所以∠3 +∠1=180°,
即∠3和∠1互补.
(2)如果∠1=∠4,那∠1和∠2相等吗? ∠1和∠3互补吗?为什么?
4
1
2
3
A
E
D
B
C
例2、如图,直线a,b被直线c所截,已知∠1=∠5,那么∠3与∠7的关系如何 请说明理由.
解:∠3=∠7.
因为∠1=∠3,∠5=∠7(对顶角相等),
又 因为∠1=∠5(已知),
所以∠3=∠ 7(等量代换).
1、根据图形按要求填空:
(1)∠1与∠2是直线 和 被直线 所截得的 .
(2)∠1与∠3是直线 和 被直线 所截得的 .
(3)∠3与∠4是直线 和 被直线 所截得的 .
(4)∠4与∠5是直线 和 被直线 所截而得的 .
A
B
C
D
E
F
1
3
5
2
4
AB
DE
BC
同位角
随堂练习
AB
DE
BC
内错角
BC
EF
DE
内错角
BC
EF
DE
同旁内角
2、看图填空
(1)若ED,BF被AB所截,则∠1与___是同位角。
(2)若ED,BC被AF所截,则∠3与___是内错角。
(3)∠2与∠AFB是AB和AF被___所截构成的_____ 角。
∠2
∠4
BC
同旁内
拓展延伸
1、如图,三角形ABC中共有________对同旁内角,四 边形ABCD中共有_______对同旁内角,五边形ABCDE中共有________对同旁内角.
5
3
4
2、如图,在平面中画一条直线,使得与∠A成同旁内角的角有3个,你 能画出一条直线, 使得与∠A成同旁内角的角最多吗 最多有几个
解:如图(1),与∠A成同旁内角的角都有3个.
如图(2),与∠A成同旁内角的角最多,最多有4个.
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间(交错)
同侧
同旁
两旁
同旁
F (或倒置)
Z (或反置)
U
课堂小结
