第五章平行与相交线【知识梳理】-七年级数学下学期(人教版)(47张ppt)
文档属性
| 名称 | 第五章平行与相交线【知识梳理】-七年级数学下学期(人教版)(47张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 00:00:00 | ||
图片预览







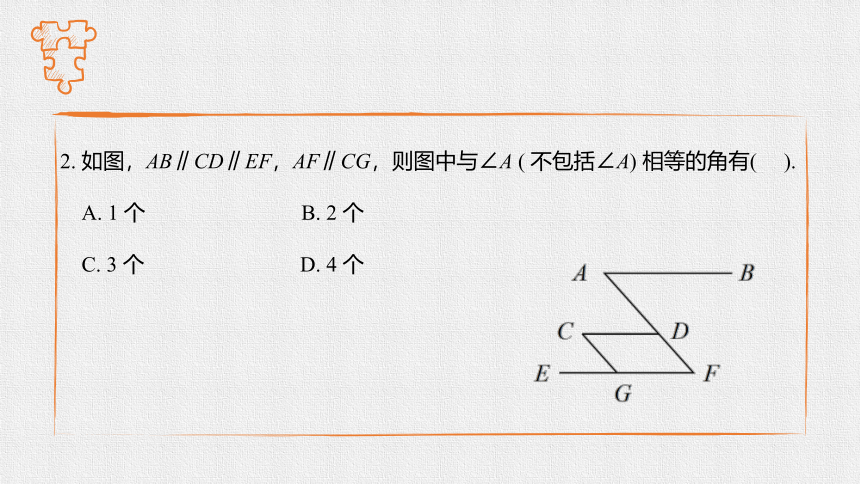
文档简介
(共47张PPT)
初中数学
相交线与平行线
目录
勤练重难点
平行线的判定和性质
平行线与垂线
平行线与角分线
PART 01
知识点回顾
你还记得吗?
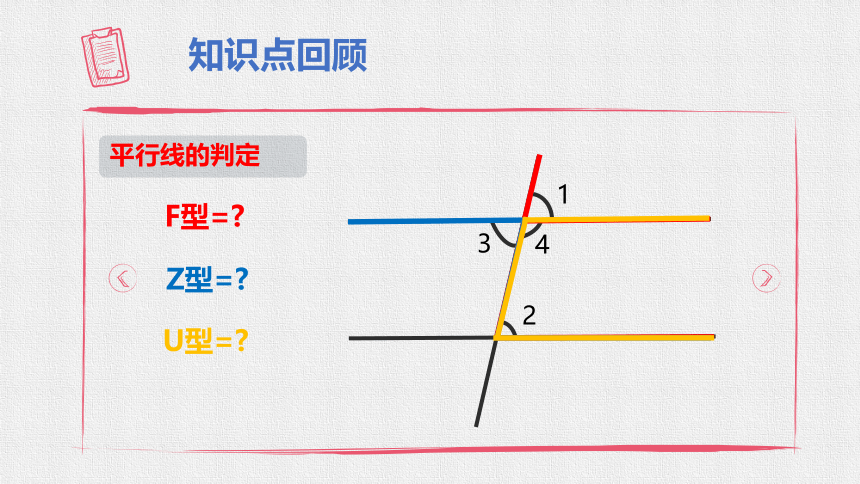
知识点回顾
平行线的判定
1
2
3
4
F型=
Z型=
U型=
PART 02
平行线的判定和性质
新知hold住
知识点1:平行线的性质
①两直线平行,同位角相等
②两直线平行,内错角相等
③两直线平行,同旁内角互补
平行在前,角在后
1
2
3
4
a
b
ab 1=2
ab 2=3
ab 24=180
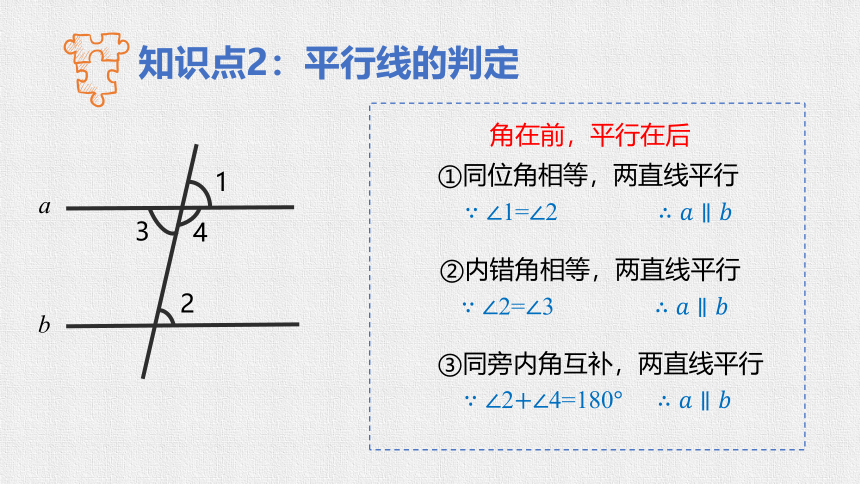
知识点2:平行线的判定
角在前,平行在后
1
2
3
4
a
b
①同位角相等,两直线平行
②内错角相等,两直线平行
③同旁内角互补,两直线平行
1=2
2=3
24=180
知识点3:常遇推理依据
①∵a//b
∴∠1=∠2
②∵∠1=∠2
∴a//b
(平行线的性质)
(平行线的判定)
③∵∠1=∠2 , ∠2=∠3
∴∠1=∠3
(等量代换)
④∵∠1=∠2
∴∠1± ∠3 =∠2± ∠3
(等式的性质)
⑤∵a⊥b
∴∠α=90°
(垂直定义)
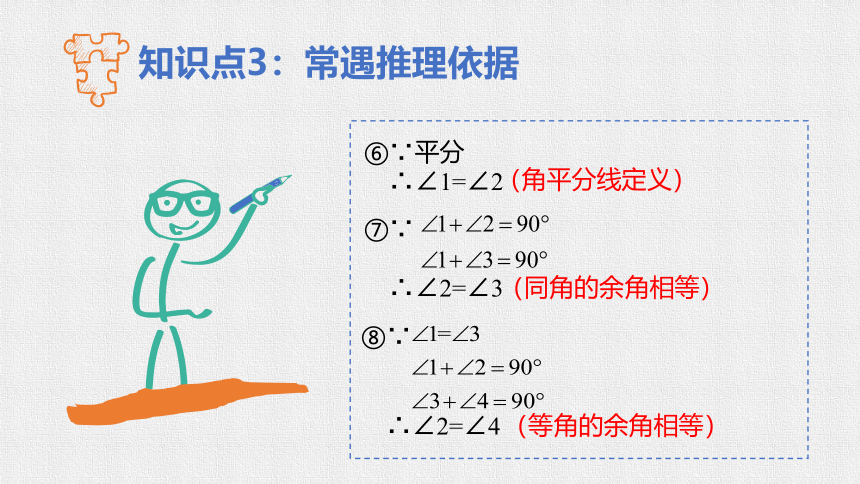
知识点3:常遇推理依据
⑥∵平分
∴∠1=∠2
⑦∵
∴∠2=∠3
(角平分线定义)
(同角的余角相等)
⑧∵
∴∠2=∠4
(等角的余角相等)
落实稳吸收
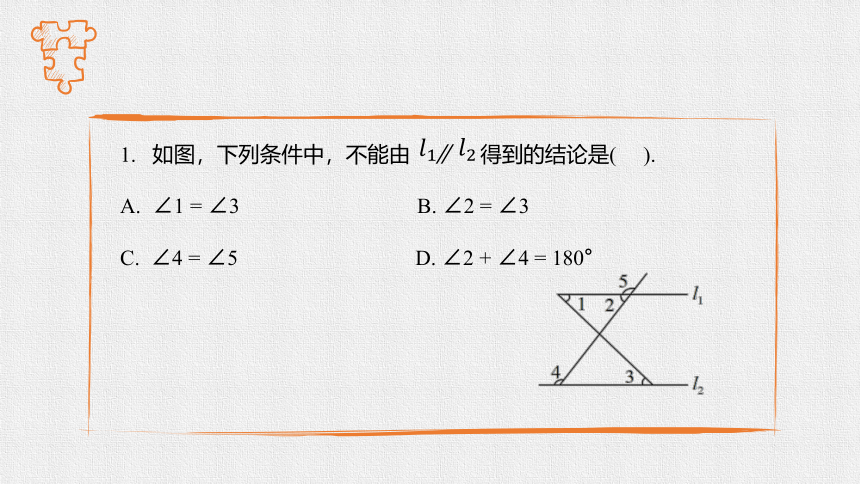
如图,下列条件中,不能由 ∥ 得到的结论是( ).
∠1 = ∠3 B. ∠2 = ∠3
C. ∠4 = ∠5 D. ∠2 + ∠4 = 180°
2. 如图,AB∥CD∥EF,AF∥CG,则图中与∠A ( 不包括∠A) 相等的角有( ).
A. 1 个 B. 2 个
C. 3 个 D. 4 个
3. 如图,已知∠1 = ∠3,CD∥EF,求证:∠1 = ∠4.
请根据条件进行推理,得出结论,并在括号内注明理由.
解:∵∠1 = ∠3 ( 已知),
又∵∠2 = ∠3 (_________________________),
∴∠1 = _______ (_________________________).
∴ _____∥______ (_________________________).
又∵ CD∥EF ( 已知),
∴ AB∥_______ (_______________________________).
∴∠1 = ∠4 (_________________________).
4. 如图,四边形ABCD 中,AD∥BC,点E 在BC 边上,点F 在AB 边上,且∠1 = ∠2.
(1) 求证:EF∥AC.
(2) 若CA 平分∠BCD,∠B = 50°,∠D = 120°,求∠BFE 的度数.
5. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角
相等.如图1,一束光线m 射到平面镜a 上,被a 反射后的光线为n,则入射光线m、反射光线n 与
平面镜a 所夹的锐角∠1 = ∠2.
(1) 利用这个规律人们制作了潜望镜,图2 是潜望镜工作原理示意图,AB、CD 是平行放置的两面平
面镜.已知光线经过平面镜反射时,有∠1 = ∠2,∠3 = ∠4,请解释进入潜望镜的光线m 为什么
和离开潜望镜的光线n 是平行的?
( 请把证明过程补充完整) 理由:
∵ AB∥CD ( 已知),
∴∠2 = ∠3 (___________________________).
∵∠1 = ∠2,∠3 = ∠4 ( 已知),
∴∠1 = ∠2 = ∠3 = ∠4 ( 等量代换).
∴ 180° - ∠1 - ∠2 = 180° - ∠3 - ∠4 ( 等量减等量,差相等).
即_________________ ( 等量代换).
∴ _________________ (______________________________).
(2) 显然,改变两面平面镜AB、CD 之间的位置关系,经过两次反射后,入射光线m 与反射光线n 之间的位置关系会随之改变,请你猜想:图3 中,当两平面镜AB、CD 的夹角∠ABC = _________° 时,仍可以使入射光线m 与反射光线n 平行但方向相反.
盲点排查清
1. 如图,AB∥CD,直线EF 分别交AB、CD 于点E、F,EH 平分∠BEF,若∠1 = 72°, ∠2 = ( ).
A. 54° B. 36°
C. 126° D. 74°
2. 光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,当∠1 = 45°,∠2 = 122° 时,∠3 和∠4 的度数分别是( ).
A. 58°;122° B. 45°;68°
C. 45°;58° D. 45°;45°
3. 完成下面的证明.
已知:如图,BC∥DE,BE、DF 分别是∠ABC、∠ADE 的平分线.
求证:∠1 = ∠2.
证明:∵ BC∥DE,
∴∠ABC = ∠ADE (_______________________).
∵ BE、DF 分别是∠ABC、∠ADE 的平分线,
∴∠3 = ∠ABC,∠4 = ∠ADE.
∴∠3 = ∠4.
∴ ______∥______ (________________________).
∴∠1 = ∠2 (________________________).
PART 03
平行线与垂线
难点来袭,小试牛刀!
1.垂线定义
两条直线相交所成的四个角中,有一个角是直角,就说这两条直线互相垂直。其中一条直线是另一条直线的垂线。
ab 1=90
2.垂线的性质
(1)在同一平面内,过一点(已知直线上或直线外)有且只有一条直线与已知直线垂直。
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。
3.点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
落实稳吸收
1. 将直尺和直角三角板按如图所示方式摆放,已知∠1 = 30°,则∠2 的度数是( ).
A. 30° B. 45°
C. 60° D. 65°
又∵ FH⊥AB,
∴∠FHB = 90° (____________).
∴∠CDB = ________°.
∴ CD⊥AB (____________).
2. 完成证明并写出推理根据:
已知,如图,∠1 = 132°,∠ACB = 48°,∠2 = ∠3,FH⊥AB 于H,
求证:CD⊥AB.
证明:∵∠1 = 132°,∠ACB = 48°,
∴∠1 + ∠ACB = 180°.
∴ DE∥BC.
∴∠2 = ∠DCB (_______________________).
又∵∠2 = ∠3,
∴∠3 = ∠DCB.
∴ HF∥DC (____________________________).
∴∠CDB = ∠FHB (_______________________).
4. 如图,BD⊥AC 于D,EF⊥AC 于F,DM∥BC,∠1 = ∠2.
求证:(1) GF∥BC.
(2)∠AMD = ∠AGF.
盲点排查清
1. 如图,直线AB∥CD,E 为直线AB 上一点,EH、EM 分别交直线CD 于点F、M,EH 平分∠AEM,MN⊥AB,垂足为点N,∠CFH = α.
(1) MN_______ME ( 填“ > ”或“ = ” 或“ < ”),理由是____________________________.
(2) ∠EMN = ______________ ( 用含α 的式子表示).
2. 如图,在△ABC 中,AD⊥BC 于D,G 是AC 上一点,GE⊥BC 于E,GE 的反向延长线与BA 的延长线交于点F,∠BAD = ∠CAD,求证:∠AGF = ∠F.
PART 04
平行线与角分线
新知hold住
知识点1:平行线+平分线
AD∥ BC,BD平分∠ABC
平行平分出等腰三角形
初二!
平行平分出三等角
∠ABD=∠CBD =∠ADB
知识点2:平行线+翻折
翻折产生对称相等
对应角相等
对应边相等
必须补全图形!
落实稳吸收
1. 如图,AB∥CD,直线PQ 分别交CD、AB 于点E、F,EG 是∠FED 的平分线,交AB 于点G.若∠QED = 40°,那么∠EGB = ___________.
2. 把一张长方形纸条按图中那样折叠后,若得到∠AOB' = 70°,则∠B'OG = ___________.
3. 把一张对边互相平行的纸条折成如图所示的样子,EF 是折痕,若∠EFB = 32°,则下列结论中正确的有( ) 个.
①∠C'EF = 32°;②∠AEC = 148°;③∠BGE = 64°;④∠BFD = 116°
A. 1 B. 2 C. 3 D. 4
盲点排查清
1. 如图,AB∥CD,直线EF 分别交直线AB、CD 于点E、F,FG 平分∠CFE 交AB 于点G,若∠BEF = 70°,则∠AGF = ______.
2. 如图1,ABCD 是长方形纸带(AD∥BC),∠DEF = 19°,将纸带沿EF 折叠成图2,再沿BF 折叠成图3,则图3 中的∠CFE 的度数是_____________.
3. 如图,AB∥DE,CM 平分∠BCE,CN⊥CM,求证:∠B = 2∠DCN.
勤练重难点
终极挑战!
PART 05
1. 如图,直线AB、CD 被直线EF 所截,交点分别为点E、F.若AB∥CD,下列结论正确的是( ).
A. ∠2 = ∠3 B. ∠2 = ∠4
C. ∠1 = ∠5 D. ∠3 + ∠AEF = 180°
2. 如图,AB∥CD,∠CDE = 140°,则∠A 的度数为_______.
3. 如图,△ABC 中,DE∥BC,DE 分别与AB、AC 交于点D、E,且∠1 = ∠B.
求证:∠A + ∠AEF = 180°.
下周见啦~
初中数学
相交线与平行线
目录
勤练重难点
平行线的判定和性质
平行线与垂线
平行线与角分线
PART 01
知识点回顾
你还记得吗?
知识点回顾
平行线的判定
1
2
3
4
F型=
Z型=
U型=
PART 02
平行线的判定和性质
新知hold住
知识点1:平行线的性质
①两直线平行,同位角相等
②两直线平行,内错角相等
③两直线平行,同旁内角互补
平行在前,角在后
1
2
3
4
a
b
ab 1=2
ab 2=3
ab 24=180
知识点2:平行线的判定
角在前,平行在后
1
2
3
4
a
b
①同位角相等,两直线平行
②内错角相等,两直线平行
③同旁内角互补,两直线平行
1=2
2=3
24=180
知识点3:常遇推理依据
①∵a//b
∴∠1=∠2
②∵∠1=∠2
∴a//b
(平行线的性质)
(平行线的判定)
③∵∠1=∠2 , ∠2=∠3
∴∠1=∠3
(等量代换)
④∵∠1=∠2
∴∠1± ∠3 =∠2± ∠3
(等式的性质)
⑤∵a⊥b
∴∠α=90°
(垂直定义)
知识点3:常遇推理依据
⑥∵平分
∴∠1=∠2
⑦∵
∴∠2=∠3
(角平分线定义)
(同角的余角相等)
⑧∵
∴∠2=∠4
(等角的余角相等)
落实稳吸收
如图,下列条件中,不能由 ∥ 得到的结论是( ).
∠1 = ∠3 B. ∠2 = ∠3
C. ∠4 = ∠5 D. ∠2 + ∠4 = 180°
2. 如图,AB∥CD∥EF,AF∥CG,则图中与∠A ( 不包括∠A) 相等的角有( ).
A. 1 个 B. 2 个
C. 3 个 D. 4 个
3. 如图,已知∠1 = ∠3,CD∥EF,求证:∠1 = ∠4.
请根据条件进行推理,得出结论,并在括号内注明理由.
解:∵∠1 = ∠3 ( 已知),
又∵∠2 = ∠3 (_________________________),
∴∠1 = _______ (_________________________).
∴ _____∥______ (_________________________).
又∵ CD∥EF ( 已知),
∴ AB∥_______ (_______________________________).
∴∠1 = ∠4 (_________________________).
4. 如图,四边形ABCD 中,AD∥BC,点E 在BC 边上,点F 在AB 边上,且∠1 = ∠2.
(1) 求证:EF∥AC.
(2) 若CA 平分∠BCD,∠B = 50°,∠D = 120°,求∠BFE 的度数.
5. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角
相等.如图1,一束光线m 射到平面镜a 上,被a 反射后的光线为n,则入射光线m、反射光线n 与
平面镜a 所夹的锐角∠1 = ∠2.
(1) 利用这个规律人们制作了潜望镜,图2 是潜望镜工作原理示意图,AB、CD 是平行放置的两面平
面镜.已知光线经过平面镜反射时,有∠1 = ∠2,∠3 = ∠4,请解释进入潜望镜的光线m 为什么
和离开潜望镜的光线n 是平行的?
( 请把证明过程补充完整) 理由:
∵ AB∥CD ( 已知),
∴∠2 = ∠3 (___________________________).
∵∠1 = ∠2,∠3 = ∠4 ( 已知),
∴∠1 = ∠2 = ∠3 = ∠4 ( 等量代换).
∴ 180° - ∠1 - ∠2 = 180° - ∠3 - ∠4 ( 等量减等量,差相等).
即_________________ ( 等量代换).
∴ _________________ (______________________________).
(2) 显然,改变两面平面镜AB、CD 之间的位置关系,经过两次反射后,入射光线m 与反射光线n 之间的位置关系会随之改变,请你猜想:图3 中,当两平面镜AB、CD 的夹角∠ABC = _________° 时,仍可以使入射光线m 与反射光线n 平行但方向相反.
盲点排查清
1. 如图,AB∥CD,直线EF 分别交AB、CD 于点E、F,EH 平分∠BEF,若∠1 = 72°, ∠2 = ( ).
A. 54° B. 36°
C. 126° D. 74°
2. 光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,当∠1 = 45°,∠2 = 122° 时,∠3 和∠4 的度数分别是( ).
A. 58°;122° B. 45°;68°
C. 45°;58° D. 45°;45°
3. 完成下面的证明.
已知:如图,BC∥DE,BE、DF 分别是∠ABC、∠ADE 的平分线.
求证:∠1 = ∠2.
证明:∵ BC∥DE,
∴∠ABC = ∠ADE (_______________________).
∵ BE、DF 分别是∠ABC、∠ADE 的平分线,
∴∠3 = ∠ABC,∠4 = ∠ADE.
∴∠3 = ∠4.
∴ ______∥______ (________________________).
∴∠1 = ∠2 (________________________).
PART 03
平行线与垂线
难点来袭,小试牛刀!
1.垂线定义
两条直线相交所成的四个角中,有一个角是直角,就说这两条直线互相垂直。其中一条直线是另一条直线的垂线。
ab 1=90
2.垂线的性质
(1)在同一平面内,过一点(已知直线上或直线外)有且只有一条直线与已知直线垂直。
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。
3.点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
落实稳吸收
1. 将直尺和直角三角板按如图所示方式摆放,已知∠1 = 30°,则∠2 的度数是( ).
A. 30° B. 45°
C. 60° D. 65°
又∵ FH⊥AB,
∴∠FHB = 90° (____________).
∴∠CDB = ________°.
∴ CD⊥AB (____________).
2. 完成证明并写出推理根据:
已知,如图,∠1 = 132°,∠ACB = 48°,∠2 = ∠3,FH⊥AB 于H,
求证:CD⊥AB.
证明:∵∠1 = 132°,∠ACB = 48°,
∴∠1 + ∠ACB = 180°.
∴ DE∥BC.
∴∠2 = ∠DCB (_______________________).
又∵∠2 = ∠3,
∴∠3 = ∠DCB.
∴ HF∥DC (____________________________).
∴∠CDB = ∠FHB (_______________________).
4. 如图,BD⊥AC 于D,EF⊥AC 于F,DM∥BC,∠1 = ∠2.
求证:(1) GF∥BC.
(2)∠AMD = ∠AGF.
盲点排查清
1. 如图,直线AB∥CD,E 为直线AB 上一点,EH、EM 分别交直线CD 于点F、M,EH 平分∠AEM,MN⊥AB,垂足为点N,∠CFH = α.
(1) MN_______ME ( 填“ > ”或“ = ” 或“ < ”),理由是____________________________.
(2) ∠EMN = ______________ ( 用含α 的式子表示).
2. 如图,在△ABC 中,AD⊥BC 于D,G 是AC 上一点,GE⊥BC 于E,GE 的反向延长线与BA 的延长线交于点F,∠BAD = ∠CAD,求证:∠AGF = ∠F.
PART 04
平行线与角分线
新知hold住
知识点1:平行线+平分线
AD∥ BC,BD平分∠ABC
平行平分出等腰三角形
初二!
平行平分出三等角
∠ABD=∠CBD =∠ADB
知识点2:平行线+翻折
翻折产生对称相等
对应角相等
对应边相等
必须补全图形!
落实稳吸收
1. 如图,AB∥CD,直线PQ 分别交CD、AB 于点E、F,EG 是∠FED 的平分线,交AB 于点G.若∠QED = 40°,那么∠EGB = ___________.
2. 把一张长方形纸条按图中那样折叠后,若得到∠AOB' = 70°,则∠B'OG = ___________.
3. 把一张对边互相平行的纸条折成如图所示的样子,EF 是折痕,若∠EFB = 32°,则下列结论中正确的有( ) 个.
①∠C'EF = 32°;②∠AEC = 148°;③∠BGE = 64°;④∠BFD = 116°
A. 1 B. 2 C. 3 D. 4
盲点排查清
1. 如图,AB∥CD,直线EF 分别交直线AB、CD 于点E、F,FG 平分∠CFE 交AB 于点G,若∠BEF = 70°,则∠AGF = ______.
2. 如图1,ABCD 是长方形纸带(AD∥BC),∠DEF = 19°,将纸带沿EF 折叠成图2,再沿BF 折叠成图3,则图3 中的∠CFE 的度数是_____________.
3. 如图,AB∥DE,CM 平分∠BCE,CN⊥CM,求证:∠B = 2∠DCN.
勤练重难点
终极挑战!
PART 05
1. 如图,直线AB、CD 被直线EF 所截,交点分别为点E、F.若AB∥CD,下列结论正确的是( ).
A. ∠2 = ∠3 B. ∠2 = ∠4
C. ∠1 = ∠5 D. ∠3 + ∠AEF = 180°
2. 如图,AB∥CD,∠CDE = 140°,则∠A 的度数为_______.
3. 如图,△ABC 中,DE∥BC,DE 分别与AB、AC 交于点D、E,且∠1 = ∠B.
求证:∠A + ∠AEF = 180°.
下周见啦~
