人教版九年级上册21.2.4 一元二次方程的根与系数的关系课件(共18张PPT)
文档属性
| 名称 | 人教版九年级上册21.2.4 一元二次方程的根与系数的关系课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 00:00:00 | ||
图片预览



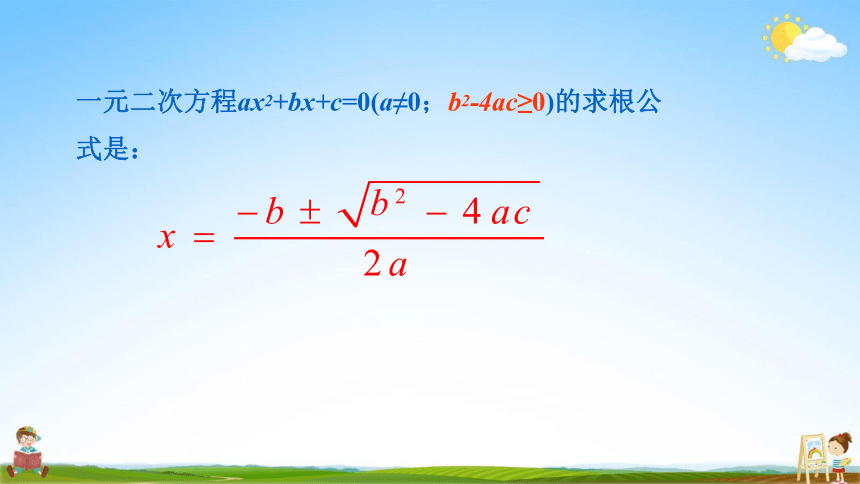



文档简介
(共18张PPT)
第二十一章 一元二次方程
21.2.4 根的判别式
人教版 数学 九年级 上册
用公式法求下列方程的根:
4
1
2)
3) x 2 x 1 0.
x 1 0;
x 2
1)2 x 2 x 2 0;
用公式法解一元 二次方程的一般步 骤:
4)利用求根公式 计算方程的根
2a
b 2
4ac
b
x
把方程化为一般形式
确定a、b、c的值
计算b2-4ac ,并判断 其值与0的关系
4 ac 0
b 2
一、知识回顾
b 2
2 a
b 4 a c
x
一元二次方程ax2+bx+c=0(a≠0)的求根公式是:
b 2
2 a
b 4 a c
x
一元二次方程ax2+bx+c=0(a≠0;b2-4ac≥0)的求根公 式是:
x 2
a a
b x c 0
x 2
a
b x c
b b
c
b
x 2
2
2
x
a
a 2 a
a 2 a
b
b 2
4 a 2
4 a c
2
x 2 a
配方 法
二、导入新课
如何把一元二次方程ax2+bx+c=0(a≠0)写成(x+h)2=k的形式?
a x 2 b x c 0
b 2
b
4 a 2
2
( a 0 )
x 2 a
4 a c
当 b 2
4 ac > 0 时,方 程的右边是一个正数,方 程有两个不
b 2 b 2
相等的实数根: x1
2 a
2 a
b 4 ac b 4 ac
; x2 ;
当 b 2
4 ac = 0
时, 方程的右边是
0 , 方程有两个相等的
;
b
2 a
实数根:
当 b 2
x1 x 2
4 ac < 0
时, 方程的右边是一个负数, 因为在实
数范围内, 负数没有平方根 .所 以, 方程没有实数根.
b 2
4 ac
思考:究竟是谁决定了一元二次方程根的情况
a 0, 4a 2 0
b2
4ac
反过来,对于方程ax2+bx+c=0(a≠0),
如果方程有两个不相等的实数根b2-4ac>0;
如果方程有两个相等的实数根b2-4ac=0; 如果方程没有实数根b2-4ac<0;
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0) 的根的判别式,用符号“△”来表示.
即一元二次方程ax2 bx c 0 a 0 ,
反之,
当方程有两个不相等的实数根时, 0; 当方程有两个相等的实数根时, 0; 当方程没有实数根时, 0.
当 0 时,方程有两个不相等的实数根;
当 0时,方程有两个相等的实数根;
当 0 时,方程没有实数根.
1:按要求完成下列表格:
Δ的值
让我们一起学习例题
根的情 况
有两个相等的实 数根
没有实数根
有两个不相等的 实数根
方程
判别式
与根
2 x 2 3 x 1 0
2 y 2 2 4 y
2 ( x 2 1) x 0
15 0
17 0
0 0
三、新课讲解
让我们一起 学习例题
一 般 步 骤:
1、化为一般式,确定a、b、c的值.
2、计算 的值,确定 的符号.
3、判别根的情况,得出结论.
2 : 不解方程,判别方程4y2+1=4y的根的情况.
解:4y2-4y+1=0
∵a=4,b=-4,c=1
∵△= (-4)2 -4×4×1=0
所以,方程两个相等的实数根。
你会了吗?来练一下吧! 我相信你肯定行!
不解方程,判别下列方程的根的情况:
(1) 1 x 2 3 x 8;
4
( 2 ) 5 t 2 1 7 t 0 .
eg3:不解方程,判别关于x的方程 的根的情况.
解: 2 2k 2 4 1 k 2
方程有两个实数根.
x2 2
2kx k 2 0
8k 2 4k 2 4k 2
k 2 0, 4k 2 0,即 0,
∵
分析:
a 1 b 2 2k
c k 2
ax 1 0 a 0
不解方程,判别关于x的方程 a2 x2 的根的情况.
解: ( a)2 4a2 ( 1) 5a2 ,且a 0
5a2 0,即 0
所以,原方程有两个不相等的实数根。
今天的收获:
我学会了……
我掌握了……
我体会到了……
四、课堂小结与反思
五、课堂检测:
1.不解方程,判断下x的方程的根的情况。
1)x2-2ax-2=0
2)ax2-bx-2=0(a≠0)
2.求证:方程 (m2+1)x2-2mx+( m2+1) =0没有实数根.
(1) 解 : 1 x 2 3 x 8 0
4
a 1 , b 3, c 8 4
( 3) 2 4 1 ( 8 )
4
17 0
所以,方程有两个不相等的实 数根
( 2 ) 解: 5 t 2 7 t 5 0
a 5 , b 7 , c 5
( 7 ) 2 4 5 5
51 0
所以,方程无实数根
看看你做的对不对?
3.已知关于x的方程x2-(2k+1)x+k2+1=0有两个不相等的实数根, 试确定的取值。
4.求证:关于x的方程k2x2-2kx-(k2-1)=0有实数根。
谢谢观看
Thank You
第二十一章 一元二次方程
21.2.4 根的判别式
人教版 数学 九年级 上册
用公式法求下列方程的根:
4
1
2)
3) x 2 x 1 0.
x 1 0;
x 2
1)2 x 2 x 2 0;
用公式法解一元 二次方程的一般步 骤:
4)利用求根公式 计算方程的根
2a
b 2
4ac
b
x
把方程化为一般形式
确定a、b、c的值
计算b2-4ac ,并判断 其值与0的关系
4 ac 0
b 2
一、知识回顾
b 2
2 a
b 4 a c
x
一元二次方程ax2+bx+c=0(a≠0)的求根公式是:
b 2
2 a
b 4 a c
x
一元二次方程ax2+bx+c=0(a≠0;b2-4ac≥0)的求根公 式是:
x 2
a a
b x c 0
x 2
a
b x c
b b
c
b
x 2
2
2
x
a
a 2 a
a 2 a
b
b 2
4 a 2
4 a c
2
x 2 a
配方 法
二、导入新课
如何把一元二次方程ax2+bx+c=0(a≠0)写成(x+h)2=k的形式?
a x 2 b x c 0
b 2
b
4 a 2
2
( a 0 )
x 2 a
4 a c
当 b 2
4 ac > 0 时,方 程的右边是一个正数,方 程有两个不
b 2 b 2
相等的实数根: x1
2 a
2 a
b 4 ac b 4 ac
; x2 ;
当 b 2
4 ac = 0
时, 方程的右边是
0 , 方程有两个相等的
;
b
2 a
实数根:
当 b 2
x1 x 2
4 ac < 0
时, 方程的右边是一个负数, 因为在实
数范围内, 负数没有平方根 .所 以, 方程没有实数根.
b 2
4 ac
思考:究竟是谁决定了一元二次方程根的情况
a 0, 4a 2 0
b2
4ac
反过来,对于方程ax2+bx+c=0(a≠0),
如果方程有两个不相等的实数根b2-4ac>0;
如果方程有两个相等的实数根b2-4ac=0; 如果方程没有实数根b2-4ac<0;
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0) 的根的判别式,用符号“△”来表示.
即一元二次方程ax2 bx c 0 a 0 ,
反之,
当方程有两个不相等的实数根时, 0; 当方程有两个相等的实数根时, 0; 当方程没有实数根时, 0.
当 0 时,方程有两个不相等的实数根;
当 0时,方程有两个相等的实数根;
当 0 时,方程没有实数根.
1:按要求完成下列表格:
Δ的值
让我们一起学习例题
根的情 况
有两个相等的实 数根
没有实数根
有两个不相等的 实数根
方程
判别式
与根
2 x 2 3 x 1 0
2 y 2 2 4 y
2 ( x 2 1) x 0
15 0
17 0
0 0
三、新课讲解
让我们一起 学习例题
一 般 步 骤:
1、化为一般式,确定a、b、c的值.
2、计算 的值,确定 的符号.
3、判别根的情况,得出结论.
2 : 不解方程,判别方程4y2+1=4y的根的情况.
解:4y2-4y+1=0
∵a=4,b=-4,c=1
∵△= (-4)2 -4×4×1=0
所以,方程两个相等的实数根。
你会了吗?来练一下吧! 我相信你肯定行!
不解方程,判别下列方程的根的情况:
(1) 1 x 2 3 x 8;
4
( 2 ) 5 t 2 1 7 t 0 .
eg3:不解方程,判别关于x的方程 的根的情况.
解: 2 2k 2 4 1 k 2
方程有两个实数根.
x2 2
2kx k 2 0
8k 2 4k 2 4k 2
k 2 0, 4k 2 0,即 0,
∵
分析:
a 1 b 2 2k
c k 2
ax 1 0 a 0
不解方程,判别关于x的方程 a2 x2 的根的情况.
解: ( a)2 4a2 ( 1) 5a2 ,且a 0
5a2 0,即 0
所以,原方程有两个不相等的实数根。
今天的收获:
我学会了……
我掌握了……
我体会到了……
四、课堂小结与反思
五、课堂检测:
1.不解方程,判断下x的方程的根的情况。
1)x2-2ax-2=0
2)ax2-bx-2=0(a≠0)
2.求证:方程 (m2+1)x2-2mx+( m2+1) =0没有实数根.
(1) 解 : 1 x 2 3 x 8 0
4
a 1 , b 3, c 8 4
( 3) 2 4 1 ( 8 )
4
17 0
所以,方程有两个不相等的实 数根
( 2 ) 解: 5 t 2 7 t 5 0
a 5 , b 7 , c 5
( 7 ) 2 4 5 5
51 0
所以,方程无实数根
看看你做的对不对?
3.已知关于x的方程x2-(2k+1)x+k2+1=0有两个不相等的实数根, 试确定的取值。
4.求证:关于x的方程k2x2-2kx-(k2-1)=0有实数根。
谢谢观看
Thank You
同课章节目录
