人教版九年级上册21.2 解一元二次方程21.2.4 一元二次方程的根与系数的关系课件(共29张PPT)
文档属性
| 名称 | 人教版九年级上册21.2 解一元二次方程21.2.4 一元二次方程的根与系数的关系课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 11:24:46 | ||
图片预览





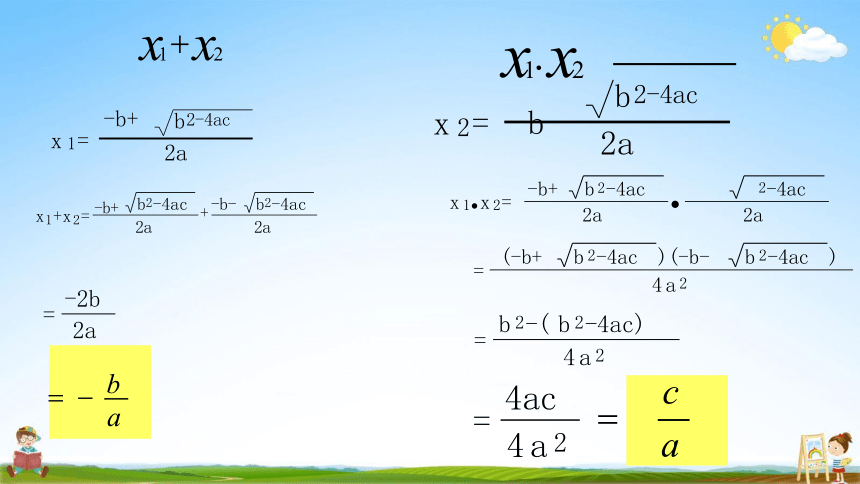


文档简介
(共29张PPT)
第二十一章 一元二次方程
21.2.5 根与系数关系
人教版 数学 九年级 上册
一元二次方程的解法
求根公式
一、知识回顾
1 2 1 2
2.会用根的判别式及根与系数关系解题.
a
x + x = - b , x · x =
a
c
二、目标展示
学习目标:
1.理解并掌握根与系数关系:
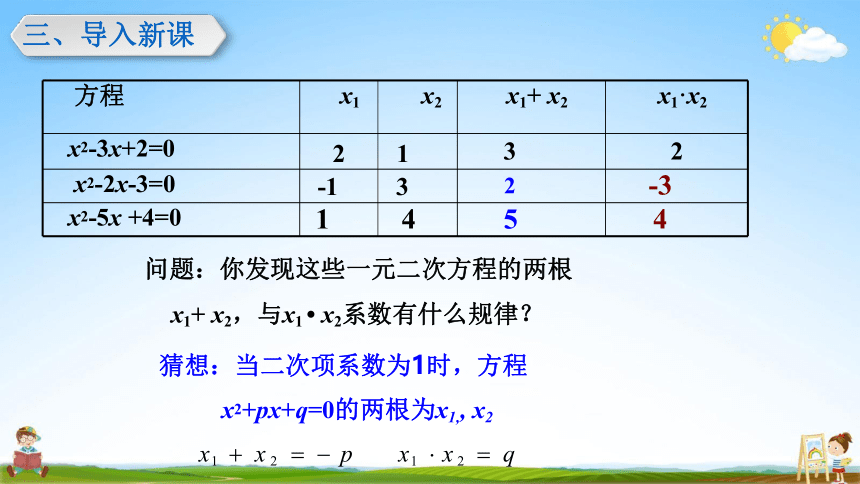
问题:你发现这些一元二次方程的两根
x1+ x2,与x1 x2系数有什么规律?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,, x2
x1 x 2 p x1 x 2 q
方程 x1 x2 x1+ x2 x1·x2
x2-3x+2=0 2 1 3 2
x2-2x-3=0 -1 3 2 -3
x2-5x +4=0 1 4 5 4
三、导入新课
x1+ x2,x1 x2与系数有什么规律
方 程 x 1 x 2 x 1 x 2 x 1 . x
2
9 x2 6 x 1 0 1 1 2 1
3 3 3 9
3 x2 4 x 1 0 2 7 2 7 4 1
3 3 3 3
3 x2 7 x 2 0 1 -2 7 2
3 3 3
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)
的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
a
b
x x
2
1
a
c
x x
2
1
4ac 0
b 2
探究新知:
1 2
x +x = -b+
b2-4ac
2a
+ -b-
b2-4ac
2a
-b+
x 1 =
b 2-4ac
2a
x 2 =
2a
=
-2b
2a
x 1 x 2 =
-b+ b 2 -4ac
2a
2 -4ac
2a
=
b 2 -4ac )
=
4ac
4 a 2
=
(-b+ b 2 -4ac )(-b-
4 a 2
b 2 -( b 2 -4ac)
4 a 2
x1 x2
b 2-4ac
x1.x2
-b-
a
b
a
c
, x1 ·x2=
b
那么x1 + x2= - a
a
任何一个一元二次方程的根与系数的关系:
(韦达定理)
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
c
注:能用根与系数的关系的前提条件为b2-4ac≥0
例1、不解方程,求下列方程两根的和与积.
(1) x 2 6 x 15 0
( 2 )3 x 2 7 x 9 0
(3)5 x 1 4 x 2
例题讲解:
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
a
注意“- ”不要漏写.
⑵在使用x1+x2= - b 时,
的两个根
,利用根与系数的关系,求下列各式的值.
例2、设 x1 , x2 是方程
2x2 4x 3 0
(1) x 2 x 2
1 2
(3)( x1 1)( x2 1)
1 2
1 2
(4) x 2 x
x x 2
x1 x 2
( 5 ) x 2
x1
2
1
) 2
( 6 )( x x
2
1
x x
(2) 1 1
关于两根几种常见的求值
1
4 . 1
x1 x 2
1)
x1 x 2
1)( x 2
x 1 x 2 ( x 1 x 2 ) 1
x 2 x1
x1 x 2
x1 x 2
5 .
1 2
x1 x 2
x 2
x 2
) 2
1 2 1 2
x1 x 2
( x x 2 x x
x 2
6 . x1
( x1 x 2 )
2
( x1 x 2 ) 4 x x
2
1 2
2
1
x 2
1 .x 2
2
1
) 2
( x x
2 .( x1 x 2 )
2
3 .( x1
( x1 x 2 )
2
2 x1 x 2
4 x1 x 2
例3、求一个一元二次方程,使它的两个根是2和3,且二
次项系数为1.
变式:且二次项系数为5
例4、已知关于x的方程x2-5x-2=0(1),且关于y的方程的两
根分别是关于方程(1)
的两根
的平方.
求关于y的方程.
的倒数.
的相反数.
比
都大2.
例5 、小明和小敏解同一个一元二次方程时, 小明看 错了一次项系数所求出的根为- 9 和- 1 ; 小敏看错了常
数项所求出的根是8 和2 。你知道原来的方程是什么吗?
1 . 甲、乙二人解同一个一元二次方程时, 甲看错了常数 项所求出的根为1 , 4 ; 乙看错了一次项系数所求出的根 是- 2 ,- 3 。则这个一元二次方程为
_____________________
x2-5x+6=0
课堂练习:
(还有其他解法吗?)
m=__-3__。
x2 mx 3 0
3、已知3是方程 x2-mx-3=0的一根,求m及另一根.
3
2、如果-1是方程的一个根,2x2-x+m=0则另一个根是__2__
例7、方程x2+px+q=0 的两根同为正数,求p、q的取值范围.
四、求方程中的待定系数
根,求m的取值范围.
解:由已知,
4m2 4m(m 1) 0
△=
1 2
m
m 1 0
x x
即
m>0 m-1<0
∴02mx m 1 0(m 0) 有一个正根,一个负
4、方程 mx 2
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0 X1+X2>0
两个负根
△≥0
X1X2>0 X1+X2<0
5、 已知方程 x2 kx k 2 0 的两个实数根是
x1, x2
2
1
4 求k的值。
x 2
且 x 2
注:能用根与系数的关系的前提条件为b2-4ac≥0
1、一元二次方程根与系数的关系?
a
c a
2
1
2
1
1 2
2
x , x x
则有 x b ; x . x
如果 ax bx C 0 ( a 0 )的两根分别是
注:能用根与系数的关系的前提条件为b2-4ac≥0
课堂小结与反思:
教材p16练习.
教材p17习题第7题
布置作业:
解法(一):设两数分别为x,y则:
x y 1
解得:
x=2 y=-1
{
或
{ x y 2
x=-1 y=2
{
解法(二):设两数分别为一个一元二次方程的两根则:
a2 a 2 0
求得
a1 2, a2 1
∴两数为2,-1
*已知两个数的和与积,求两数
已知两个数的和是1,积是-2,则两个数是
* 求未知系数的取值范围
*例题:已知关于x的方程9x2 +(m+7)x+m-3=0.
(1)求证:无论k取何值时,方程总有两不相等的实数根. (2)当k取何值时,方程的一根大于1,另一根小于1
分析:
(1)列出△的代数式,证其恒大于零 (2)(x1-1)(x2-1)<0
解:(1)∵△=(m+7)2-4(m-3)=(m+5)2+36>0
∴方程总有两个不相等的实数根
解得:
1
2
1 2
9
9
x
x
m 7
m 3
( x1 1)( x 2 1) 0
(2)由题意得: x x
2
m 1 3
当 时方程的一根大于1,另一根小于1
2
m 1 3
*1.当a取什么值时,关于未知数x的方程ax2+4x-1=0,只有正实数根
*2.已知:x1,x2是关于x的一元二次方程4x2+4(m-1)x+m2=0的两个 非零实根,问x1,x2能否同号 若能同号,请求出相应m的取值范围;若 不能同号,请说明理由.
3 b ) 0
***题9 在△ABC中a,b,c分别为∠A, ∠B,∠C
的对边,且c= 5 3 ,若关于x的方程
( 5 3 b ) x 2 2 ax ( 5
有两个相等的实数根,又方程
2 x 2 (10 sin A ) x 5 sin A 0
的两实数根的平方和为6,求△ABC的面积.
c
规定: sin A a
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵ (x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2=
1 2
, x x =
k 1 2
k 3 2
2 2
1 ) 2 3 1
4 k
∴ ( k
解得k1=9,k2= -3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
谢谢观看
Thank You
第二十一章 一元二次方程
21.2.5 根与系数关系
人教版 数学 九年级 上册
一元二次方程的解法
求根公式
一、知识回顾
1 2 1 2
2.会用根的判别式及根与系数关系解题.
a
x + x = - b , x · x =
a
c
二、目标展示
学习目标:
1.理解并掌握根与系数关系:
问题:你发现这些一元二次方程的两根
x1+ x2,与x1 x2系数有什么规律?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,, x2
x1 x 2 p x1 x 2 q
方程 x1 x2 x1+ x2 x1·x2
x2-3x+2=0 2 1 3 2
x2-2x-3=0 -1 3 2 -3
x2-5x +4=0 1 4 5 4
三、导入新课
x1+ x2,x1 x2与系数有什么规律
方 程 x 1 x 2 x 1 x 2 x 1 . x
2
9 x2 6 x 1 0 1 1 2 1
3 3 3 9
3 x2 4 x 1 0 2 7 2 7 4 1
3 3 3 3
3 x2 7 x 2 0 1 -2 7 2
3 3 3
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)
的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
a
b
x x
2
1
a
c
x x
2
1
4ac 0
b 2
探究新知:
1 2
x +x = -b+
b2-4ac
2a
+ -b-
b2-4ac
2a
-b+
x 1 =
b 2-4ac
2a
x 2 =
2a
=
-2b
2a
x 1 x 2 =
-b+ b 2 -4ac
2a
2 -4ac
2a
=
b 2 -4ac )
=
4ac
4 a 2
=
(-b+ b 2 -4ac )(-b-
4 a 2
b 2 -( b 2 -4ac)
4 a 2
x1 x2
b 2-4ac
x1.x2
-b-
a
b
a
c
, x1 ·x2=
b
那么x1 + x2= - a
a
任何一个一元二次方程的根与系数的关系:
(韦达定理)
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
c
注:能用根与系数的关系的前提条件为b2-4ac≥0
例1、不解方程,求下列方程两根的和与积.
(1) x 2 6 x 15 0
( 2 )3 x 2 7 x 9 0
(3)5 x 1 4 x 2
例题讲解:
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
a
注意“- ”不要漏写.
⑵在使用x1+x2= - b 时,
的两个根
,利用根与系数的关系,求下列各式的值.
例2、设 x1 , x2 是方程
2x2 4x 3 0
(1) x 2 x 2
1 2
(3)( x1 1)( x2 1)
1 2
1 2
(4) x 2 x
x x 2
x1 x 2
( 5 ) x 2
x1
2
1
) 2
( 6 )( x x
2
1
x x
(2) 1 1
关于两根几种常见的求值
1
4 . 1
x1 x 2
1)
x1 x 2
1)( x 2
x 1 x 2 ( x 1 x 2 ) 1
x 2 x1
x1 x 2
x1 x 2
5 .
1 2
x1 x 2
x 2
x 2
) 2
1 2 1 2
x1 x 2
( x x 2 x x
x 2
6 . x1
( x1 x 2 )
2
( x1 x 2 ) 4 x x
2
1 2
2
1
x 2
1 .x 2
2
1
) 2
( x x
2 .( x1 x 2 )
2
3 .( x1
( x1 x 2 )
2
2 x1 x 2
4 x1 x 2
例3、求一个一元二次方程,使它的两个根是2和3,且二
次项系数为1.
变式:且二次项系数为5
例4、已知关于x的方程x2-5x-2=0(1),且关于y的方程的两
根分别是关于方程(1)
的两根
的平方.
求关于y的方程.
的倒数.
的相反数.
比
都大2.
例5 、小明和小敏解同一个一元二次方程时, 小明看 错了一次项系数所求出的根为- 9 和- 1 ; 小敏看错了常
数项所求出的根是8 和2 。你知道原来的方程是什么吗?
1 . 甲、乙二人解同一个一元二次方程时, 甲看错了常数 项所求出的根为1 , 4 ; 乙看错了一次项系数所求出的根 是- 2 ,- 3 。则这个一元二次方程为
_____________________
x2-5x+6=0
课堂练习:
(还有其他解法吗?)
m=__-3__。
x2 mx 3 0
3、已知3是方程 x2-mx-3=0的一根,求m及另一根.
3
2、如果-1是方程的一个根,2x2-x+m=0则另一个根是__2__
例7、方程x2+px+q=0 的两根同为正数,求p、q的取值范围.
四、求方程中的待定系数
根,求m的取值范围.
解:由已知,
4m2 4m(m 1) 0
△=
1 2
m
m 1 0
x x
即
m>0 m-1<0
∴0
4、方程 mx 2
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0 X1+X2>0
两个负根
△≥0
X1X2>0 X1+X2<0
5、 已知方程 x2 kx k 2 0 的两个实数根是
x1, x2
2
1
4 求k的值。
x 2
且 x 2
注:能用根与系数的关系的前提条件为b2-4ac≥0
1、一元二次方程根与系数的关系?
a
c a
2
1
2
1
1 2
2
x , x x
则有 x b ; x . x
如果 ax bx C 0 ( a 0 )的两根分别是
注:能用根与系数的关系的前提条件为b2-4ac≥0
课堂小结与反思:
教材p16练习.
教材p17习题第7题
布置作业:
解法(一):设两数分别为x,y则:
x y 1
解得:
x=2 y=-1
{
或
{ x y 2
x=-1 y=2
{
解法(二):设两数分别为一个一元二次方程的两根则:
a2 a 2 0
求得
a1 2, a2 1
∴两数为2,-1
*已知两个数的和与积,求两数
已知两个数的和是1,积是-2,则两个数是
* 求未知系数的取值范围
*例题:已知关于x的方程9x2 +(m+7)x+m-3=0.
(1)求证:无论k取何值时,方程总有两不相等的实数根. (2)当k取何值时,方程的一根大于1,另一根小于1
分析:
(1)列出△的代数式,证其恒大于零 (2)(x1-1)(x2-1)<0
解:(1)∵△=(m+7)2-4(m-3)=(m+5)2+36>0
∴方程总有两个不相等的实数根
解得:
1
2
1 2
9
9
x
x
m 7
m 3
( x1 1)( x 2 1) 0
(2)由题意得: x x
2
m 1 3
当 时方程的一根大于1,另一根小于1
2
m 1 3
*1.当a取什么值时,关于未知数x的方程ax2+4x-1=0,只有正实数根
*2.已知:x1,x2是关于x的一元二次方程4x2+4(m-1)x+m2=0的两个 非零实根,问x1,x2能否同号 若能同号,请求出相应m的取值范围;若 不能同号,请说明理由.
3 b ) 0
***题9 在△ABC中a,b,c分别为∠A, ∠B,∠C
的对边,且c= 5 3 ,若关于x的方程
( 5 3 b ) x 2 2 ax ( 5
有两个相等的实数根,又方程
2 x 2 (10 sin A ) x 5 sin A 0
的两实数根的平方和为6,求△ABC的面积.
c
规定: sin A a
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵ (x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2=
1 2
, x x =
k 1 2
k 3 2
2 2
1 ) 2 3 1
4 k
∴ ( k
解得k1=9,k2= -3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
谢谢观看
Thank You
同课章节目录
