2021-2022学年高二数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质导学案
文档属性
| 名称 | 2021-2022学年高二数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质导学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 67.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 00:00:00 | ||
图片预览


文档简介
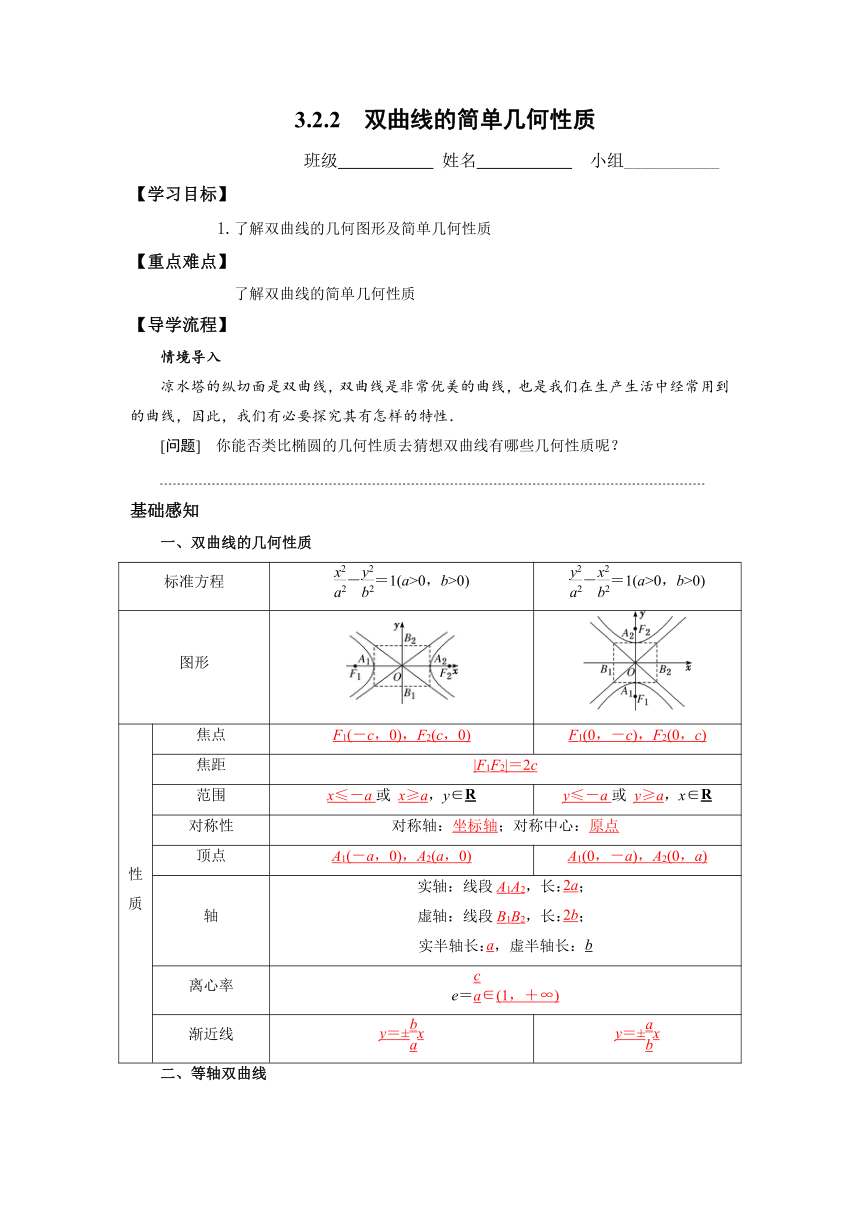
3.2.2 双曲线的简单几何性质
班级 姓名 小组___________
【学习目标】
1.了解双曲线的几何图形及简单几何性质
【重点难点】
了解双曲线的简单几何性质
【导学流程】
情境导入
凉水塔的纵切面是双曲线,双曲线是非常优美的曲线,也是我们在生产生活中经常用到的曲线,因此,我们有必要探究其有怎样的特性.
[问题] 你能否类比椭圆的几何性质去猜想双曲线有哪些几何性质呢?
基础感知
一、双曲线的几何性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
图形
性质 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 |F1F2|=2c
范围 x≤-a或 x≥a,y∈ y≤-a或 y≥a,x∈
对称性 对称轴:坐标轴;对称中心:原点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:; 虚轴:线段B1B2,长:; 实半轴长:,虚半轴长:
离心率 e=∈(1,+∞)
渐近线 y=±x y=±x
二、等轴双曲线
实轴和虚轴等长的双曲线叫做等轴双曲线,它的渐近线方程为y=±x.
合作与交流
1.椭圆与双曲线的离心率都是e,其范围一样吗?
提示:不一样,椭圆的离心率01.
2.若双曲线确定,则渐近线确定吗?反过来呢?
提示:当双曲线的方程确定后,其渐近线方程也就确定了;反过来,确定的渐近线却对应着无数条双曲线,如具有相同的渐近线y=±x的双曲线可设为-=λ(λ≠0,λ∈R),当λ>0时,焦点在x轴上,当λ<0时,焦点在y轴上.
3.判断正误.(正确的画“√”,错误的画“×”)
(1)共渐近线的双曲线的离心率相同.( × )
(2)双曲线-=1与-=1(a>0,b>0)的渐近线相同.(× )
(3)双曲线-=1的渐近线方程是3x±2y=0.( √ )
典例分析
例1. (链接教科书第124页练习1题)求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
[解] 双曲线的方程化为标准形式是-=1,
∴a2=9,b2=4,∴a=3,b=2,c=.
又双曲线的焦点在x轴上,∴顶点坐标为(-3,0),(3,0),
焦点坐标为(-,0),(,0),
实轴长2a=6,虚轴长2b=4,
离心率e==,渐近线方程为y=±x.
小结1.由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准形式是解决此类题的关键;
(2)由标准方程确定焦点位置,确定a,b的值;
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
[注意] 求性质时一定要注意焦点的位置.
例2. (链接教科书第124页练习2题)(1)以椭圆+=1的顶点为顶点,离心率为2的双曲线方程为( )
A.-=1 B.-=1 C.-=1或-=1 D.以上都不对
(2)过点(2,-2)且与-y2=1有相同渐近线的双曲线的标准方程为___-=1._____.
小结2.求双曲线的标准方程的方法与技巧
(1)一般情况下,求双曲线的标准方程关键是确定a,b的值和焦点所在的坐标轴,若给出双曲线的顶点坐标或焦点坐标,则焦点所在的坐标轴易得.再结合c2=a2+b2及e=列关于a,b的方程(组),解方程(组)可得标准方程;
(2)如果已知双曲线的渐近线方程为y=±x,那么此双曲线方程可设为-=λ(λ≠0).
例3. 如图所示,F1和F2分别是双曲线-=1(a>0,b>0)的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为__1+______.
小结3.求双曲线离心率的两种方法
(1)直接法:若已知a,c可直接利用e=求解,若已知a,b,可利用e= 求解;
(2)方程法:若无法求出a,b,c的具体值,但根据条件可确定a,b,c之间的关系,可通过b2=c2-a2,将关系式转化为关于a,c的齐次方程,借助于e=,转化为关于e的n次方程求解.
1.已知双曲线的实轴和虚轴等长,且过点(5,3),则双曲线方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析:选D 由题意知,所求双曲线是等轴双曲线,设其方程为x2-y2=λ(λ≠0),将点(5,3)代入方程,可得λ=52-32=16,所以双曲线方程为x2-y2=16,即-=1.
2.(2020·全国卷Ⅲ)设双曲线C:-=1(a>0,b>0)的一条渐近线为y=x,则C的离心率为________.
解析:由双曲线的一条渐近线为y=x可知,=,即b=a.在双曲线中,c2=a2+b2,所以c2=3a2,所以e==.
答案:
班级 姓名 小组___________
【学习目标】
1.了解双曲线的几何图形及简单几何性质
【重点难点】
了解双曲线的简单几何性质
【导学流程】
情境导入
凉水塔的纵切面是双曲线,双曲线是非常优美的曲线,也是我们在生产生活中经常用到的曲线,因此,我们有必要探究其有怎样的特性.
[问题] 你能否类比椭圆的几何性质去猜想双曲线有哪些几何性质呢?
基础感知
一、双曲线的几何性质
标准方程 -=1(a>0,b>0) -=1(a>0,b>0)
图形
性质 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 |F1F2|=2c
范围 x≤-a或 x≥a,y∈ y≤-a或 y≥a,x∈
对称性 对称轴:坐标轴;对称中心:原点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:; 虚轴:线段B1B2,长:; 实半轴长:,虚半轴长:
离心率 e=∈(1,+∞)
渐近线 y=±x y=±x
二、等轴双曲线
实轴和虚轴等长的双曲线叫做等轴双曲线,它的渐近线方程为y=±x.
合作与交流
1.椭圆与双曲线的离心率都是e,其范围一样吗?
提示:不一样,椭圆的离心率0
2.若双曲线确定,则渐近线确定吗?反过来呢?
提示:当双曲线的方程确定后,其渐近线方程也就确定了;反过来,确定的渐近线却对应着无数条双曲线,如具有相同的渐近线y=±x的双曲线可设为-=λ(λ≠0,λ∈R),当λ>0时,焦点在x轴上,当λ<0时,焦点在y轴上.
3.判断正误.(正确的画“√”,错误的画“×”)
(1)共渐近线的双曲线的离心率相同.( × )
(2)双曲线-=1与-=1(a>0,b>0)的渐近线相同.(× )
(3)双曲线-=1的渐近线方程是3x±2y=0.( √ )
典例分析
例1. (链接教科书第124页练习1题)求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
[解] 双曲线的方程化为标准形式是-=1,
∴a2=9,b2=4,∴a=3,b=2,c=.
又双曲线的焦点在x轴上,∴顶点坐标为(-3,0),(3,0),
焦点坐标为(-,0),(,0),
实轴长2a=6,虚轴长2b=4,
离心率e==,渐近线方程为y=±x.
小结1.由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准形式是解决此类题的关键;
(2)由标准方程确定焦点位置,确定a,b的值;
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
[注意] 求性质时一定要注意焦点的位置.
例2. (链接教科书第124页练习2题)(1)以椭圆+=1的顶点为顶点,离心率为2的双曲线方程为( )
A.-=1 B.-=1 C.-=1或-=1 D.以上都不对
(2)过点(2,-2)且与-y2=1有相同渐近线的双曲线的标准方程为___-=1._____.
小结2.求双曲线的标准方程的方法与技巧
(1)一般情况下,求双曲线的标准方程关键是确定a,b的值和焦点所在的坐标轴,若给出双曲线的顶点坐标或焦点坐标,则焦点所在的坐标轴易得.再结合c2=a2+b2及e=列关于a,b的方程(组),解方程(组)可得标准方程;
(2)如果已知双曲线的渐近线方程为y=±x,那么此双曲线方程可设为-=λ(λ≠0).
例3. 如图所示,F1和F2分别是双曲线-=1(a>0,b>0)的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为__1+______.
小结3.求双曲线离心率的两种方法
(1)直接法:若已知a,c可直接利用e=求解,若已知a,b,可利用e= 求解;
(2)方程法:若无法求出a,b,c的具体值,但根据条件可确定a,b,c之间的关系,可通过b2=c2-a2,将关系式转化为关于a,c的齐次方程,借助于e=,转化为关于e的n次方程求解.
1.已知双曲线的实轴和虚轴等长,且过点(5,3),则双曲线方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析:选D 由题意知,所求双曲线是等轴双曲线,设其方程为x2-y2=λ(λ≠0),将点(5,3)代入方程,可得λ=52-32=16,所以双曲线方程为x2-y2=16,即-=1.
2.(2020·全国卷Ⅲ)设双曲线C:-=1(a>0,b>0)的一条渐近线为y=x,则C的离心率为________.
解析:由双曲线的一条渐近线为y=x可知,=,即b=a.在双曲线中,c2=a2+b2,所以c2=3a2,所以e==.
答案:
