人教版数学八年级下册17.2勾股定理的逆定理课件(15张ppt)
文档属性
| 名称 | 人教版数学八年级下册17.2勾股定理的逆定理课件(15张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 339.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 13:06:27 | ||
图片预览




文档简介
(共16张PPT)
勾股定理的逆定理
逆定理:
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
勾股定理:
直角三角形的两直角边为a ,b , 斜边为 c ,则有
a2+ b2=c2
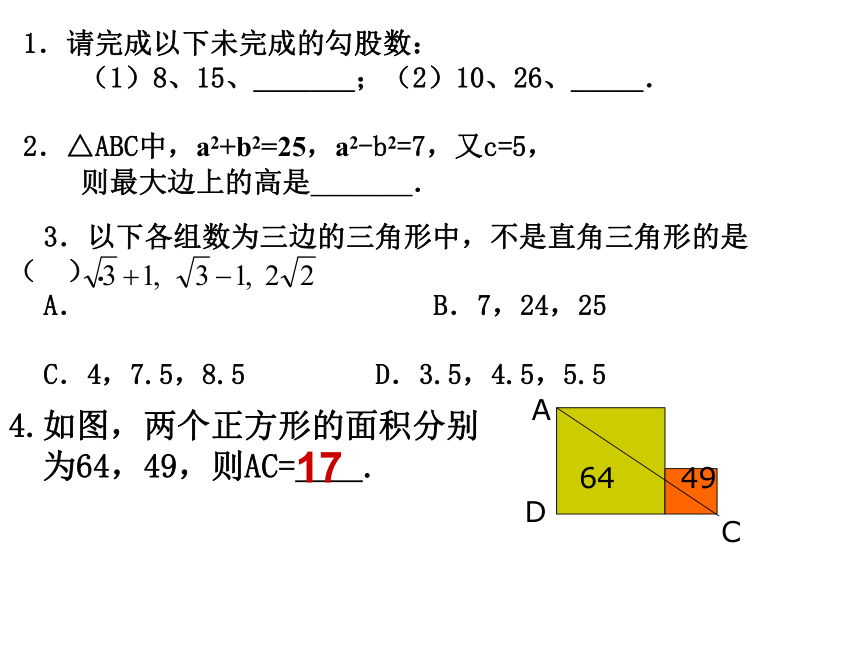
3.以下各组数为三边的三角形中,不是直角三角形的是( ).
A. B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
1.请完成以下未完成的勾股数:
(1)8、15、_______;(2)10、26、_____.
2.△ABC中,a2+b2=25,a2-b2=7,又c=5,
则最大边上的高是_______.
4.如图,两个正方形的面积分别
为64,49,则AC= .
A
D
C
64
49
17
5、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
6.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;
7.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,
此三角形为_____三角形.
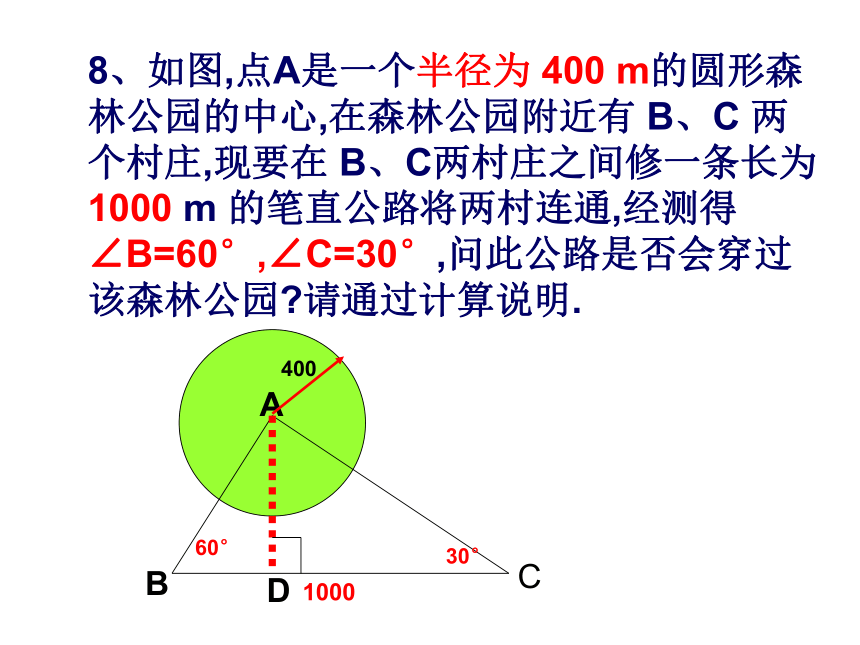
8、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园 请通过计算说明.
A
B
C
400
1000
60°
30°
D
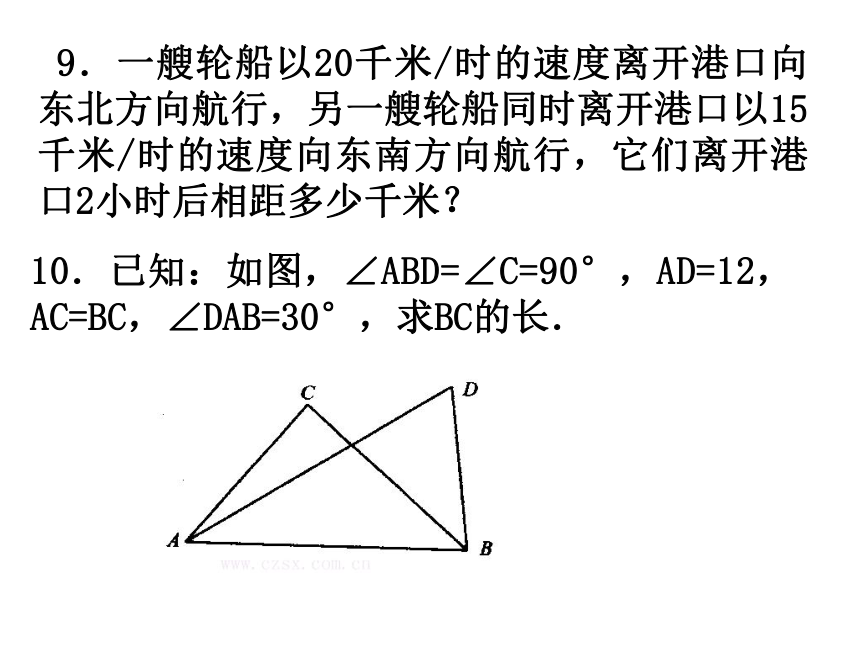
9.一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?
10.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
11、如图,已知:CD⊥AB于D,
且有
求证:△ACB为直角三角形
A
B
D
C
CD=
cm, AD=2cm, AC⊥AB。
12、已知:在四边形ABCD中,AB=3cm, BC=5cm,
求:S四边形ABCD
∵AC⊥AB(已知)
∴ AC2+AB2=BC2(勾股定理)
∵ AB=3cm,BC=5cm
又∵CD=2 cm AD=2cm(已知)
∴ AC2=16 , CD2+AD2=12+4=16
∴ AC2=CD2+AD2
∴ ∠ADC=900(勾股定理的逆定理
∴ S四边形ABCD=S △ ABC+ S△ ACD
∴
= ×3 × 4+ × 2 2
=6+2 (cm2)
= AB AC+ AD CD
解(1)
13、如图:边长为4的正方形ABCD中,F是DC的中点,
且CE= BC,则AF⊥EF,试说明理由
解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC
∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25
∴AD=4,DF=2,FC=2,EC=1
∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF
A
边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标,(3)AB1所在的直线解析式。
O
C
B
A
B1
D
1
2
3
E
1、如图,在四边形ABCD中,∠BAD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
2、已知,如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点,
求证:BD2+CD2=2AD2.
A
B
C
A
C
P
A
C
探索与提高2:
如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:
勾股定理的逆定理
逆定理:
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
勾股定理:
直角三角形的两直角边为a ,b , 斜边为 c ,则有
a2+ b2=c2
3.以下各组数为三边的三角形中,不是直角三角形的是( ).
A. B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
1.请完成以下未完成的勾股数:
(1)8、15、_______;(2)10、26、_____.
2.△ABC中,a2+b2=25,a2-b2=7,又c=5,
则最大边上的高是_______.
4.如图,两个正方形的面积分别
为64,49,则AC= .
A
D
C
64
49
17
5、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
6.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;
7.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,
此三角形为_____三角形.
8、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园 请通过计算说明.
A
B
C
400
1000
60°
30°
D
9.一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?
10.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
11、如图,已知:CD⊥AB于D,
且有
求证:△ACB为直角三角形
A
B
D
C
CD=
cm, AD=2cm, AC⊥AB。
12、已知:在四边形ABCD中,AB=3cm, BC=5cm,
求:S四边形ABCD
∵AC⊥AB(已知)
∴ AC2+AB2=BC2(勾股定理)
∵ AB=3cm,BC=5cm
又∵CD=2 cm AD=2cm(已知)
∴ AC2=16 , CD2+AD2=12+4=16
∴ AC2=CD2+AD2
∴ ∠ADC=900(勾股定理的逆定理
∴ S四边形ABCD=S △ ABC+ S△ ACD
∴
= ×3 × 4+ × 2 2
=6+2 (cm2)
= AB AC+ AD CD
解(1)
13、如图:边长为4的正方形ABCD中,F是DC的中点,
且CE= BC,则AF⊥EF,试说明理由
解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC
∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25
∴AD=4,DF=2,FC=2,EC=1
∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF
A
边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标,(3)AB1所在的直线解析式。
O
C
B
A
B1
D
1
2
3
E
1、如图,在四边形ABCD中,∠BAD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
2、已知,如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点,
求证:BD2+CD2=2AD2.
A
B
C
A
C
P
A
C
探索与提高2:
如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:
