人教版数学八年级下册 18.1.2 平行四边形的判定 课件(29张ppt)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 平行四边形的判定 课件(29张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 402.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 12:08:43 | ||
图片预览





文档简介
(共29张PPT)
复习回顾
有两组对边分别平行的四边形叫做平行四边形.
平行四边形的对边相等;
平行四边形的对角相等.
平行四边形的对角线互相平分。
性质:
定义:
通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
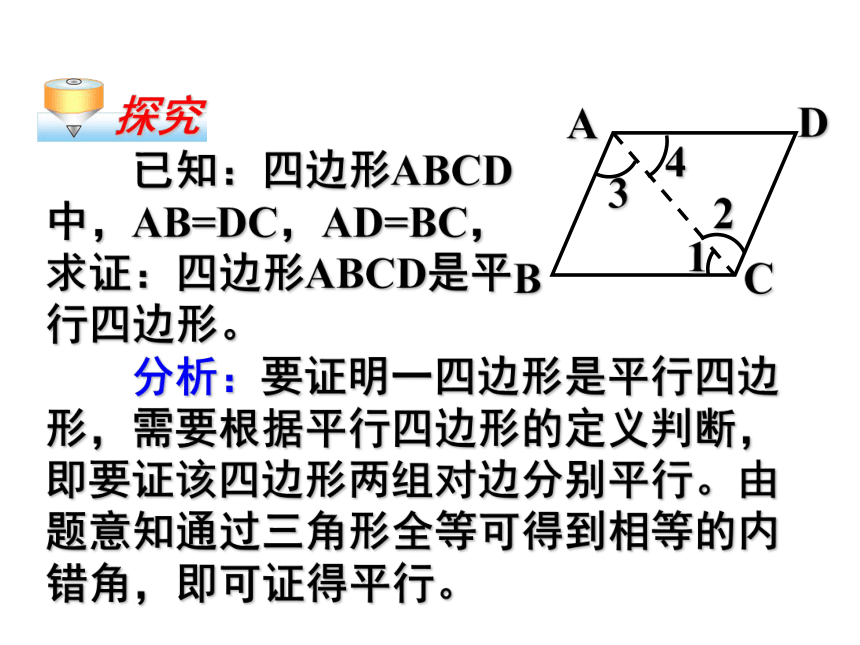
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形。
A
B
C
D
1
2
3
4
分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。由题意知通过三角形全等可得到相等的内错角,即可证得平行。
探究
A
B
C
D
1
2
3
4
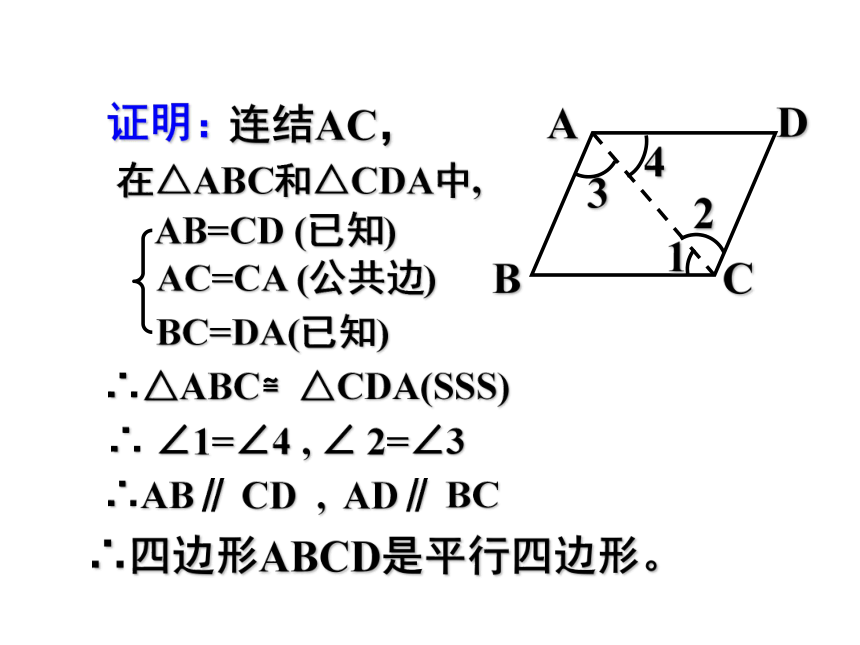
证明:
连结AC,
在△ABC和△CDA中,
AB=CD (已知)
BC=DA(已知)
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
由上述证明可以得到平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形。
当一个四边形对角分别相等,这个四边形是平行四边形吗?
当一个四边形对角线互相平分,这个四边形是平行四边形吗?
类似地,思考下列问题:
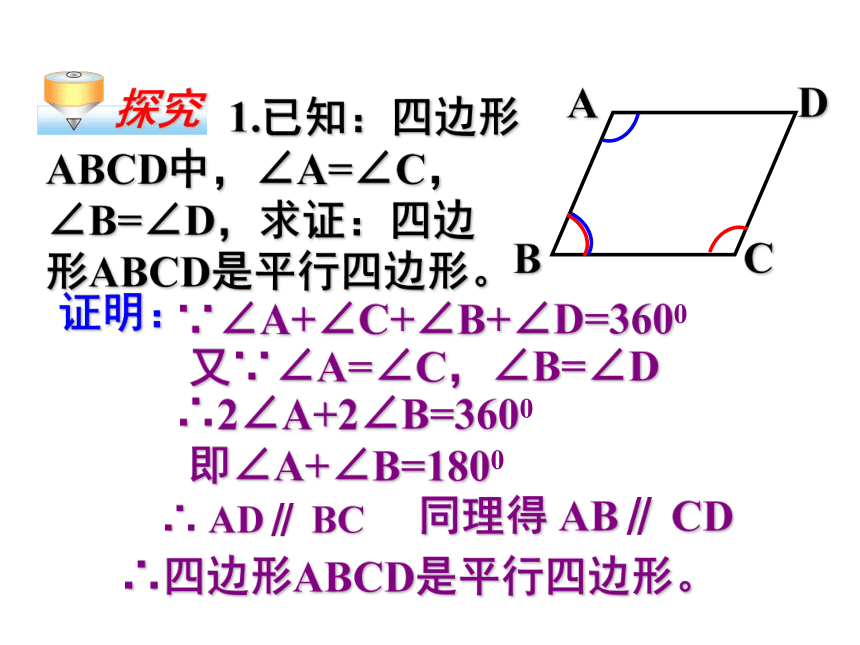
1.已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边 形ABCD是平行四边形。
A
B
C
D
证明:
又∵∠A=∠C,∠B=∠D
∵∠A+∠C+∠B+∠D=3600
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴ AD∥ BC
∴四边形ABCD是平行四边形。
同理得 AB∥ CD
探究
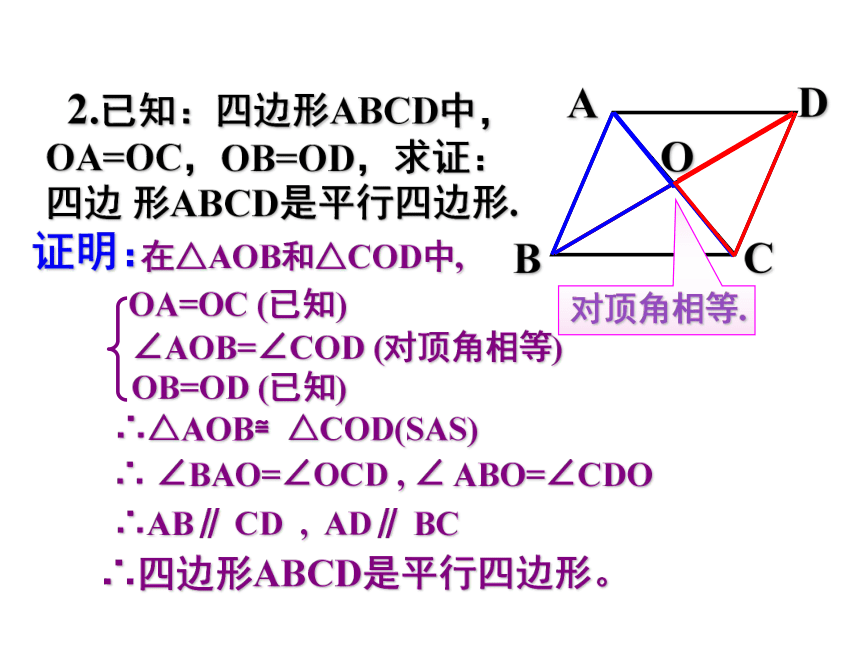
2.已知:四边形ABCD中,OA=OC,OB=OD,求证:四边 形ABCD是平行四边形.
证明:
A
B
C
D
O
对顶角相等.
在△AOB和△COD中,
OA=OC (已知)
OB=OD (已知)
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
梳理
平行四边形的判定定理:
判定 1 定义:两组对边分别平行的四边形是平行四边形。
判定3 两组对角分别相等的四边形是平行四边形。
判定4 两条对角线互相平分的四边形是平行四边形。
判定2 两组对边分别相等的四边形是平行四边形。
A
B
C
D
O
AB=DC AD=BC
ABCD
AB∥DC AD∥BC
ABCD
∠ABC=∠ADC ∠BAD=∠BCD
ABCD
OA=OC OB=OD
ABCD
几何语言描述判定:
1、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4
C.2:3:2:3
B.2:2:3:3
D.2:3:3:2
需要两组对角分别相等.
C
2、在下列条件中,能判定四边形ABCD为平行四边形的是( )
A.AB=AD,CB=CD
B.AB∥CD,AD=BC
D.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC
A
B
C
D
C
若一组对边平行且相等,这个四边形是平行四边形吗?
已知:四边形ABCD中,AD=BC,AD∥BC,求证:四边 形ABCD是平行四边形。
A
B
C
D
1
2
在△ABC和△CDA中,
AD=BC (已知)
AC=CA (公共边)
∠1=∠2 (已证)
∴△ABC≌△CDA(SAS)
∴ AB=CD
∴四边形ABCD是平行四边形。
证明:
∵AB∥ CD
∴ ∠1=∠2
又∵AD=BC
探究
还可以怎样证明?
由上题我们得到平行四边形的又一个判定定理:
一组对边平行且相等的四边形是平行四边形。
A
B
C
D
ABCD
“ ”读作“平行且相等”.
AD BC
归纳
填空题: 如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
8
4
两组对边分别相等的四边形是平行四边形
A
B
C
D
练习
②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
120
60
60
两组对角分别相等的四边形是平行四边形
A
B
C
D
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
6
一组对边平行且相等的四边形是平行四边形
A
B
C
D
④如果AC、BD相交于点O,AC=8cm,BD=10cm,且AO=____cm,DO=____cm,那么四边形ABCD是平行四边形。
4
5
对角线互相平分的四边形是平行四边形
A
B
C
D
O
例1 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形.
D
A
B
C
E
F
证明: ABCD中
AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 ∵BO=DO
O
∴ 四边形BFDE是平行四边形.
例题讲解
例2 如图,D、E分别是△ABC的边AB、AC的中点,
分析:要证明线段的倍分关系,可将DE加倍后证明与BC相等。从而转化为证明平行四边形的对边的关系, 于是可作辅助线,利用全等三角形来证明相应的边相等.
求证:DE∥BC,
D
E
B
C
A
证明:延长DE至F,使EF=DE,连接FC、DC、AF.
∵ AE=CE,
D
E
B
C
A
F
∴四边形DBCF是平行四边形.
∴DE∥BC,
∴四边形ADCF是平行四边形,
D
E
B
C
A
有什么发现呢?
我们把连接三角形两边中点的线段叫做三角形的中位线。
由上题可得三角形中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
A
B
C
D
E
如上图,在△ABC中 AD=BD,AE=CE
DE∥BC
归纳
A
B
C
D
E
F
一个三角形有几条中位线?中位线和三角形的中线一样吗?
要把三角形的中位线与三角形的中线区分开:三角形中线是连结一顶点和它的对边中点的线段,而三角形中位线是连结三角形两边中点的线段.
一个三角形有三条中位线。
A
B
C
H
D
E
F
G
1、如图,在四边形ABCD中, E,F,G,H分别为各边的中点。求证:四边形EFGH是平行四边形。
练习
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴四边形EFGH是平行四边形.
∴EF∥AC,
HG∥AC,
A
B
C
H
D
E
F
G
∴EF GH
2、四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形。
A
B
C
D
E
F
你会证了吗?试试吧!
平行四边形的判定:
判定 1 定义:两组对边分别平行的四边形是平行四边形。
判定3 两组对角分别相等的四边形是平行四边形。
判定4 两条对角线互相平分的四边形是平行四边形。
判定2 两组对边分别相等的四边形是平行四边形。
判定5 一组对边平行且相等的四边形是平行四边形。
定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
在△ABC中 AD=BD,AE=CE
DE∥BC
三角形的中位线:
定理:
复习回顾
有两组对边分别平行的四边形叫做平行四边形.
平行四边形的对边相等;
平行四边形的对角相等.
平行四边形的对角线互相平分。
性质:
定义:
通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形。
A
B
C
D
1
2
3
4
分析:要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。由题意知通过三角形全等可得到相等的内错角,即可证得平行。
探究
A
B
C
D
1
2
3
4
证明:
连结AC,
在△ABC和△CDA中,
AB=CD (已知)
BC=DA(已知)
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
由上述证明可以得到平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形。
当一个四边形对角分别相等,这个四边形是平行四边形吗?
当一个四边形对角线互相平分,这个四边形是平行四边形吗?
类似地,思考下列问题:
1.已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边 形ABCD是平行四边形。
A
B
C
D
证明:
又∵∠A=∠C,∠B=∠D
∵∠A+∠C+∠B+∠D=3600
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴ AD∥ BC
∴四边形ABCD是平行四边形。
同理得 AB∥ CD
探究
2.已知:四边形ABCD中,OA=OC,OB=OD,求证:四边 形ABCD是平行四边形.
证明:
A
B
C
D
O
对顶角相等.
在△AOB和△COD中,
OA=OC (已知)
OB=OD (已知)
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
梳理
平行四边形的判定定理:
判定 1 定义:两组对边分别平行的四边形是平行四边形。
判定3 两组对角分别相等的四边形是平行四边形。
判定4 两条对角线互相平分的四边形是平行四边形。
判定2 两组对边分别相等的四边形是平行四边形。
A
B
C
D
O
AB=DC AD=BC
ABCD
AB∥DC AD∥BC
ABCD
∠ABC=∠ADC ∠BAD=∠BCD
ABCD
OA=OC OB=OD
ABCD
几何语言描述判定:
1、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4
C.2:3:2:3
B.2:2:3:3
D.2:3:3:2
需要两组对角分别相等.
C
2、在下列条件中,能判定四边形ABCD为平行四边形的是( )
A.AB=AD,CB=CD
B.AB∥CD,AD=BC
D.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC
A
B
C
D
C
若一组对边平行且相等,这个四边形是平行四边形吗?
已知:四边形ABCD中,AD=BC,AD∥BC,求证:四边 形ABCD是平行四边形。
A
B
C
D
1
2
在△ABC和△CDA中,
AD=BC (已知)
AC=CA (公共边)
∠1=∠2 (已证)
∴△ABC≌△CDA(SAS)
∴ AB=CD
∴四边形ABCD是平行四边形。
证明:
∵AB∥ CD
∴ ∠1=∠2
又∵AD=BC
探究
还可以怎样证明?
由上题我们得到平行四边形的又一个判定定理:
一组对边平行且相等的四边形是平行四边形。
A
B
C
D
ABCD
“ ”读作“平行且相等”.
AD BC
归纳
填空题: 如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
8
4
两组对边分别相等的四边形是平行四边形
A
B
C
D
练习
②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
120
60
60
两组对角分别相等的四边形是平行四边形
A
B
C
D
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
6
一组对边平行且相等的四边形是平行四边形
A
B
C
D
④如果AC、BD相交于点O,AC=8cm,BD=10cm,且AO=____cm,DO=____cm,那么四边形ABCD是平行四边形。
4
5
对角线互相平分的四边形是平行四边形
A
B
C
D
O
例1 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形.
D
A
B
C
E
F
证明: ABCD中
AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 ∵BO=DO
O
∴ 四边形BFDE是平行四边形.
例题讲解
例2 如图,D、E分别是△ABC的边AB、AC的中点,
分析:要证明线段的倍分关系,可将DE加倍后证明与BC相等。从而转化为证明平行四边形的对边的关系, 于是可作辅助线,利用全等三角形来证明相应的边相等.
求证:DE∥BC,
D
E
B
C
A
证明:延长DE至F,使EF=DE,连接FC、DC、AF.
∵ AE=CE,
D
E
B
C
A
F
∴四边形DBCF是平行四边形.
∴DE∥BC,
∴四边形ADCF是平行四边形,
D
E
B
C
A
有什么发现呢?
我们把连接三角形两边中点的线段叫做三角形的中位线。
由上题可得三角形中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
A
B
C
D
E
如上图,在△ABC中 AD=BD,AE=CE
DE∥BC
归纳
A
B
C
D
E
F
一个三角形有几条中位线?中位线和三角形的中线一样吗?
要把三角形的中位线与三角形的中线区分开:三角形中线是连结一顶点和它的对边中点的线段,而三角形中位线是连结三角形两边中点的线段.
一个三角形有三条中位线。
A
B
C
H
D
E
F
G
1、如图,在四边形ABCD中, E,F,G,H分别为各边的中点。求证:四边形EFGH是平行四边形。
练习
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴四边形EFGH是平行四边形.
∴EF∥AC,
HG∥AC,
A
B
C
H
D
E
F
G
∴EF GH
2、四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形。
A
B
C
D
E
F
你会证了吗?试试吧!
平行四边形的判定:
判定 1 定义:两组对边分别平行的四边形是平行四边形。
判定3 两组对角分别相等的四边形是平行四边形。
判定4 两条对角线互相平分的四边形是平行四边形。
判定2 两组对边分别相等的四边形是平行四边形。
判定5 一组对边平行且相等的四边形是平行四边形。
定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
在△ABC中 AD=BD,AE=CE
DE∥BC
三角形的中位线:
定理:
