1.1 空间几何体的结构(Word含答案)
文档属性
| 名称 | 1.1 空间几何体的结构(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 20:10:42 | ||
图片预览

文档简介
1.1 空间几何体的结构
一、选择题(共10小题;共50分)
1. 如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是 .
A. 棱柱 B. 棱台
C. 棱柱与棱锥的组合体 D. 不能确定
2. 如果圆台两底面的半径分别是 和 ,则与两底面平行且等距离的截面面积是
A. B. C. D.
3. 用半径为 ,圆心角为 的扇形围成圆锥的侧面,则该圆锥的高是
A. B. C. D.
4. 用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是 ,这个截面把圆锥的母线分成的两段的比是
A. B. C. D.
5. 用长为 ,宽为 的矩形做侧面围成一个圆柱,则圆柱的轴截面的面积为
A. B. C. D.
6. 图中是四棱台的侧面展开图的是
A. B.
C. D.
7. 右图是由下面哪个平面图旋转后得到的
A. B.
C. D.
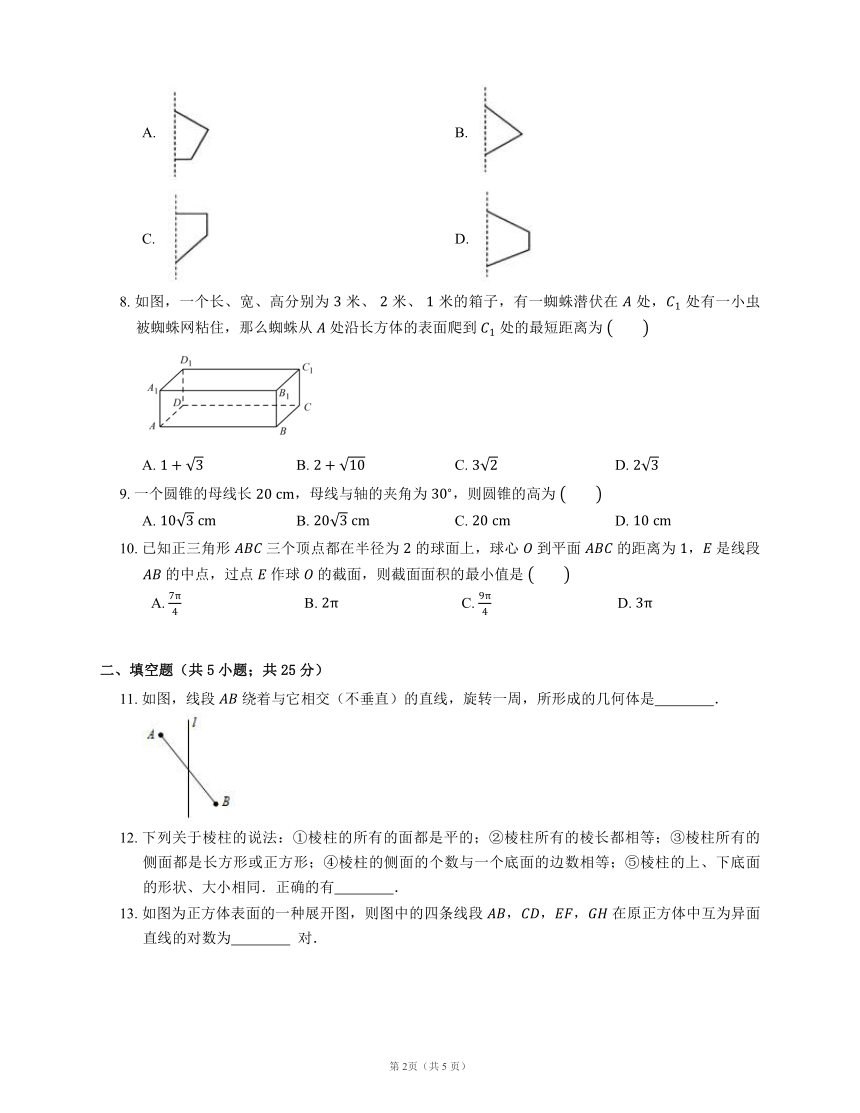
8. 如图,一个长、宽、高分别为 米、 米、 米的箱子,有一蜘蛛潜伏在 处, 处有一小虫被蜘蛛网粘住,那么蜘蛛从 处沿长方体的表面爬到 处的最短距离为
A. B. C. D.
9. 一个圆锥的母线长 ,母线与轴的夹角为 ,则圆锥的高为
A. B. C. D.
10. 已知正三角形 三个顶点都在半径为 的球面上,球心 到平面 的距离为 , 是线段 的中点,过点 作球 的截面,则截面面积的最小值是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如图,线段 绕着与它相交(不垂直)的直线,旋转一周,所形成的几何体是 .
12. 下列关于棱柱的说法:①棱柱的所有的面都是平的;②棱柱所有的棱长都相等;③棱柱所有的侧面都是长方形或正方形;④棱柱的侧面的个数与一个底面的边数相等;⑤棱柱的上、下底面的形状、大小相同.正确的有 .
13. 如图为正方体表面的一种展开图,则图中的四条线段 ,,, 在原正方体中互为异面直线的对数为 对.
14. 一个圆柱的母线长为 ,底面半径为 ,则圆柱的一个轴截面的面积是 .
15. 如图,在棱长为 的正方体 中,,截面 ,截面 ,则截面 和截面 面积之和为 .
三、解答题(共3小题;共39分)
16. 把四个半径都是 的球中的三个放在桌面上,使它们两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离.
17. 设点 是球 的半径 的中点,分别过点 , 作垂直于 的平面,截球面得两个圆,求这两个圆的面积的比值.
18. 经过球面上不同两点的大圆有多少个 并说明理由.
答案
第一部分
1. A
2. B 【解析】截面圆的半径为 ,面积为 .
3. B
4. B 【解析】利用面积比等于相似比的平方求解.
5. B
【解析】若 为底面周长,则圆柱的高为 ,此时圆柱的底面直径为 ,其轴截面的面积为 ;若 为底面周长,则圆柱的高为 ,此时圆柱的底面直径为 ,其轴截面的面积为 .
6. D 【解析】四棱台的侧面是梯形,则侧面展开图不是 A、B、C 的形状,
7. A
8. C
9. A
10. C
第二部分
11. 两个有公共顶点且底面互相平行的圆锥的侧面
12. ①④⑤
13.
【解析】平面图形的翻折应注意翻折前后相对位置的变化,则 ,, 和 在原正方体中,显然 与 , 与 , 与 都是异面直线,而 与 相交, 与 相交, 与 平行.
故互为异面的直线有且只有 对.
14.
【解析】由题意知圆柱的轴截面是以下底面圆的直径为长,以圆柱的母线为宽的矩形,所以轴面的面积 .
15.
【解析】因为在棱长为 的正方体 中,,截面 ,截面 ,
所以 ,,
所以
因为 ,,
所以
解得
所以截面 和截面 面积之和:
第三部分
16. 由题意,四球心组成棱长为 的正四面体的四个顶点,
则正四面体的高 .
而第四个球的最高点到第四个球的球心距离为球的半径 ,且三个球心到桌面的距离都为 ,
故第四个球的最高点与桌面的距离为 .
17. .
18. 一个或无数个,理由略.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是 .
A. 棱柱 B. 棱台
C. 棱柱与棱锥的组合体 D. 不能确定
2. 如果圆台两底面的半径分别是 和 ,则与两底面平行且等距离的截面面积是
A. B. C. D.
3. 用半径为 ,圆心角为 的扇形围成圆锥的侧面,则该圆锥的高是
A. B. C. D.
4. 用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是 ,这个截面把圆锥的母线分成的两段的比是
A. B. C. D.
5. 用长为 ,宽为 的矩形做侧面围成一个圆柱,则圆柱的轴截面的面积为
A. B. C. D.
6. 图中是四棱台的侧面展开图的是
A. B.
C. D.
7. 右图是由下面哪个平面图旋转后得到的
A. B.
C. D.
8. 如图,一个长、宽、高分别为 米、 米、 米的箱子,有一蜘蛛潜伏在 处, 处有一小虫被蜘蛛网粘住,那么蜘蛛从 处沿长方体的表面爬到 处的最短距离为
A. B. C. D.
9. 一个圆锥的母线长 ,母线与轴的夹角为 ,则圆锥的高为
A. B. C. D.
10. 已知正三角形 三个顶点都在半径为 的球面上,球心 到平面 的距离为 , 是线段 的中点,过点 作球 的截面,则截面面积的最小值是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如图,线段 绕着与它相交(不垂直)的直线,旋转一周,所形成的几何体是 .
12. 下列关于棱柱的说法:①棱柱的所有的面都是平的;②棱柱所有的棱长都相等;③棱柱所有的侧面都是长方形或正方形;④棱柱的侧面的个数与一个底面的边数相等;⑤棱柱的上、下底面的形状、大小相同.正确的有 .
13. 如图为正方体表面的一种展开图,则图中的四条线段 ,,, 在原正方体中互为异面直线的对数为 对.
14. 一个圆柱的母线长为 ,底面半径为 ,则圆柱的一个轴截面的面积是 .
15. 如图,在棱长为 的正方体 中,,截面 ,截面 ,则截面 和截面 面积之和为 .
三、解答题(共3小题;共39分)
16. 把四个半径都是 的球中的三个放在桌面上,使它们两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离.
17. 设点 是球 的半径 的中点,分别过点 , 作垂直于 的平面,截球面得两个圆,求这两个圆的面积的比值.
18. 经过球面上不同两点的大圆有多少个 并说明理由.
答案
第一部分
1. A
2. B 【解析】截面圆的半径为 ,面积为 .
3. B
4. B 【解析】利用面积比等于相似比的平方求解.
5. B
【解析】若 为底面周长,则圆柱的高为 ,此时圆柱的底面直径为 ,其轴截面的面积为 ;若 为底面周长,则圆柱的高为 ,此时圆柱的底面直径为 ,其轴截面的面积为 .
6. D 【解析】四棱台的侧面是梯形,则侧面展开图不是 A、B、C 的形状,
7. A
8. C
9. A
10. C
第二部分
11. 两个有公共顶点且底面互相平行的圆锥的侧面
12. ①④⑤
13.
【解析】平面图形的翻折应注意翻折前后相对位置的变化,则 ,, 和 在原正方体中,显然 与 , 与 , 与 都是异面直线,而 与 相交, 与 相交, 与 平行.
故互为异面的直线有且只有 对.
14.
【解析】由题意知圆柱的轴截面是以下底面圆的直径为长,以圆柱的母线为宽的矩形,所以轴面的面积 .
15.
【解析】因为在棱长为 的正方体 中,,截面 ,截面 ,
所以 ,,
所以
因为 ,,
所以
解得
所以截面 和截面 面积之和:
第三部分
16. 由题意,四球心组成棱长为 的正四面体的四个顶点,
则正四面体的高 .
而第四个球的最高点到第四个球的球心距离为球的半径 ,且三个球心到桌面的距离都为 ,
故第四个球的最高点与桌面的距离为 .
17. .
18. 一个或无数个,理由略.
第1页(共1 页)
