1.2 空间几何体的三视图和直观图(Word含答案)
文档属性
| 名称 | 1.2 空间几何体的三视图和直观图(Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 20:11:47 | ||
图片预览

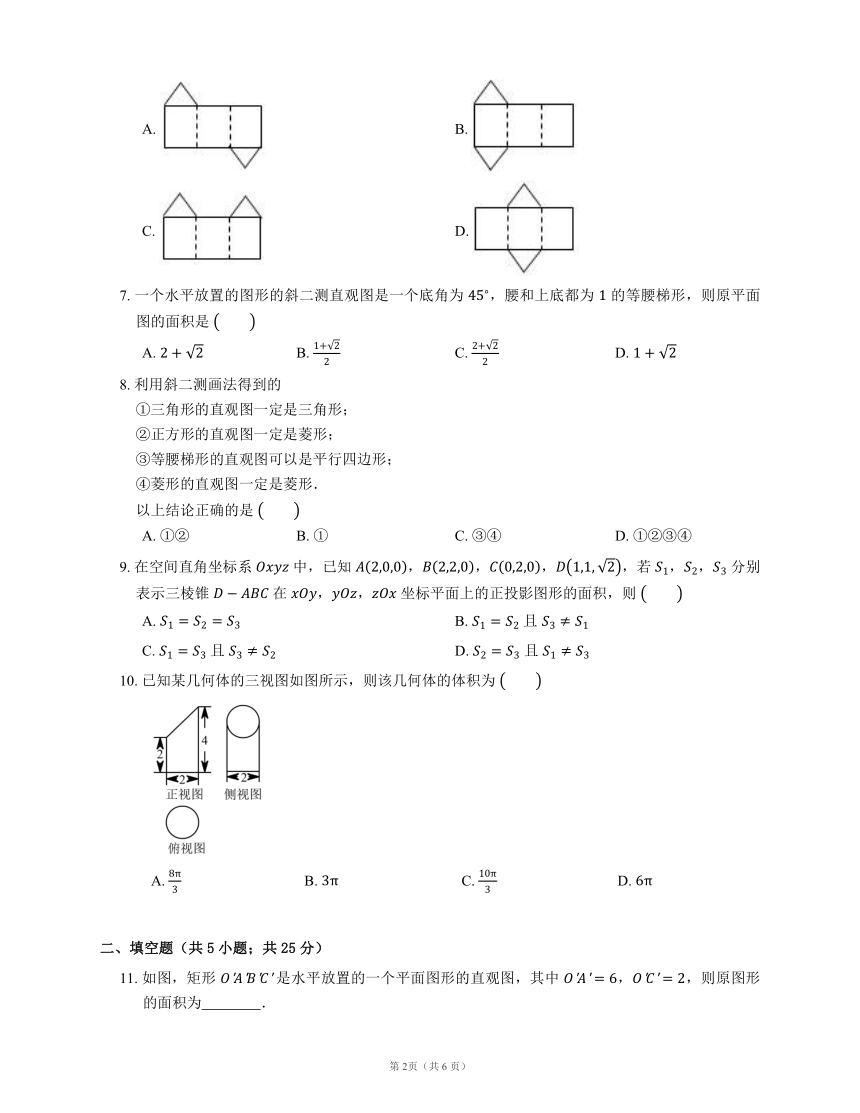

文档简介
1.2 空间几何体的三视图和直观图
一、选择题(共10小题;共50分)
1. 梯形的直观图是
A. 三角形 B. 梯形 C. 平行四边形 D. 五边形
2. 如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是
A. 三棱锥 B. 三棱柱 C. 四棱锥 D. 四棱柱
3. 如果一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底均为 的等腰梯形,那么原平面图形的面积是
A. B. C. D.
4. 如图所示,一个空间几何体的主视图和左视图都是边长为 的正方形,俯视图是一个直径为 的圆,那么这个几何体的全面积为
A. B. C. D.
5. 利用斜二测画法可以得到:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形,以上结论正确的是
A. ①② B. ① C. ③④ D. ①②③④
6. 下列图形中, 不是三棱柱的展开图.
A. B.
C. D.
7. 一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底都为 的等腰梯形,则原平面图的面积是
A. B. C. D.
8. 利用斜二测画法得到的
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是
A. ①② B. ① C. ③④ D. ①②③④
9. 在空间直角坐标系 中,已知 ,,,,若 ,, 分别表示三棱锥 在 ,, 坐标平面上的正投影图形的面积,则
A. B.
C. D.
10. 已知某几何体的三视图如图所示,则该几何体的体积为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如图,矩形 是水平放置的一个平面图形的直观图,其中 ,,则原图形的面积为 .
12. 如图所示是水平放置的 ( 为 边上的中线)的直观图,试按此图判定原 中的四条线段 中最长的线段是 ,最短的线段是 .
13. 等腰梯形 ,上底 ,腰 ,下底 ,以下底所在直线为 轴,则由斜二测画法画出的直观图 的面积为 .
14. 已知 在一投射面内的平行投影是 ,则 的重心 在投射面内的平行投影 应为 的 .
15. 利用斜二测画法画直观图时,
①三角形的直观图还是三角形;
②平行四边形的直观图还是平行四边形;
③正方形的直观图还是正方形;
④菱形的直观图还是菱形.
其中正确的说法是 .
三、解答题(共3小题;共39分)
16. 用斜二测画法作出宽为 ,长为 的矩形的直观图.
17. 如图是截去一角的长方体,画出它的三视图.
18. 一个四边形的直观图是一个底角为 ,腰和上底长均为 的等腰梯形,求原四边形的面积.
答案
第一部分
1. B
2. B
3. A 【解析】提示:直观图和原图如图所示.
根据题意及等腰梯形的性质可求得 ,所以原图中 .
4. A
5. A
6. C
7. A
8. B
9. D 【解析】 在平面上的投影为 ,故 .
设 在 和 平面上的投影分别为 和 ,
则 在 和 平面上的投影分别为 和 .
∵ ,故 .
10. B
【解析】两个这样的几何体可以拼成一个底面半径为 、高为 的圆柱,所以 .
第二部分
11.
12. ,,
【解析】原图如下:
因为 ,而 ,所以 .
13.
【解析】
因为 ,
所以 .
所以 .
所以直观图 的面积为 .
14. 重心
15. ①②
第三部分
16. 采用斜二测画法,即在已知图形所在的空间中取水平平面,作 轴, 轴,使 ,然后依据平行投影的有关性质逐一作图(如图).
(i)在矩形 中取 , 所在边分别为 轴与 轴,相交于点 ( 与 重合),画对应的 轴, 轴,使 .
(ii)在 轴上取 ,,使 ,在 轴上取 ,使 ,过 作 平行 轴的直线,且等于 长.
(iii)连接 ,所得四边形 就是矩形 的直观图.
17. 如图所示.
18. 图①是四边形的直观图,
取 所在直线为 轴,因为 ,
所以取 所在直线为 轴,
过点 作 交 于点 ,
则 ,.
又因为梯形 为等腰梯形,且底角为 ,
所以 为等腰直角三角形,
所以 ,
所以 .
再建立一个直角坐标系 ,如图②,
在 轴上截取线段 ,在 轴上截取线段 ,
过 作 ,截取 ,连接 ,
则四边形 就是四边形 的实际图形,四边形 为直角梯形,上底 ,下底 ,高 ,
所以 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 梯形的直观图是
A. 三角形 B. 梯形 C. 平行四边形 D. 五边形
2. 如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是
A. 三棱锥 B. 三棱柱 C. 四棱锥 D. 四棱柱
3. 如果一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底均为 的等腰梯形,那么原平面图形的面积是
A. B. C. D.
4. 如图所示,一个空间几何体的主视图和左视图都是边长为 的正方形,俯视图是一个直径为 的圆,那么这个几何体的全面积为
A. B. C. D.
5. 利用斜二测画法可以得到:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形,以上结论正确的是
A. ①② B. ① C. ③④ D. ①②③④
6. 下列图形中, 不是三棱柱的展开图.
A. B.
C. D.
7. 一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底都为 的等腰梯形,则原平面图的面积是
A. B. C. D.
8. 利用斜二测画法得到的
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是
A. ①② B. ① C. ③④ D. ①②③④
9. 在空间直角坐标系 中,已知 ,,,,若 ,, 分别表示三棱锥 在 ,, 坐标平面上的正投影图形的面积,则
A. B.
C. D.
10. 已知某几何体的三视图如图所示,则该几何体的体积为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如图,矩形 是水平放置的一个平面图形的直观图,其中 ,,则原图形的面积为 .
12. 如图所示是水平放置的 ( 为 边上的中线)的直观图,试按此图判定原 中的四条线段 中最长的线段是 ,最短的线段是 .
13. 等腰梯形 ,上底 ,腰 ,下底 ,以下底所在直线为 轴,则由斜二测画法画出的直观图 的面积为 .
14. 已知 在一投射面内的平行投影是 ,则 的重心 在投射面内的平行投影 应为 的 .
15. 利用斜二测画法画直观图时,
①三角形的直观图还是三角形;
②平行四边形的直观图还是平行四边形;
③正方形的直观图还是正方形;
④菱形的直观图还是菱形.
其中正确的说法是 .
三、解答题(共3小题;共39分)
16. 用斜二测画法作出宽为 ,长为 的矩形的直观图.
17. 如图是截去一角的长方体,画出它的三视图.
18. 一个四边形的直观图是一个底角为 ,腰和上底长均为 的等腰梯形,求原四边形的面积.
答案
第一部分
1. B
2. B
3. A 【解析】提示:直观图和原图如图所示.
根据题意及等腰梯形的性质可求得 ,所以原图中 .
4. A
5. A
6. C
7. A
8. B
9. D 【解析】 在平面上的投影为 ,故 .
设 在 和 平面上的投影分别为 和 ,
则 在 和 平面上的投影分别为 和 .
∵ ,故 .
10. B
【解析】两个这样的几何体可以拼成一个底面半径为 、高为 的圆柱,所以 .
第二部分
11.
12. ,,
【解析】原图如下:
因为 ,而 ,所以 .
13.
【解析】
因为 ,
所以 .
所以 .
所以直观图 的面积为 .
14. 重心
15. ①②
第三部分
16. 采用斜二测画法,即在已知图形所在的空间中取水平平面,作 轴, 轴,使 ,然后依据平行投影的有关性质逐一作图(如图).
(i)在矩形 中取 , 所在边分别为 轴与 轴,相交于点 ( 与 重合),画对应的 轴, 轴,使 .
(ii)在 轴上取 ,,使 ,在 轴上取 ,使 ,过 作 平行 轴的直线,且等于 长.
(iii)连接 ,所得四边形 就是矩形 的直观图.
17. 如图所示.
18. 图①是四边形的直观图,
取 所在直线为 轴,因为 ,
所以取 所在直线为 轴,
过点 作 交 于点 ,
则 ,.
又因为梯形 为等腰梯形,且底角为 ,
所以 为等腰直角三角形,
所以 ,
所以 .
再建立一个直角坐标系 ,如图②,
在 轴上截取线段 ,在 轴上截取线段 ,
过 作 ,截取 ,连接 ,
则四边形 就是四边形 的实际图形,四边形 为直角梯形,上底 ,下底 ,高 ,
所以 .
第1页(共1 页)
