2.2 直线、平面平行的判定及其性质(Word含答案)
文档属性
| 名称 | 2.2 直线、平面平行的判定及其性质(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 662.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 11:42:58 | ||
图片预览


文档简介
2.2 直线、平面平行的判定及其性质
一、选择题(共10小题;共50分)
1. ,点 ,,点 ,,则能得到直线 直线 的是
A. B.
C. 且相交 D. ,,, 四点共面
2. 若平面 平面 ,则
A. 平面 内任一条直线与平面 平行
B. 平面 内任一条直线与平面 内任一条直线平行
C. 平面 内存在一条直线与平面 不平行
D. 平面 内一条直线与平面 内一条直线有可能相交
3. 已知 是 所在平面外一点,, 交线段 ,, 于点 ,,,若 ,则 等于
A. B. C. D.
4. 平面 ,, 分别在 、 内,线段 ,, 共点于 , 在 、 之间.若 ,,,,则 的面积为
A. B. C. D.
5. 为矩形 所在平面外一点,矩形对角线交点为 , 为 的中点,给出四个结论:① ;② ;③ ;④ ;⑤ ,其中正确的个数有
A. B. C. D.
6. 下列说法中,正确的是
A. 空间中没有交点的两条直线是平行直线
B. 一条直线和两条平行直线中的一条相交,则它和另一条直线也相交
C. 空间四条直线 ,,,,若 , 且 ,则
D. 分别在两个平面内的直线是平行直线
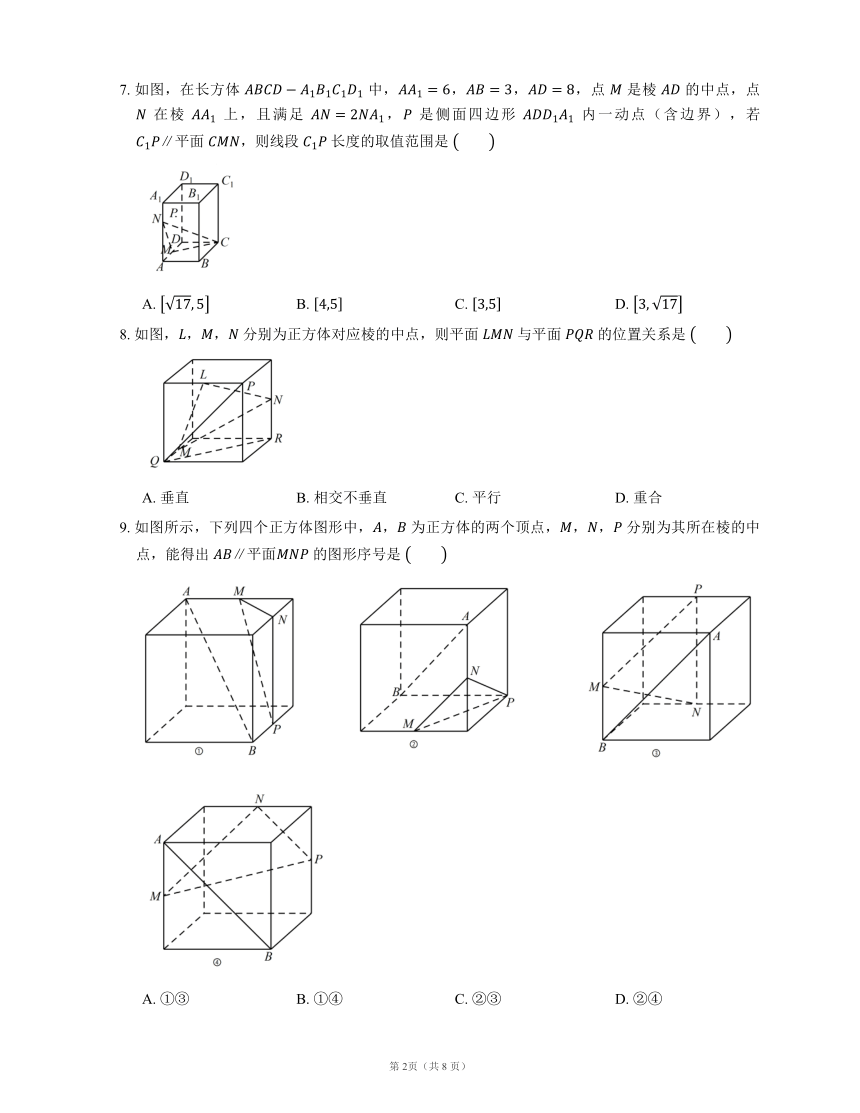
7. 如图,在长方体 中,,,,点 是棱 的中点,点 在棱 上,且满足 , 是侧面四边形 内一动点(含边界),若 ,则线段 长度的取值范围是
A. B. C. D.
8. 如图,,, 分别为正方体对应棱的中点,则平面 与平面 的位置关系是
A. 垂直 B. 相交不垂直 C. 平行 D. 重合
9. 如图所示,下列四个正方体图形中,, 为正方体的两个顶点,,, 分别为其所在棱的中点,能得出 的图形序号是
A. ①③ B. ①④ C. ②③ D. ②④
10. 如图所示,已知三棱锥 中,, 分别为 , 的中点,则下列结论正确的是
A. B.
C. D.
二、填空题(共5小题;共25分)
11. 直线 ,,平面 , 满足 ,,,则平面 , 的位置关系是 .
12. 在三棱锥 中, 是边长为 的正三角形,,平面 分别与 ,,, 交于点 ,,,., 分别是 , 的中点,如果 ,那么四边形 的面积为 .
13. 夹在两平行平面间的两条线段 , 相交于 (如图所示),已知 ,,.则线段 , 的长分别为 .
14. 如图所示,正方体 中,判断下列直线的位置关系:
(1)直线 与直线 的位置关系是 ;
(2)直线 与直线 的位置关系是 ;
(3)直线 与直线 的位置关系是 ;
(4)直线 与直线 的位置关系是 .
15. 考察下列三个命题:“”处都缺少同一个条件,补上这个条件使其构成真命题(其中 , 为直线,, 为平面),则此条件为 .
① ;② ;③ ;
三、解答题(共3小题;共39分)
16. 已知 和 分别是正方体 的棱 和棱 上的点,且 ,求证:四边形 是平行四边形.
17. 如图,四棱锥 中,,,,, 分别是线段 ,, 的中点, 与 交于 点, 是线段 上一点.求证:
(1);
(2).
18. 如图,正方形 中,, 分别为 , 的中点.在五棱锥 中, 为棱 的中点,平面 与棱 , 分别交于点 ,.求证:.
答案
第一部分
1. D 【解析】若 ,,, 四点共面,则直线 是平面 与平面 的交线,直线 是平面 与平面 的交线,由线面平行的性质得 .
2. A
3. B 【解析】由题意,,由相似三角形中面积比等于边长比的平方得 .
4. C 【解析】如图,因为 ,所以 ,,,
所以 ,
且由 知相似比为 ,
又由 ,,,
知 ,
所以 .
5. C
【解析】由题意知 ,则 ,且 .
6. C
7. A
8. C 【解析】如图,分别取另三条棱的中点 ,,,将平面 延展为平面正六边形 ,
因为 ,,且 与 相交, 与 相交,
所以 ,即 .
9. B 【解析】利用线面平行的定义判定.
10. D
【解析】如图所示,取 的中点 ,连接 ,,
则 ,,
所以 .
在 中,有 ,
所以 .
第二部分
11. 相交或平行
【解析】
, 可以是平行的,当 ,,, 位于如图所示的位置时,可知 , 相交.
12.
【解析】如图,取 的中点 ,连接 ,.
易知 ,,,
故 ,
所以 .
因为 ,,,
则 .
同理 .
又 , 分别为 , 的中点,
则 , 也为 , 的中点,
从而得 ,
所以四边形 为平行四边形.
又 ,,,
所以 ,
所以四边形 为矩形,
其面积 .
13. ,
【解析】因为 ,
所以 ,即 ,
所以 ,.
14. 平行,异面,相交,异面
15.
【解析】①体现的是线面平行的判定定理,缺的条件是“ 为 外的直线”即“”,它同样也适合②③.
第三部分
16. 如图所示,在 上取一点 ,使 ,
则易知 ,且 ,
所以四边形 为平行四边形,
所以 ,且 .
又因为 ,且 ,
,且 ,
所以 ,且
所以四边形 是平行四边形,
所以 ,.
又因为 ,,
所以四边形 是平行四边形,
所以 ,.
所以 ,,
所以四边形 是平行四边形.
17. (1) 连接 ,
因为 ,, 是 的中点,
所以 ,,
所以四边形 是平行四边形,
所以 为 的中点.
又因为 是 的中点,
所以 .
因为 ,,
所以 .
(2) 连接 ,,
因为 , 分别是 , 的中点,
所以 .
因为 ,,
所以 .
又因为 是 的中点, 是 的中点,
所以 .
又因为 ,,
所以 .
又因为 ,
所以平面 .
又因为 ,
所以 .
18. 要证明线线平行,可考虑先找线面平行,再利用线面平行的性质定理证明线线平行.
在正方形 中,因为 是 的中点,
所以 .
又 ,,
所以 .
又因为 且 ,
所以 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. ,点 ,,点 ,,则能得到直线 直线 的是
A. B.
C. 且相交 D. ,,, 四点共面
2. 若平面 平面 ,则
A. 平面 内任一条直线与平面 平行
B. 平面 内任一条直线与平面 内任一条直线平行
C. 平面 内存在一条直线与平面 不平行
D. 平面 内一条直线与平面 内一条直线有可能相交
3. 已知 是 所在平面外一点,, 交线段 ,, 于点 ,,,若 ,则 等于
A. B. C. D.
4. 平面 ,, 分别在 、 内,线段 ,, 共点于 , 在 、 之间.若 ,,,,则 的面积为
A. B. C. D.
5. 为矩形 所在平面外一点,矩形对角线交点为 , 为 的中点,给出四个结论:① ;② ;③ ;④ ;⑤ ,其中正确的个数有
A. B. C. D.
6. 下列说法中,正确的是
A. 空间中没有交点的两条直线是平行直线
B. 一条直线和两条平行直线中的一条相交,则它和另一条直线也相交
C. 空间四条直线 ,,,,若 , 且 ,则
D. 分别在两个平面内的直线是平行直线
7. 如图,在长方体 中,,,,点 是棱 的中点,点 在棱 上,且满足 , 是侧面四边形 内一动点(含边界),若 ,则线段 长度的取值范围是
A. B. C. D.
8. 如图,,, 分别为正方体对应棱的中点,则平面 与平面 的位置关系是
A. 垂直 B. 相交不垂直 C. 平行 D. 重合
9. 如图所示,下列四个正方体图形中,, 为正方体的两个顶点,,, 分别为其所在棱的中点,能得出 的图形序号是
A. ①③ B. ①④ C. ②③ D. ②④
10. 如图所示,已知三棱锥 中,, 分别为 , 的中点,则下列结论正确的是
A. B.
C. D.
二、填空题(共5小题;共25分)
11. 直线 ,,平面 , 满足 ,,,则平面 , 的位置关系是 .
12. 在三棱锥 中, 是边长为 的正三角形,,平面 分别与 ,,, 交于点 ,,,., 分别是 , 的中点,如果 ,那么四边形 的面积为 .
13. 夹在两平行平面间的两条线段 , 相交于 (如图所示),已知 ,,.则线段 , 的长分别为 .
14. 如图所示,正方体 中,判断下列直线的位置关系:
(1)直线 与直线 的位置关系是 ;
(2)直线 与直线 的位置关系是 ;
(3)直线 与直线 的位置关系是 ;
(4)直线 与直线 的位置关系是 .
15. 考察下列三个命题:“”处都缺少同一个条件,补上这个条件使其构成真命题(其中 , 为直线,, 为平面),则此条件为 .
① ;② ;③ ;
三、解答题(共3小题;共39分)
16. 已知 和 分别是正方体 的棱 和棱 上的点,且 ,求证:四边形 是平行四边形.
17. 如图,四棱锥 中,,,,, 分别是线段 ,, 的中点, 与 交于 点, 是线段 上一点.求证:
(1);
(2).
18. 如图,正方形 中,, 分别为 , 的中点.在五棱锥 中, 为棱 的中点,平面 与棱 , 分别交于点 ,.求证:.
答案
第一部分
1. D 【解析】若 ,,, 四点共面,则直线 是平面 与平面 的交线,直线 是平面 与平面 的交线,由线面平行的性质得 .
2. A
3. B 【解析】由题意,,由相似三角形中面积比等于边长比的平方得 .
4. C 【解析】如图,因为 ,所以 ,,,
所以 ,
且由 知相似比为 ,
又由 ,,,
知 ,
所以 .
5. C
【解析】由题意知 ,则 ,且 .
6. C
7. A
8. C 【解析】如图,分别取另三条棱的中点 ,,,将平面 延展为平面正六边形 ,
因为 ,,且 与 相交, 与 相交,
所以 ,即 .
9. B 【解析】利用线面平行的定义判定.
10. D
【解析】如图所示,取 的中点 ,连接 ,,
则 ,,
所以 .
在 中,有 ,
所以 .
第二部分
11. 相交或平行
【解析】
, 可以是平行的,当 ,,, 位于如图所示的位置时,可知 , 相交.
12.
【解析】如图,取 的中点 ,连接 ,.
易知 ,,,
故 ,
所以 .
因为 ,,,
则 .
同理 .
又 , 分别为 , 的中点,
则 , 也为 , 的中点,
从而得 ,
所以四边形 为平行四边形.
又 ,,,
所以 ,
所以四边形 为矩形,
其面积 .
13. ,
【解析】因为 ,
所以 ,即 ,
所以 ,.
14. 平行,异面,相交,异面
15.
【解析】①体现的是线面平行的判定定理,缺的条件是“ 为 外的直线”即“”,它同样也适合②③.
第三部分
16. 如图所示,在 上取一点 ,使 ,
则易知 ,且 ,
所以四边形 为平行四边形,
所以 ,且 .
又因为 ,且 ,
,且 ,
所以 ,且
所以四边形 是平行四边形,
所以 ,.
又因为 ,,
所以四边形 是平行四边形,
所以 ,.
所以 ,,
所以四边形 是平行四边形.
17. (1) 连接 ,
因为 ,, 是 的中点,
所以 ,,
所以四边形 是平行四边形,
所以 为 的中点.
又因为 是 的中点,
所以 .
因为 ,,
所以 .
(2) 连接 ,,
因为 , 分别是 , 的中点,
所以 .
因为 ,,
所以 .
又因为 是 的中点, 是 的中点,
所以 .
又因为 ,,
所以 .
又因为 ,
所以平面 .
又因为 ,
所以 .
18. 要证明线线平行,可考虑先找线面平行,再利用线面平行的性质定理证明线线平行.
在正方形 中,因为 是 的中点,
所以 .
又 ,,
所以 .
又因为 且 ,
所以 .
第1页(共1 页)
