2.2 用样本估计总体(Word含答案)
文档属性
| 名称 | 2.2 用样本估计总体(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 191.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览


文档简介
2.2 用样本估计总体
一、选择题(共10小题;共50分)
1. 在 年第 届北京奥运会上,我国代表团的金牌数雄踞榜首.如图是位居金牌榜前十二位的代表团获得的金牌数的茎叶图,则这十二个代表团获得的金牌数的平均数与中位数的差 的值为
A. B. C. D.
2. 为了研究某药品的疗效,选取若干名志愿者进行临床试验所有志愿者的舒张压数据(单位:)的分组区间为 ,,,,,将其按从左到右的顺序分别编号为第一组,第二组,,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有 人,第三组中没有疗效的有 人,则第三组中有疗效的人数为
A. B. C. D.
3. 在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续 天,每天新增疑似病例不超过 人”.根据过去 天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为 ,中位数为
B. 乙地:总体均值为 ,总体方差大于
C. 丙地:中位数为 ,众数为
D. 丁地:总体均值为 ,总体方差为
4. 为全面地了解学生对任课教师教学的满意程度,特在某班开展教学调查.采用简单随机抽样的办法,从该班抽取 名学生,根据他们对语文、数学教师教学的满意度评分(百分制),绘制茎叶图如图.设该班学生对语文、数学教师教学的满意度评分的中位数分别为 ,,则
A. B. C. D. 无法确定
5. 在如图所示的“茎叶图”表示的数据中,众数和中位数分别
A. 与 B. 与 C. 与 D. 与
6. 某书店新进了一批书籍,如表是某月中连续 天的销售情况记录:
根据上表估计该书店该月(按 天计算)的销售总量是
A. 本 B. 本 C. 本 D. 本
7. 如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是
A. , B. , C. , D. ,
8. 已知数据 ,,,,,(单位:公斤),其中 ,,,, 是某班 个学生的体重,设这 个学生体重的平均数为 ,中位数为 ,则 ,,,,, 这 个数据的平均数、中位数分别与 , 比较,下列说法正确的是
A. 平均数增大,中位数一定变大 B. 平均数增大,中位数可能不变
C. 平均数可能不变,中位数可能不变 D. 平均数可能不变,中位数可能变小
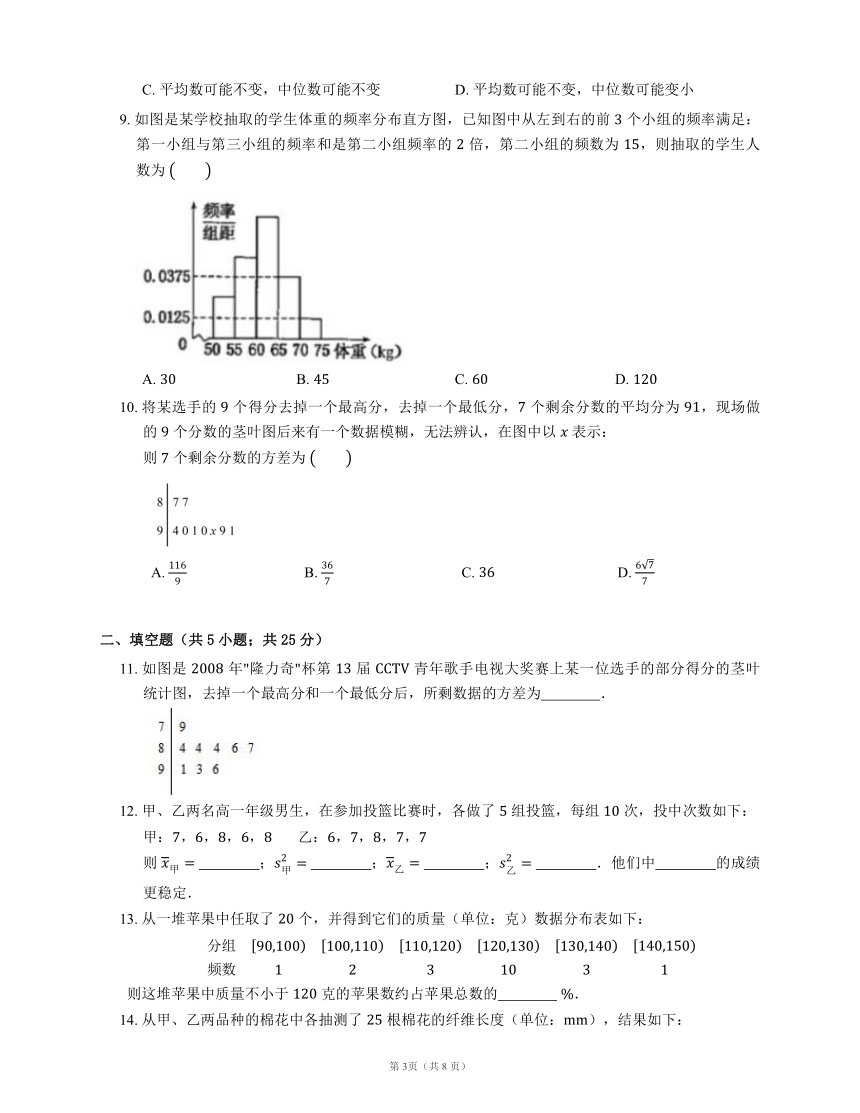
9. 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前 个小组的频率满足:第一小组与第三小组的频率和是第二小组频率的 倍,第二小组的频数为 ,则抽取的学生人数为
A. B. C. D.
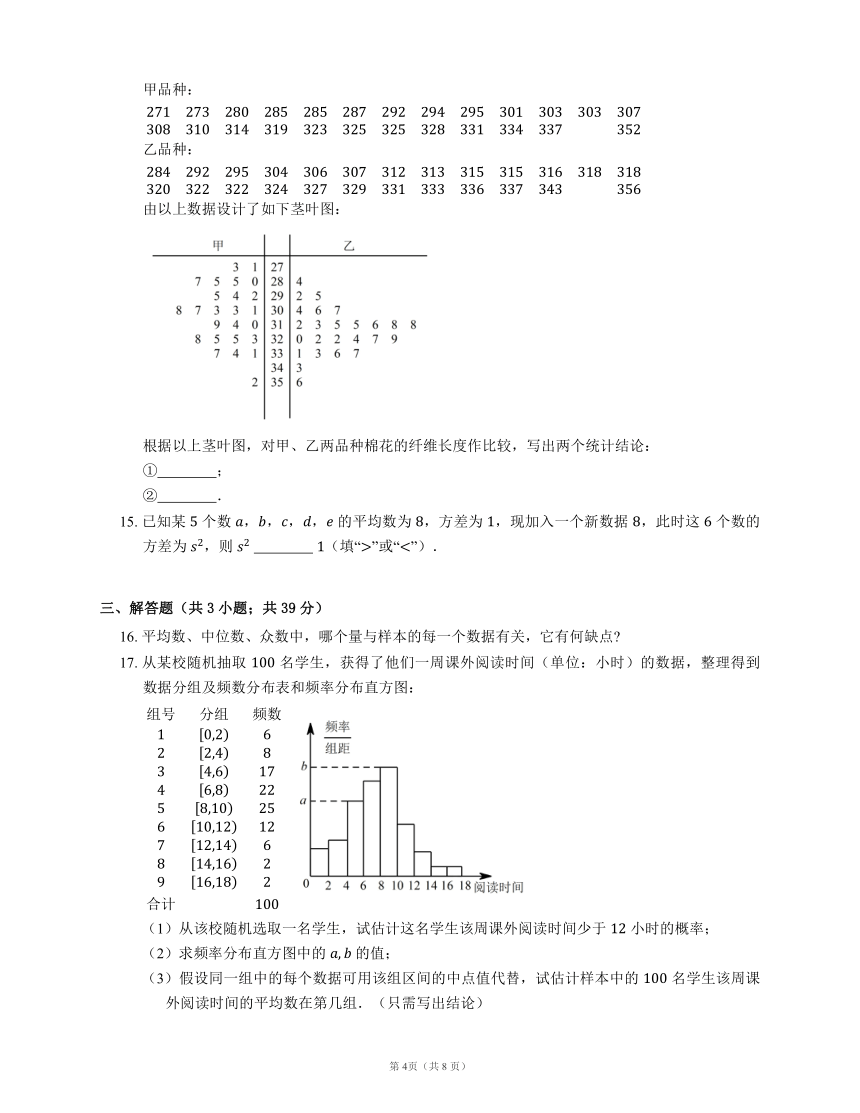
10. 将某选手的 个得分去掉一个最高分,去掉一个最低分, 个剩余分数的平均分为 ,现场做的 个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以 表示:
则 个剩余分数的方差为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如图是 年"隆力奇"杯第 届 青年歌手电视大奖赛上某一位选手的部分得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为 .
12. 甲、乙两名高一年级男生,在参加投篮比赛时,各做了 组投篮,每组 次,投中次数如下:
甲:,,,, 乙:,,,,
则 ; ; ; .他们中 的成绩更稳定.
13. 从一堆苹果中任取了 个,并得到它们的质量(单位:克)数据分布表如下:
则这堆苹果中质量不小于 克的苹果数约占苹果总数的 .
14. 从甲、乙两品种的棉花中各抽测了 根棉花的纤维长度(单位:),结果如下:
甲品种:
乙品种:
由以上数据设计了如下茎叶图:
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
① ;
② .
15. 已知某 个数 ,,,, 的平均数为 ,方差为 ,现加入一个新数据 ,此时这 个数的方差为 ,则 (填“”或“”).
三、解答题(共3小题;共39分)
16. 平均数、中位数、众数中,哪个量与样本的每一个数据有关,它有何缺点
17. 从某校随机抽取 名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于 小时的概率;
(2)求频率分布直方图中的 的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的 名学生该周课外阅读时间的平均数在第几组.(只需写出结论)
18. 某篮球运动员的投篮命中率为 ,他想提高自己的投篮水平,制订了一个夏季训练计划.为了了解训练效果,执行计划前他统计了 场比赛的得分,计算出得分的中位数为 分,平均得分为 分,得分的方差为 .执行计划后也统计了 场比赛的得分,成绩的茎叶图如图所示:
(1)请计算该篮球运动员执行计划后统计的 场比赛得分的中位数、平均数与方差;
(2)如果仅从执行计划前后统计的各 场比赛得分数据分析,训练计划对该运动员的投篮水平的提高是否有帮助 请说明理由.
答案
第一部分
1. B 【解析】提示:平均数为 ,中位数为 .
2. C 【解析】由题可知,第一组与第二组共有 人,由直方图可得,分布在区间第一组与第二组的频率分别为 ,,
所以第一组有 人,第二组 人,第三组的频率为 ,
所以第三组的人数为 人,第三组中没有疗效的有 人,
所以第三组中有疗效的有 人.
3. D 【解析】根据信息可知,连续 天内,每天的新增疑似病例不能有超过 的数,选项 A 中,中位数为 ,可能存在大于 的数;
同理,在选项 C 中也有可能;
选项 B 中,如果某天数据为 ,其余 天为 ,则不符合标志;
选项 D 中,根据公式,若有大于 的数存在,则方差至少为 .
4. A 【解析】由茎叶图得 ,,
所以 .
5. D
6. A 【解析】从表中 天的销售情况可得,一天的平均销售量为 (本)
该月共 天,故该月的销售总量约为 (本).
7. D 【解析】第一个小矩形的面积为 ,第二个小矩形的面积为 ,因为频率分布直方图所有矩形的面积之和为 ,所以第三个小矩形的面积为 ,
平均数为 .
设中位数为 ,则 ,解得 .
8. B 【解析】由题意,显然该班 个学生体重的平均数 ,所以这 个数据的平均数 .而中位数可能不变.
9. C 【解析】第二小组的频率为 ;
则抽取的学生人数为 .
10. B
【解析】由茎叶图可知,该选手的最低分是 ,最高分是 ,
由题意得 ,解得 .
这 个剩余分数的方差 .
第二部分
11.
12. ,,,,乙
13.
【解析】由表中可知这堆苹果中,质量不小于 克的苹果数为 ,故约占苹果总数的 ,即 .
14. 乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度;
甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散(或乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中),甲品种棉花的纤维长度的中位数为 ,乙品种棉花的纤维长度的中位数为 ;
乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近),甲品种棉花的纤维长度除一个特殊值()外,也大致对称,其分布较均匀
15.
【解析】根据题意,某 个数 ,,,, 的平均数为 ,
则有 ,即 ,其方差为 ,
则有
即 ,
现加入一个新数据 ,数据变为:,,,,,;
其平均数 ,其方差
则有 .
第三部分
16. 平均数与样本的每一个数据有关,它可以反映出更多的关于样本数据总体的信息,但是平均数受数据中极端值的影响较大.
17. (1) 根据频数分布表, 名学生中课外阅读时间不少于 小时的学生共有 名,所以样本中的学生课外阅读时间少于 小时的频率是
从该校随机选取一名学生,估计这名学生该周课外阅读时间少于 小时的概率为 .
(2) 课外阅读时间落在组 的有 人,频率为 ,所以
课外阅读时间落在组 的有 人,频率为 ,所以
(3) 估计样本中的 名学生课外阅读时间的平均数在第 组.
18. (1) 训练后得分的中位数为 (分);
平均得分为 (分);
方差为
(2) 有帮助.理由:尽管中位数训练后比训练前稍小,但平均得分一样,训练后方差小于训练前方差,说明训练后得分稳定性提高了,这是投篮水平提高表现,故此训练计划对该篮球运员的投篮水平的提高有帮助.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 在 年第 届北京奥运会上,我国代表团的金牌数雄踞榜首.如图是位居金牌榜前十二位的代表团获得的金牌数的茎叶图,则这十二个代表团获得的金牌数的平均数与中位数的差 的值为
A. B. C. D.
2. 为了研究某药品的疗效,选取若干名志愿者进行临床试验所有志愿者的舒张压数据(单位:)的分组区间为 ,,,,,将其按从左到右的顺序分别编号为第一组,第二组,,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有 人,第三组中没有疗效的有 人,则第三组中有疗效的人数为
A. B. C. D.
3. 在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续 天,每天新增疑似病例不超过 人”.根据过去 天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为 ,中位数为
B. 乙地:总体均值为 ,总体方差大于
C. 丙地:中位数为 ,众数为
D. 丁地:总体均值为 ,总体方差为
4. 为全面地了解学生对任课教师教学的满意程度,特在某班开展教学调查.采用简单随机抽样的办法,从该班抽取 名学生,根据他们对语文、数学教师教学的满意度评分(百分制),绘制茎叶图如图.设该班学生对语文、数学教师教学的满意度评分的中位数分别为 ,,则
A. B. C. D. 无法确定
5. 在如图所示的“茎叶图”表示的数据中,众数和中位数分别
A. 与 B. 与 C. 与 D. 与
6. 某书店新进了一批书籍,如表是某月中连续 天的销售情况记录:
根据上表估计该书店该月(按 天计算)的销售总量是
A. 本 B. 本 C. 本 D. 本
7. 如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是
A. , B. , C. , D. ,
8. 已知数据 ,,,,,(单位:公斤),其中 ,,,, 是某班 个学生的体重,设这 个学生体重的平均数为 ,中位数为 ,则 ,,,,, 这 个数据的平均数、中位数分别与 , 比较,下列说法正确的是
A. 平均数增大,中位数一定变大 B. 平均数增大,中位数可能不变
C. 平均数可能不变,中位数可能不变 D. 平均数可能不变,中位数可能变小
9. 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前 个小组的频率满足:第一小组与第三小组的频率和是第二小组频率的 倍,第二小组的频数为 ,则抽取的学生人数为
A. B. C. D.
10. 将某选手的 个得分去掉一个最高分,去掉一个最低分, 个剩余分数的平均分为 ,现场做的 个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以 表示:
则 个剩余分数的方差为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 如图是 年"隆力奇"杯第 届 青年歌手电视大奖赛上某一位选手的部分得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为 .
12. 甲、乙两名高一年级男生,在参加投篮比赛时,各做了 组投篮,每组 次,投中次数如下:
甲:,,,, 乙:,,,,
则 ; ; ; .他们中 的成绩更稳定.
13. 从一堆苹果中任取了 个,并得到它们的质量(单位:克)数据分布表如下:
则这堆苹果中质量不小于 克的苹果数约占苹果总数的 .
14. 从甲、乙两品种的棉花中各抽测了 根棉花的纤维长度(单位:),结果如下:
甲品种:
乙品种:
由以上数据设计了如下茎叶图:
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
① ;
② .
15. 已知某 个数 ,,,, 的平均数为 ,方差为 ,现加入一个新数据 ,此时这 个数的方差为 ,则 (填“”或“”).
三、解答题(共3小题;共39分)
16. 平均数、中位数、众数中,哪个量与样本的每一个数据有关,它有何缺点
17. 从某校随机抽取 名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于 小时的概率;
(2)求频率分布直方图中的 的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的 名学生该周课外阅读时间的平均数在第几组.(只需写出结论)
18. 某篮球运动员的投篮命中率为 ,他想提高自己的投篮水平,制订了一个夏季训练计划.为了了解训练效果,执行计划前他统计了 场比赛的得分,计算出得分的中位数为 分,平均得分为 分,得分的方差为 .执行计划后也统计了 场比赛的得分,成绩的茎叶图如图所示:
(1)请计算该篮球运动员执行计划后统计的 场比赛得分的中位数、平均数与方差;
(2)如果仅从执行计划前后统计的各 场比赛得分数据分析,训练计划对该运动员的投篮水平的提高是否有帮助 请说明理由.
答案
第一部分
1. B 【解析】提示:平均数为 ,中位数为 .
2. C 【解析】由题可知,第一组与第二组共有 人,由直方图可得,分布在区间第一组与第二组的频率分别为 ,,
所以第一组有 人,第二组 人,第三组的频率为 ,
所以第三组的人数为 人,第三组中没有疗效的有 人,
所以第三组中有疗效的有 人.
3. D 【解析】根据信息可知,连续 天内,每天的新增疑似病例不能有超过 的数,选项 A 中,中位数为 ,可能存在大于 的数;
同理,在选项 C 中也有可能;
选项 B 中,如果某天数据为 ,其余 天为 ,则不符合标志;
选项 D 中,根据公式,若有大于 的数存在,则方差至少为 .
4. A 【解析】由茎叶图得 ,,
所以 .
5. D
6. A 【解析】从表中 天的销售情况可得,一天的平均销售量为 (本)
该月共 天,故该月的销售总量约为 (本).
7. D 【解析】第一个小矩形的面积为 ,第二个小矩形的面积为 ,因为频率分布直方图所有矩形的面积之和为 ,所以第三个小矩形的面积为 ,
平均数为 .
设中位数为 ,则 ,解得 .
8. B 【解析】由题意,显然该班 个学生体重的平均数 ,所以这 个数据的平均数 .而中位数可能不变.
9. C 【解析】第二小组的频率为 ;
则抽取的学生人数为 .
10. B
【解析】由茎叶图可知,该选手的最低分是 ,最高分是 ,
由题意得 ,解得 .
这 个剩余分数的方差 .
第二部分
11.
12. ,,,,乙
13.
【解析】由表中可知这堆苹果中,质量不小于 克的苹果数为 ,故约占苹果总数的 ,即 .
14. 乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度;
甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散(或乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中),甲品种棉花的纤维长度的中位数为 ,乙品种棉花的纤维长度的中位数为 ;
乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近),甲品种棉花的纤维长度除一个特殊值()外,也大致对称,其分布较均匀
15.
【解析】根据题意,某 个数 ,,,, 的平均数为 ,
则有 ,即 ,其方差为 ,
则有
即 ,
现加入一个新数据 ,数据变为:,,,,,;
其平均数 ,其方差
则有 .
第三部分
16. 平均数与样本的每一个数据有关,它可以反映出更多的关于样本数据总体的信息,但是平均数受数据中极端值的影响较大.
17. (1) 根据频数分布表, 名学生中课外阅读时间不少于 小时的学生共有 名,所以样本中的学生课外阅读时间少于 小时的频率是
从该校随机选取一名学生,估计这名学生该周课外阅读时间少于 小时的概率为 .
(2) 课外阅读时间落在组 的有 人,频率为 ,所以
课外阅读时间落在组 的有 人,频率为 ,所以
(3) 估计样本中的 名学生课外阅读时间的平均数在第 组.
18. (1) 训练后得分的中位数为 (分);
平均得分为 (分);
方差为
(2) 有帮助.理由:尽管中位数训练后比训练前稍小,但平均得分一样,训练后方差小于训练前方差,说明训练后得分稳定性提高了,这是投篮水平提高表现,故此训练计划对该篮球运员的投篮水平的提高有帮助.
第1页(共1 页)
