上海市浦东新区2021-2022学年高二上学期期末质量测试数学试题(Word版含答案)
文档属性
| 名称 | 上海市浦东新区2021-2022学年高二上学期期末质量测试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 13:58:13 | ||
图片预览




文档简介
浦东新区2021-2022学年高二上学期期末质量测试数学试卷 2021年12月
考生注意:
1、答卷时间90分钟,满分100分;
2、请在答题纸上规定的地方作答,写在其它地方一律不予批阅.
一、填空题(本大题满分36分)本大题共有12题,只要求直接填写结果,每个空格填对得3分,否则一律得零分.
1.已知定直线,定点,则直线与点确定的平面有 个(请填写个数).
2. 已知球的半径为1,则此球的表面积为 .
3. 在装有4个红球和2个白球的盒子中任意取一球,则 “取出的球是白球”为 现象(填“随机”或“确定性”).
4. 已知随机事件A和B不可能同时发生,若,,则 .
5. 我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 .
6. “若直线平面,则直线与平面内无数条直线垂直”是 命题.(请用“真”,“假”填空)
7. 已知正三棱锥的底面边长为4,高为2,则此三棱锥的体积为
8. 2021年7月24日,在东京奥运会女子10米气步枪决赛中,中国选手杨倩以251.8环的总成绩夺得金牌,为中国代表团摘得本届奥运会首金.已知杨倩其中5次射击命中的环数如下:10.8,10.6,10.6,10.7,9.8,则这组数据的方差为 .
9. 作直线和平面,则下列小组内两个事件互为对立事件的有 组(请填写个数)A组:“”和“”;B组:“为异面直线”和“”;
C组:“或”和“与相交”.
10. 已知随机事件发生的概率满足,小华猜测事件会发生,小明猜测事件不会发生;则以下判断中正确的是 .(请填写序号)
①小华一定猜错;②小华和小明猜对的可能性一样大;③小明猜对的可能性更大;④无法判断小华和小明谁猜对的可能性更大.
11. 已知棱长为4的正方体,动点M在正方体表面上,且满足,则以下结论中正确的是: (请填写序号)
①满足条件的点M有且只有6个;②满足条件的点M都在同一个平面上;
③点M的轨迹长度为.
12. 如图,在中,已知,D是斜边AB上任意一点(不含端点)沿直线CD将折成直二面角,当 时,折叠后A、B两点间的距离最小.
二、选择题(本大题满分12分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,每题答对得3分,否则一律得零分.
13.下列调查方式合适的是( )
A.为了了解一批炮弹的杀伤半径,采用普查的方式
B.为了了解一批玉米种子的发芽率,采用普查的方式
C.为了了解一条河流的水质,采用抽查的方式
D.为了了解一个寝室的学生(共5个人)每周体育锻炼的时间,采用抽查的方式
14.如果一个角的两边和另一个角的两边分别平行,那么这两个角( )
A.相等 B.互补 C.相等或互补 D.互余
15.军训时,甲、乙两名同学进行射击比赛,共比赛10场,每场比赛各射击四次,且用每场击中环数之和作为该场比赛的成绩.数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图,并给出下列三个结论:
(1)甲的成绩的极差是29;
(2)乙的成绩的众数是21;
(3)乙的成绩的中位数是18.
则这三个结论中,错误结论的个数为( )
A.0 B.1 C.2 D.3
16.投壶是我国古代的一种娱乐活动,比赛投中得分情况分“有初”,“贯耳”,“散射”,“双耳”,“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为,投中“贯耳”的概率为,投中“散射”的概率为,投中“双耳”的概率为,投中“依竿”的概率为,未投中(筹)的概率为.乙的投掷水平与甲相同,且甲、乙投掷相互独立.比赛第一场,两人平局;第二场甲投中“有初”,乙投中“双耳”,则三场比赛结束时,甲获胜的概率为( )
A. B. C. D.
三、解答题(本大题满分52分)本大题共有5题,解答下列各题必须写出必要的步骤.
17.(本题满分10分)独立地重复抛掷硬币2次,若每次抛掷硬币正面朝上和反面朝上的概率都是0.5,回答以下两个问题:
(1)现将“独立地重复抛掷硬币2次”作为一次试验,若用分别表示正面朝上和反面朝上,例如用表示某次试验的结果是第一次正面朝上,第二次反面朝上,请用符号写出“独立地重复抛掷硬币2次”的样本空间;
(2)已知在某次试验中第一次抛掷的结果是正面朝上;某同学说“第二次抛掷硬币正面朝上的可能性小于反面朝上的可能性”请问该同学的表述是否正确?(不需要写出理由)
解
18.(本题满分10分)已知某圆柱底面半径和母线长都是3.
(1)求出该圆柱的表面积和体积;
(2)若圆锥与该圆柱底面半径、高都相等,求圆锥的侧面积.
19.(本题满分10分)如图,在正方体中.
(1)求异面直线和所成的角的余弦值;
(2)求证:直线平面.
解:
解:
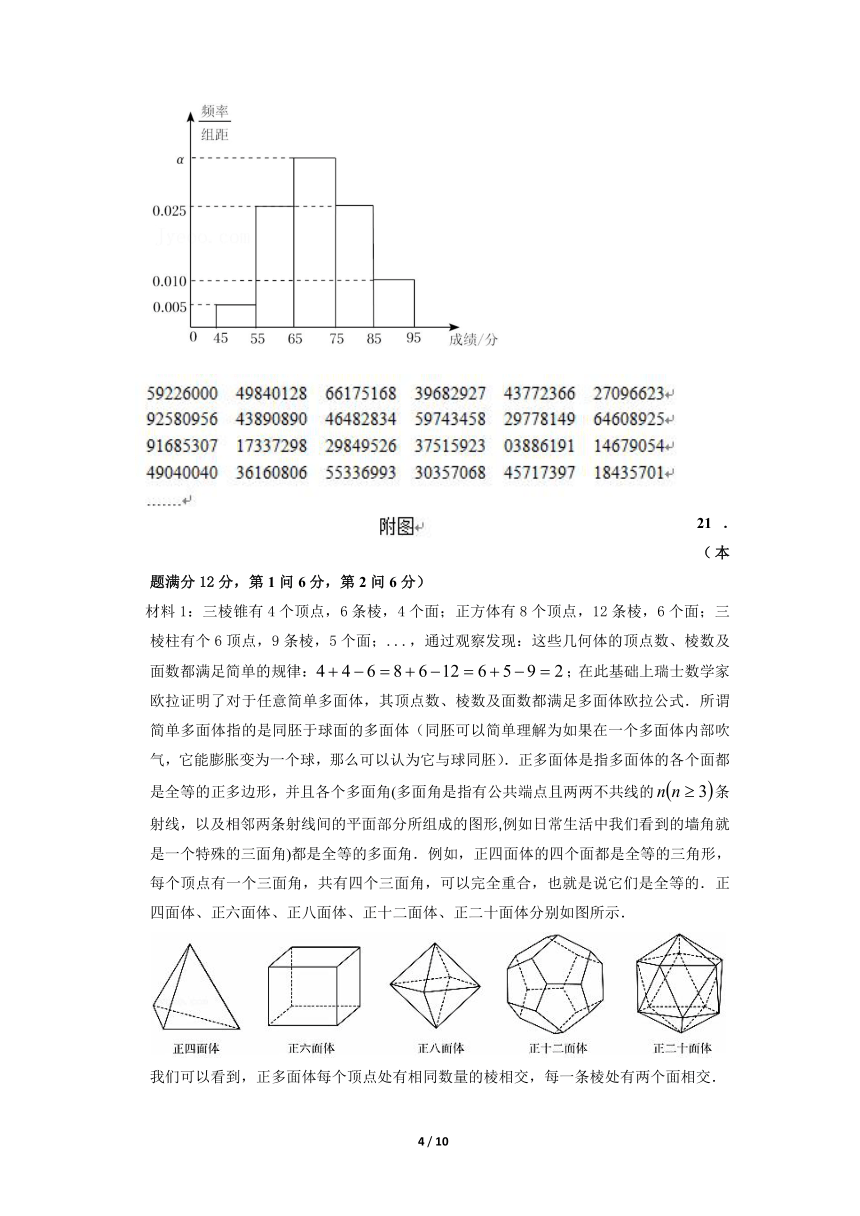
20.(本题满分10分)2020年1月8日,在“不忘初心、牢记使命”主题教育总结大会上,习总书记指出:“要把学习贯彻党的创新理论作为思想武装的重中之重,同学习党史、新中国史、改革开放史、社会主义发展史结合起来。”为了提高思想认识,某校开展了“学史明鉴、牢记使命”知识竞赛活动,从950名参赛的学生中随机选取100人的成绩作为样本,得到如图所示的频率分布直方图.
(1)现将全体参赛学生成绩编号为001--950,使用附图提供的“随机数表”从第二行的第三个数开始从左往右抽,请写出前3个被抽到样本编号;
(2)求频率分布直方图中的值,并估计该校此次参赛学生成绩的平均分(同一组数据用该组区间的中点值代表).
21.(本题满分12分,第1问6分,第2问6分)
材料1:三棱锥有4个顶点,6条棱,4个面;正方体有8个顶点,12条棱,6个面;三棱柱有个6顶点,9条棱,5个面;...,通过观察发现:这些几何体的顶点数、棱数及面数都满足简单的规律:;在此基础上瑞士数学家欧拉证明了对于任意简单多面体,其顶点数、棱数及面数都满足多面体欧拉公式.所谓简单多面体指的是同胚于球面的多面体(同胚可以简单理解为如果在一个多面体内部吹气,它能膨胀变为一个球,那么可以认为它与球同胚).正多面体是指多面体的各个面都是全等的正多边形,并且各个多面角(多面角是指有公共端点且两两不共线的条射线,以及相邻两条射线间的平面部分所组成的图形,例如日常生活中我们看到的墙角就是一个特殊的三面角)都是全等的多面角.例如,正四面体的四个面都是全等的三角形,每个顶点有一个三面角,共有四个三面角,可以完全重合,也就是说它们是全等的.正四面体、正六面体、正八面体、正十二面体、正二十面体分别如图所示.
我们可以看到,正多面体每个顶点处有相同数量的棱相交,每一条棱处有两个面相交.
材料2:1996年诺贝尔化学奖授予对发现C60有重大贡献的三位科学家,C60是由60个C原子构成的分子,它是形如足球的多面体,这个多面体有60个顶点,以每一个顶点为端点都有三条棱,面的形状只有五边形和六边形;
(1)阅读上述材料,请用数学符号表示简单多面体的顶点数、棱数及面数,并用相应的数学符号写出多面体欧拉公式(不需要证明);
(2)请结合上述材料,在下面两个问题中选择一个回答,并写出解答过程. (选择问题1分,解答过程正确5分;两个问题都选择,不给分)
问题1:请问C60的分子结构模型中,有几个五边形?
问题2:简单多面体中是否存在正16面体?如果存在请作出它的大致图形并指出面的形状;如果不存在,请说明理由.
参考答案
一、填空题(本大题满分36分)本大题共有12题,只要求直接填写结果,每个空格填对得3分,否则一律得零分.
1.已知定直线,定点,则直线与点确定的平面有 1 个(请填写个数).
2. 已知球的半径为1,则此球的表面积为 .
3. 在装有4个红球和2个白球的盒子中任意取一球,则 “取出的球是白球”为 随机 现象(填“随机”或“确定性”).
4. 已知随机事件A和B不可能同时发生,若,,则P(B)= .
5. 我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 0.98 .
6. “若直线平面,则直线与平面内无数条直线垂直”是 真 命题.(请用“真”,“假”填空)
7. 已知正三棱锥的底面边长为4,高为2,则此三棱锥的体积为
8. 2021年7月24日,在东京奥运会女子10米气步枪决赛中,中国选手杨倩以251.8环的总成绩夺得金牌,为中国代表团摘得本届奥运会首金.已知杨倩其中5次射击命中的环数如下:10.8,10.6,10.6,10.7,9.8,则这组数据的方差为 0.128 .
9. 作直线和平面,则下列小组内两个事件互为对立事件的有 1 组(请填写个数)A组:“”和“”;B组:“为异面直线”和“”;
C组:“或”和“与相交”.
10. 已知随机事件发生的概率满足,小华猜测事件会发生,小明猜测事件不会发生;则以下判读中正确的是 ③ .(请填写序号)
①小华一定猜错;②小华和小明猜对的可能性一样大;③小明猜对的可能性更大;④无法判断小华和小明谁猜对的可能性更大.
11. 已知棱长为4的正方体,动点M在正方体表面上,且满足,则以下结论中正确的是: ② ③ (请填写序号)
①满足条件的点M有且只有6个;②满足条件的点M都在同一个平面上;
③点M的轨迹长度为.
12. 如图,在中,已知,D是斜边AB上任意一点(不含端点)沿直线CD将折成直二面角,当 时,折叠后A、B两点间的距离最小.
二、选择题(本大题满分12分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,每题答对得3分,否则一律得零分.
13.下列调查方式合适的是( C )
A.为了了解一批炮弹的杀伤半径,采用普查的方式
B.为了了解一批玉米种子的发芽率,采用普查的方式
C.为了了解一条河流的水质,采用抽查的方式
D.为了了解一个寝室的学生(共5个人)每周体育锻炼的时间,采用抽查的方式
14.空间中,如果一个角的两边和另一个角的两边分别对应平行,那么这两个角( C )
A.相等 B.互补 C.相等或互补 D.互余
15.军训时,甲、乙两名同学进行射击比赛,共比赛10场,每场比赛各射击四次,且用每场击中环数之和作为该场比赛的成绩.数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图,并给出下列三个结论:
(1)甲的成绩的极差是29;
(2)乙的成绩的众数是21;
(3)乙的成绩的中位数是18.
则这三个结论中,错误结论的个数为(B )
A.0 B.1 C.2 D.3
16.投壶是我国古代的一种娱乐活动,比赛投中得分情况分“有初”,“贯耳”,“散射”,“双耳”,“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为,投中“贯耳”的概率为,投中“散射”的概率为,投中“双耳”的概率为,投中“依竿”的概率为,未投中(筹)的概率为.乙的投掷水平与甲相同,且甲、乙投掷相互独立.比赛第一场,两人平局;第二场甲投中“有初”,乙投中“双耳”,则三场比赛结束时,甲获胜的概率为( A )
A. B. C. D.
三、解答题(本大题满分52分)本大题共有5题,解答下列各题必须写出必要的步骤.
17.(本题满分10分)独立地重复抛掷硬币2次,若每次抛掷硬币正面朝上和反面朝上的概率都是0.5,回答以下两个问题:
(1)现将“独立地重复抛掷硬币2次”作为一次试验,若用分别表示正面朝上和反面朝上,例如用表示某次试验的结果是第一次正面朝上,第二次反面朝上,请用符号写出“独立地重复抛掷硬币2次”的样本空间;
(2)已知在某次试验中第一次抛掷的结果是正面朝上;某同学说“第二次抛掷硬币正面朝上的可能性小于反面朝上的可能性”请问该同学的表述是否正确?(不需要写出理由)
解:(1)
说明:本题6分,如果没有写集合但是元素都表示正确的情况下建议给4分;其它情况题组长酌情处理;
不正确
说明:本题4分
18.(本题满分10分)已知某圆柱底面半径和母线长都是3.
(1)求出该圆柱的表面积和体积;
(2)若圆锥与该圆柱底面半径、高都相等,求圆锥的侧面积
解:(1);
说明:本题6分,面积和体积各3分;答案正确满分,答案不正确但公式正确每个2分;其它情况题组长酌情处理;
(2)
说明:本题4分;答案正确满分,答案不正确但公式正确2分;其它情况题组长酌情处理;
19.(本题满分10分)如图,在正方体中.
(1)求异面直线和所成的角的余弦值;
(2)求证:直线平面.
解:(1)因为,所以就是异面直线和所成的角或其补角.所以异面直线和所成的角为,所以异面直线和所成的角的余弦值为.
说明:本题5分,答案正确满分;答案不正确时找到角并表达正确给3分;题组长酌情处理;
(2)连接,因为,所以四边形为平行四边形,所以;在平面外,在平面内;所以直线平面
说明:本题5分;有辅助线作图或文字表述2分,得出“”2分,结论1分;其它情况题组长酌情处理;
20.(本题满分10分)2020年1月8日,在“不忘初心、牢记使命”主题教育总结大会上,习总书记指出:“要把学习贯彻党的创新理论作为思想武装的重中之重,同学习党史、新中国史、改革开放史、社会主义发展史结合起来。为了提高思想认识,某校开展了“学史明鉴、牢记使命”知识竞赛活动,从950名参赛的学生中随机选取100人的成绩作为样本,得到如图所示的频率分布直方图.
(1)现将全体参赛学生成绩编号为001--950,使用附图提供的“随机数表”从第二行的第三个数开始从左往右抽,请写出前3个被抽到样本编号;
(2)求频率分布直方图中的值,并估计该校此次参赛学生成绩的平均分(同一组数据用该组区间的中点值代表).
解:(1)580;438;908
说明:本题5分,写对1个给1分,写对2个给3分,全部写对给5分;顺序错了不扣分;其它情况题组长酌情处理;
(2);
说明:本题5分,写对给2分,写对给3分;其它情况题组长酌情处理;
21.(本题满分12分,第1问6分,第2问6分)
材料1:三棱锥有4个顶点,6条棱,4个面;正方体有8个顶点,12条棱,6个面;三棱柱有个6顶点,9条棱,5个面;...,通过观察发现:这些几何体的顶点数、棱数及面数都满足简单的规律:4+4-6=8+6-12=6+5-9=2;在此基础上瑞士数学家欧拉证明了对于任意简单多面体,其顶点数、棱数及面数都满足多面体欧拉公式.所谓简单多面体指的是同胚于球面的多面体(同胚可以简单理解为如果在一个多面体内部吹气,它能膨胀变为一个球,那么可以认为它与球同胚).正多面体是指多面体的各个面都是全等的正多边形,并且各个多面角(多面角是指有公共端点且两两不共线的条射线,以及相邻两条射线间的平面部分所组成的图形,例如日常生活中我们看到的墙角就是一个特殊的三面角)都是全等的多面角.例如,正四面体的四个面都是全等的三角形,每个顶点有一个三面角,共有四个三面角,可以完全重合,也就是说它们是全等的.正四面体、正六面体、正八面体、正十二面体、正二十面体分别如图所示.
我们可以看到,正多面体每个顶点处有相同数量的棱相交,每一条棱处有两个面相交.
材料2:1996年诺贝尔化学奖授予对发现C60有重大贡献的三位科学家,C60是由60个C原子构成的分子,它是形如足球的多面体,这个多面体有60个顶点,以每一个顶点为端点都有三条棱,面的形状只有五边形和六边形;
(1)阅读上述材料,请用数学符号表示简单多面体的顶点数、棱数及面数,并用相应的数学符号写出多面体欧拉公式(不需要证明);
(2)请结合上述材料,在下面两个问题中选择一个回答,并写出解答过程. (选择问题1分,解答过程正确5分;两个问题都选择,不给分)
问题1:请问C60的分子机构模型中,有几个五边形?
问题2:简单多面体中是否存在正16面体?如果存在请作出它的大致图形并指出面的形状;如果不存在,请说明理由.
解: (1)设多面体的顶点数为,棱数为,面数为;
则多面体欧拉公式为
说明:本题6分;具体给分方式题组长酌情处理;
(2)问题1:设C60的分子机构模型中,有个五边形, 个五边形
则: ,所以有12个五边形
问题2:设多面体的顶点数为,棱数为,面数为;每个面都是正边形,每个顶点为端点都有条棱.
则,
,不可能都大于4
时, 得 正四面体、正六面体、正十二面体
时, 得 正四面体、正八面体、正二十面体
说明:本题6分;如果两个都选了,按选第一个批改但如果回答错误,选题的1分不给;具体给分方式题组长酌情处理.
11 / 11
考生注意:
1、答卷时间90分钟,满分100分;
2、请在答题纸上规定的地方作答,写在其它地方一律不予批阅.
一、填空题(本大题满分36分)本大题共有12题,只要求直接填写结果,每个空格填对得3分,否则一律得零分.
1.已知定直线,定点,则直线与点确定的平面有 个(请填写个数).
2. 已知球的半径为1,则此球的表面积为 .
3. 在装有4个红球和2个白球的盒子中任意取一球,则 “取出的球是白球”为 现象(填“随机”或“确定性”).
4. 已知随机事件A和B不可能同时发生,若,,则 .
5. 我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 .
6. “若直线平面,则直线与平面内无数条直线垂直”是 命题.(请用“真”,“假”填空)
7. 已知正三棱锥的底面边长为4,高为2,则此三棱锥的体积为
8. 2021年7月24日,在东京奥运会女子10米气步枪决赛中,中国选手杨倩以251.8环的总成绩夺得金牌,为中国代表团摘得本届奥运会首金.已知杨倩其中5次射击命中的环数如下:10.8,10.6,10.6,10.7,9.8,则这组数据的方差为 .
9. 作直线和平面,则下列小组内两个事件互为对立事件的有 组(请填写个数)A组:“”和“”;B组:“为异面直线”和“”;
C组:“或”和“与相交”.
10. 已知随机事件发生的概率满足,小华猜测事件会发生,小明猜测事件不会发生;则以下判断中正确的是 .(请填写序号)
①小华一定猜错;②小华和小明猜对的可能性一样大;③小明猜对的可能性更大;④无法判断小华和小明谁猜对的可能性更大.
11. 已知棱长为4的正方体,动点M在正方体表面上,且满足,则以下结论中正确的是: (请填写序号)
①满足条件的点M有且只有6个;②满足条件的点M都在同一个平面上;
③点M的轨迹长度为.
12. 如图,在中,已知,D是斜边AB上任意一点(不含端点)沿直线CD将折成直二面角,当 时,折叠后A、B两点间的距离最小.
二、选择题(本大题满分12分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,每题答对得3分,否则一律得零分.
13.下列调查方式合适的是( )
A.为了了解一批炮弹的杀伤半径,采用普查的方式
B.为了了解一批玉米种子的发芽率,采用普查的方式
C.为了了解一条河流的水质,采用抽查的方式
D.为了了解一个寝室的学生(共5个人)每周体育锻炼的时间,采用抽查的方式
14.如果一个角的两边和另一个角的两边分别平行,那么这两个角( )
A.相等 B.互补 C.相等或互补 D.互余
15.军训时,甲、乙两名同学进行射击比赛,共比赛10场,每场比赛各射击四次,且用每场击中环数之和作为该场比赛的成绩.数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图,并给出下列三个结论:
(1)甲的成绩的极差是29;
(2)乙的成绩的众数是21;
(3)乙的成绩的中位数是18.
则这三个结论中,错误结论的个数为( )
A.0 B.1 C.2 D.3
16.投壶是我国古代的一种娱乐活动,比赛投中得分情况分“有初”,“贯耳”,“散射”,“双耳”,“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为,投中“贯耳”的概率为,投中“散射”的概率为,投中“双耳”的概率为,投中“依竿”的概率为,未投中(筹)的概率为.乙的投掷水平与甲相同,且甲、乙投掷相互独立.比赛第一场,两人平局;第二场甲投中“有初”,乙投中“双耳”,则三场比赛结束时,甲获胜的概率为( )
A. B. C. D.
三、解答题(本大题满分52分)本大题共有5题,解答下列各题必须写出必要的步骤.
17.(本题满分10分)独立地重复抛掷硬币2次,若每次抛掷硬币正面朝上和反面朝上的概率都是0.5,回答以下两个问题:
(1)现将“独立地重复抛掷硬币2次”作为一次试验,若用分别表示正面朝上和反面朝上,例如用表示某次试验的结果是第一次正面朝上,第二次反面朝上,请用符号写出“独立地重复抛掷硬币2次”的样本空间;
(2)已知在某次试验中第一次抛掷的结果是正面朝上;某同学说“第二次抛掷硬币正面朝上的可能性小于反面朝上的可能性”请问该同学的表述是否正确?(不需要写出理由)
解
18.(本题满分10分)已知某圆柱底面半径和母线长都是3.
(1)求出该圆柱的表面积和体积;
(2)若圆锥与该圆柱底面半径、高都相等,求圆锥的侧面积.
19.(本题满分10分)如图,在正方体中.
(1)求异面直线和所成的角的余弦值;
(2)求证:直线平面.
解:
解:
20.(本题满分10分)2020年1月8日,在“不忘初心、牢记使命”主题教育总结大会上,习总书记指出:“要把学习贯彻党的创新理论作为思想武装的重中之重,同学习党史、新中国史、改革开放史、社会主义发展史结合起来。”为了提高思想认识,某校开展了“学史明鉴、牢记使命”知识竞赛活动,从950名参赛的学生中随机选取100人的成绩作为样本,得到如图所示的频率分布直方图.
(1)现将全体参赛学生成绩编号为001--950,使用附图提供的“随机数表”从第二行的第三个数开始从左往右抽,请写出前3个被抽到样本编号;
(2)求频率分布直方图中的值,并估计该校此次参赛学生成绩的平均分(同一组数据用该组区间的中点值代表).
21.(本题满分12分,第1问6分,第2问6分)
材料1:三棱锥有4个顶点,6条棱,4个面;正方体有8个顶点,12条棱,6个面;三棱柱有个6顶点,9条棱,5个面;...,通过观察发现:这些几何体的顶点数、棱数及面数都满足简单的规律:;在此基础上瑞士数学家欧拉证明了对于任意简单多面体,其顶点数、棱数及面数都满足多面体欧拉公式.所谓简单多面体指的是同胚于球面的多面体(同胚可以简单理解为如果在一个多面体内部吹气,它能膨胀变为一个球,那么可以认为它与球同胚).正多面体是指多面体的各个面都是全等的正多边形,并且各个多面角(多面角是指有公共端点且两两不共线的条射线,以及相邻两条射线间的平面部分所组成的图形,例如日常生活中我们看到的墙角就是一个特殊的三面角)都是全等的多面角.例如,正四面体的四个面都是全等的三角形,每个顶点有一个三面角,共有四个三面角,可以完全重合,也就是说它们是全等的.正四面体、正六面体、正八面体、正十二面体、正二十面体分别如图所示.
我们可以看到,正多面体每个顶点处有相同数量的棱相交,每一条棱处有两个面相交.
材料2:1996年诺贝尔化学奖授予对发现C60有重大贡献的三位科学家,C60是由60个C原子构成的分子,它是形如足球的多面体,这个多面体有60个顶点,以每一个顶点为端点都有三条棱,面的形状只有五边形和六边形;
(1)阅读上述材料,请用数学符号表示简单多面体的顶点数、棱数及面数,并用相应的数学符号写出多面体欧拉公式(不需要证明);
(2)请结合上述材料,在下面两个问题中选择一个回答,并写出解答过程. (选择问题1分,解答过程正确5分;两个问题都选择,不给分)
问题1:请问C60的分子结构模型中,有几个五边形?
问题2:简单多面体中是否存在正16面体?如果存在请作出它的大致图形并指出面的形状;如果不存在,请说明理由.
参考答案
一、填空题(本大题满分36分)本大题共有12题,只要求直接填写结果,每个空格填对得3分,否则一律得零分.
1.已知定直线,定点,则直线与点确定的平面有 1 个(请填写个数).
2. 已知球的半径为1,则此球的表面积为 .
3. 在装有4个红球和2个白球的盒子中任意取一球,则 “取出的球是白球”为 随机 现象(填“随机”或“确定性”).
4. 已知随机事件A和B不可能同时发生,若,,则P(B)= .
5. 我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 0.98 .
6. “若直线平面,则直线与平面内无数条直线垂直”是 真 命题.(请用“真”,“假”填空)
7. 已知正三棱锥的底面边长为4,高为2,则此三棱锥的体积为
8. 2021年7月24日,在东京奥运会女子10米气步枪决赛中,中国选手杨倩以251.8环的总成绩夺得金牌,为中国代表团摘得本届奥运会首金.已知杨倩其中5次射击命中的环数如下:10.8,10.6,10.6,10.7,9.8,则这组数据的方差为 0.128 .
9. 作直线和平面,则下列小组内两个事件互为对立事件的有 1 组(请填写个数)A组:“”和“”;B组:“为异面直线”和“”;
C组:“或”和“与相交”.
10. 已知随机事件发生的概率满足,小华猜测事件会发生,小明猜测事件不会发生;则以下判读中正确的是 ③ .(请填写序号)
①小华一定猜错;②小华和小明猜对的可能性一样大;③小明猜对的可能性更大;④无法判断小华和小明谁猜对的可能性更大.
11. 已知棱长为4的正方体,动点M在正方体表面上,且满足,则以下结论中正确的是: ② ③ (请填写序号)
①满足条件的点M有且只有6个;②满足条件的点M都在同一个平面上;
③点M的轨迹长度为.
12. 如图,在中,已知,D是斜边AB上任意一点(不含端点)沿直线CD将折成直二面角,当 时,折叠后A、B两点间的距离最小.
二、选择题(本大题满分12分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,每题答对得3分,否则一律得零分.
13.下列调查方式合适的是( C )
A.为了了解一批炮弹的杀伤半径,采用普查的方式
B.为了了解一批玉米种子的发芽率,采用普查的方式
C.为了了解一条河流的水质,采用抽查的方式
D.为了了解一个寝室的学生(共5个人)每周体育锻炼的时间,采用抽查的方式
14.空间中,如果一个角的两边和另一个角的两边分别对应平行,那么这两个角( C )
A.相等 B.互补 C.相等或互补 D.互余
15.军训时,甲、乙两名同学进行射击比赛,共比赛10场,每场比赛各射击四次,且用每场击中环数之和作为该场比赛的成绩.数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图,并给出下列三个结论:
(1)甲的成绩的极差是29;
(2)乙的成绩的众数是21;
(3)乙的成绩的中位数是18.
则这三个结论中,错误结论的个数为(B )
A.0 B.1 C.2 D.3
16.投壶是我国古代的一种娱乐活动,比赛投中得分情况分“有初”,“贯耳”,“散射”,“双耳”,“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为,投中“贯耳”的概率为,投中“散射”的概率为,投中“双耳”的概率为,投中“依竿”的概率为,未投中(筹)的概率为.乙的投掷水平与甲相同,且甲、乙投掷相互独立.比赛第一场,两人平局;第二场甲投中“有初”,乙投中“双耳”,则三场比赛结束时,甲获胜的概率为( A )
A. B. C. D.
三、解答题(本大题满分52分)本大题共有5题,解答下列各题必须写出必要的步骤.
17.(本题满分10分)独立地重复抛掷硬币2次,若每次抛掷硬币正面朝上和反面朝上的概率都是0.5,回答以下两个问题:
(1)现将“独立地重复抛掷硬币2次”作为一次试验,若用分别表示正面朝上和反面朝上,例如用表示某次试验的结果是第一次正面朝上,第二次反面朝上,请用符号写出“独立地重复抛掷硬币2次”的样本空间;
(2)已知在某次试验中第一次抛掷的结果是正面朝上;某同学说“第二次抛掷硬币正面朝上的可能性小于反面朝上的可能性”请问该同学的表述是否正确?(不需要写出理由)
解:(1)
说明:本题6分,如果没有写集合但是元素都表示正确的情况下建议给4分;其它情况题组长酌情处理;
不正确
说明:本题4分
18.(本题满分10分)已知某圆柱底面半径和母线长都是3.
(1)求出该圆柱的表面积和体积;
(2)若圆锥与该圆柱底面半径、高都相等,求圆锥的侧面积
解:(1);
说明:本题6分,面积和体积各3分;答案正确满分,答案不正确但公式正确每个2分;其它情况题组长酌情处理;
(2)
说明:本题4分;答案正确满分,答案不正确但公式正确2分;其它情况题组长酌情处理;
19.(本题满分10分)如图,在正方体中.
(1)求异面直线和所成的角的余弦值;
(2)求证:直线平面.
解:(1)因为,所以就是异面直线和所成的角或其补角.所以异面直线和所成的角为,所以异面直线和所成的角的余弦值为.
说明:本题5分,答案正确满分;答案不正确时找到角并表达正确给3分;题组长酌情处理;
(2)连接,因为,所以四边形为平行四边形,所以;在平面外,在平面内;所以直线平面
说明:本题5分;有辅助线作图或文字表述2分,得出“”2分,结论1分;其它情况题组长酌情处理;
20.(本题满分10分)2020年1月8日,在“不忘初心、牢记使命”主题教育总结大会上,习总书记指出:“要把学习贯彻党的创新理论作为思想武装的重中之重,同学习党史、新中国史、改革开放史、社会主义发展史结合起来。为了提高思想认识,某校开展了“学史明鉴、牢记使命”知识竞赛活动,从950名参赛的学生中随机选取100人的成绩作为样本,得到如图所示的频率分布直方图.
(1)现将全体参赛学生成绩编号为001--950,使用附图提供的“随机数表”从第二行的第三个数开始从左往右抽,请写出前3个被抽到样本编号;
(2)求频率分布直方图中的值,并估计该校此次参赛学生成绩的平均分(同一组数据用该组区间的中点值代表).
解:(1)580;438;908
说明:本题5分,写对1个给1分,写对2个给3分,全部写对给5分;顺序错了不扣分;其它情况题组长酌情处理;
(2);
说明:本题5分,写对给2分,写对给3分;其它情况题组长酌情处理;
21.(本题满分12分,第1问6分,第2问6分)
材料1:三棱锥有4个顶点,6条棱,4个面;正方体有8个顶点,12条棱,6个面;三棱柱有个6顶点,9条棱,5个面;...,通过观察发现:这些几何体的顶点数、棱数及面数都满足简单的规律:4+4-6=8+6-12=6+5-9=2;在此基础上瑞士数学家欧拉证明了对于任意简单多面体,其顶点数、棱数及面数都满足多面体欧拉公式.所谓简单多面体指的是同胚于球面的多面体(同胚可以简单理解为如果在一个多面体内部吹气,它能膨胀变为一个球,那么可以认为它与球同胚).正多面体是指多面体的各个面都是全等的正多边形,并且各个多面角(多面角是指有公共端点且两两不共线的条射线,以及相邻两条射线间的平面部分所组成的图形,例如日常生活中我们看到的墙角就是一个特殊的三面角)都是全等的多面角.例如,正四面体的四个面都是全等的三角形,每个顶点有一个三面角,共有四个三面角,可以完全重合,也就是说它们是全等的.正四面体、正六面体、正八面体、正十二面体、正二十面体分别如图所示.
我们可以看到,正多面体每个顶点处有相同数量的棱相交,每一条棱处有两个面相交.
材料2:1996年诺贝尔化学奖授予对发现C60有重大贡献的三位科学家,C60是由60个C原子构成的分子,它是形如足球的多面体,这个多面体有60个顶点,以每一个顶点为端点都有三条棱,面的形状只有五边形和六边形;
(1)阅读上述材料,请用数学符号表示简单多面体的顶点数、棱数及面数,并用相应的数学符号写出多面体欧拉公式(不需要证明);
(2)请结合上述材料,在下面两个问题中选择一个回答,并写出解答过程. (选择问题1分,解答过程正确5分;两个问题都选择,不给分)
问题1:请问C60的分子机构模型中,有几个五边形?
问题2:简单多面体中是否存在正16面体?如果存在请作出它的大致图形并指出面的形状;如果不存在,请说明理由.
解: (1)设多面体的顶点数为,棱数为,面数为;
则多面体欧拉公式为
说明:本题6分;具体给分方式题组长酌情处理;
(2)问题1:设C60的分子机构模型中,有个五边形, 个五边形
则: ,所以有12个五边形
问题2:设多面体的顶点数为,棱数为,面数为;每个面都是正边形,每个顶点为端点都有条棱.
则,
,不可能都大于4
时, 得 正四面体、正六面体、正十二面体
时, 得 正四面体、正八面体、正二十面体
说明:本题6分;如果两个都选了,按选第一个批改但如果回答错误,选题的1分不给;具体给分方式题组长酌情处理.
11 / 11
同课章节目录
