安徽省芜湖市2021--2022学年人教版九年级上学期期末考试数学试卷(PDF版,含答案)
文档属性
| 名称 | 安徽省芜湖市2021--2022学年人教版九年级上学期期末考试数学试卷(PDF版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 761.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 15:04:12 | ||
图片预览




文档简介
九上期末试卷
一、选择题(本大题共 10 道小题)
1
1. 抛物线 y= x2 2 2,y=x,y=-x 的共同性质是:
2
①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对称轴;④都关于x轴对称.其中正确的个数有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
2.如图,动点 M,N 分别在直线 AB 与 CD 上,且 AB//CD,∠BMN 与∠MND 的平分线相交于点 P,若以 MN 为直
径作⊙O,则点 P与⊙O 的位置关系是( )
器
图
A.点 P在⊙O 外 B.点 P在⊙O内
C.点 P在⊙O 上 D.以上都有可能
y ax2
辑
3. 抛物线 = +bx+c(a≠0)的部分图象如图所示,与 x轴的一个交点坐标为(4,0),抛物线的对称
轴是直线 x 2=1.下列结论中:①abc<0;②2a+b=0;③方程 ax +编bx+c=2 有两个不相等的实数根;④2抛物线与 x轴的另一个交点坐标为(﹣2,0);⑤若点FA(m,n)在该抛物线上,则 am +bm+c≤a+b+c.其中正确的有( )
A.5个 B.P4 个 DC.3 个 D.2个4. 抛物线 y=ax2+bx-3 过点(2,4),则代数式 8a+4b+1 的值为( )A.-2 B.2 C.15 D.-15
2
5. 二次函数 y=ax +bx+c 的图象如图所示,则点 在第___象限( )
云A. 一 B. 二 C. 三 D. 四
风
6. 在 Rt△ABC 中,∠C=90°,BC=3 cm,AC=4 cm,以点 C为圆心,以 2.5 cm 为半径画圆,则⊙C与直
线 AB的位置关系是( )
1 / 7
A. 相交 B. 相切 C. 相离 D. 不能确定
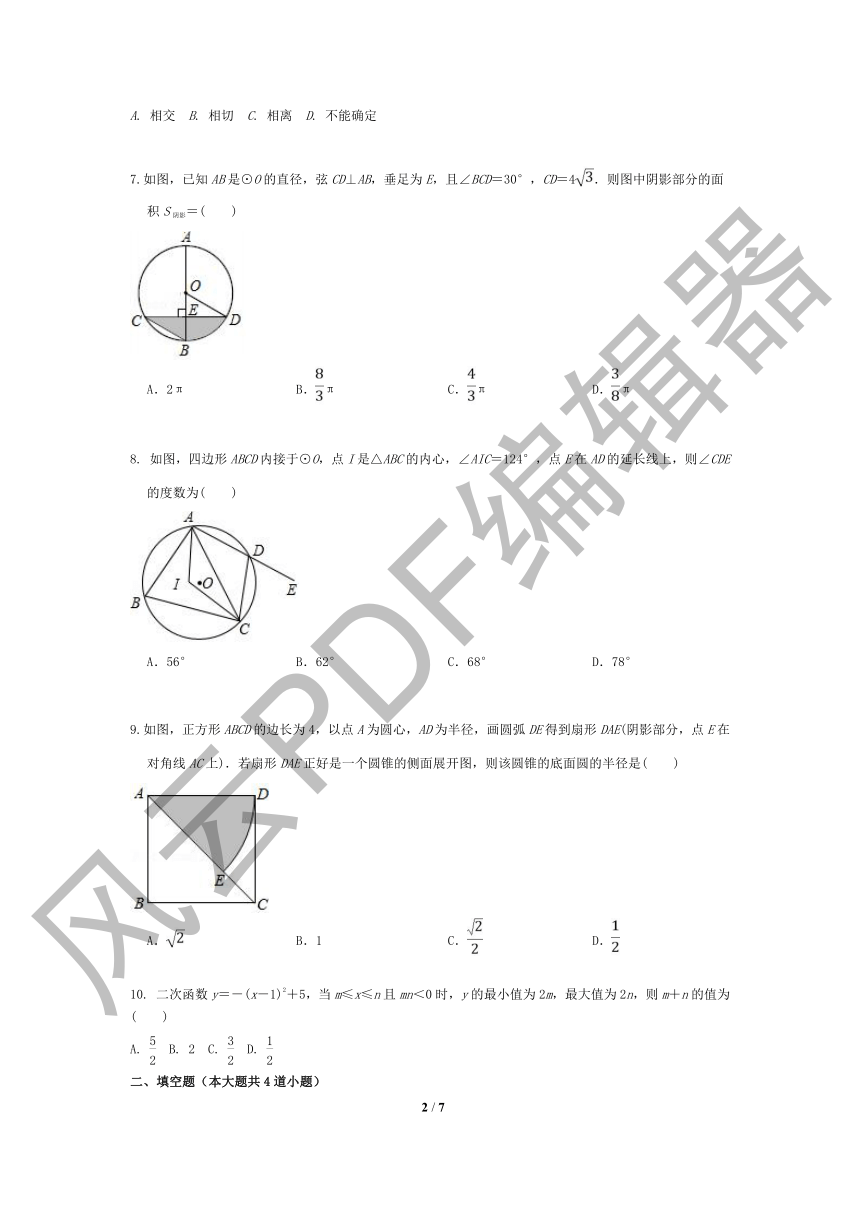
7.如图,已知 AB是⊙O 的直径,弦 CD⊥AB,垂足为 E,且∠BCD=30°,CD=4 .则图中阴影部分的面
积 S 阴影=( )
器
A.2π B. π C. π D. π
8. 如图,四边形 ABCD 内接于⊙O,点 I是△ABC 的内心,∠AIC=124°,点 E在 AD 的延辑长线上,则∠CDE
的度数为( )
F编
A.56° B.62° C.68° D.78°
9.如图,正方形 ABCD 的边长为 4,以点 A为D圆心,AD为半径,画圆弧 DE得到扇形 DAE(阴影部分,点 E在
对角线 AC 上).若扇形 DAE 正P好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
云
风A. B.1 C. D.210. 二次函数 y=-(x-1) +5,当 m≤x≤n且 mn<0时,y的最小值为 2m,最大值为 2n,则 m+n的值为( )
5 3 1
A. B. 2 C. D.
2 2 2
二、填空题(本大题共 4道小题)
2 / 7
2
11. 在 x + +4=0 的横线上添加一个关于 x的一次项,使方程有两个相等的实数根.
3
y y ax212. 如图,已知函数 =- 与 = +bx(a>0,b>0)的图象交于点 P,点 P的纵坐标为 1,则关于 x的方
x
3
2
程 ax +bx+ =0 的解为_______.
x
2 2
13.函数 y=(m ﹣3m+2)x +mx+1﹣m,则当 m= 时,它为正比例函数;当 m= 时,它为一次函数;器
当 m 时,它为二次函数.
14.如图,在平面直角坐标系中,点 P1的坐标为( , ),将线段 OP1绕点 O按顺时针方辑向旋转 45°,再
将其长度伸长为 OP1的 2倍,得到线段 OP2;又将线段 OP2绕点 O按顺时针方向旋转 45°,长度伸长为 OP2
的 2倍,得到线段 OP3;如此下去,得到线段 OP4,OP5,…,OPn(n 为正整编数),则点 P2020的坐标是 .F
三、解答题(本大题共 9道小题) D
x y 2,
15. 解方程组: 2
x 2xy 3yP2 0.
m 2
16.关于 x 的云一元二次方程 x m 3 x m 1 0 有两个实数根4
(1)求 m 的取值范围;
风(2)若 m 为正整数,求此方程的根.
2
17.已知抛物线 y1=ax +bx+c 过点 A(1,0),顶点为 B,且抛物线不经过第三象限.
(1)使用 a、c表示 b;
3 / 7
(2)判断点 B所在象限,并说明理由;
c
(3)若直线 y2=2x+m 经过点 B,且与该抛物线交于另一点 C ,b 8 ,求当 x≥1时 y1的取值范围.
a
18. 如图,AC 是⊙O的直径,PA 切⊙O于点 A,点 B是⊙O上的一点,且∠BAC=30°,∠APB=60°.
(1)求证:PB 是⊙O的切线;
(2)若⊙O 的半径为 2,求弦 AB及 PA,PB 的长.
器
19.在平面直角坐标系中,△ABC 的点坐标分别是 A(2,4)、B(1,2)、C(5,3),如图:辑
(1)以点(0,0)为旋转中心,将△ABC 顺时针转动 90°,得到△A1B1C1,编在坐标系中画出△A1B1C1,写出 A1、B1、C1的坐标;(2)在(1)中,若△ABC 上有一点 P(m,n),直接写出对应点 P1的坐标.
(3)作出△ABC 关于点 O 的中心对称图形△A2B2C2.
PD
F
云
20.将正面分别写有数字 1,2,3 的三张卡片(卡片的形状、大小、质地、颜色等其他方面完全相同)洗匀后,
风背面朝上放在桌面上.甲从中随机抽取一张卡片,记该卡片上的数字为 a,然后放回洗匀,背面朝上放在桌面上;再由乙从中随机抽取一张卡片,记该卡片上的数字为 b,组成数对(a,b).
(1)请写出数对(a,b)所有可能出现的结果;
4 / 7
2
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽取一次卡片,按照得到的数对计算 ab 的值,若
ab2的值为奇数则甲贏;ab2的值为偶数则乙贏.你认为这个游戏公平吗?请说明理由.
21. A、B 两人去茅山风景区游玩,已知每天某一时段开往风景区有三辆舒适程度不同的车,开过来的顺序
也不确定.两人采取了不同的乘车方案: 器
A 无论如何总是上开来的第一辆车;B先观察后上车,当第一辆车开来时他不上车,而是仔细观察车的舒适
度,如果第二辆车的状况比第一辆车好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.
如果把这三辆车的舒适程度分为上、中、下三等,请解决下列问题: 辑
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为 A、B两人采用的方案,哪种方案使自己乘上等车的可能性编大?为什么?
DF
22.一个不透明的盒子中装有两个P红球和一个蓝球.这些球除颜色外都相同.
(1)从中随机摸云出一个球.记下颜色后放回.再从中随机摸出一个球.①请用列表法或树状图法,求第一次摸到蓝球,第二次摸到红球的概率;②请直接写出两次摸到的球的颜色能配成紫色的概率 .
(2)从中随机摸出一个球,记下颜色后不放回.再从中随机摸出一个球,请直接写出两次摸到的球的颜色能
风配成紫色的概率 .
5 / 7
23. 如图,已知△ABC 内接于⊙O,点 C 在劣弧 AB 上(不与点 A,B 重合),点 D 为弦 BC 的中点,DE⊥BC,
DE 与 AC 的延长线交于点 E.射线 AO与射线 EB 交于点 F,与⊙O交于点 G.设∠GAB=α,∠ACB=β,∠EAG
+∠EBA=γ.
(1)点点同学通过画图和测量得到以下近.似.数据
α 30° 40° 50° 60°
β 120° 130° 140° 150°
γ 150° 140° 130° 120°
猜想:β关于α的函数表达式,γ关于α的函数表达式,并给出证明;
(2)若γ=135°,CD=3,△ABE 的面积为△ABC 的面积的 4倍,求⊙O半径的长.
器
辑
DF
编
P
云
风
6 / 7
九上期末试卷-讲评卷
一、选择题(本大题共 10 道小题)
1
y x2 y x2 y x21. 抛物线 = , = , =- 的共同性质是:
2
①都是开口向上;②都以点(0,0)为顶点;③都以 y 轴为对称轴;④都关于 x
轴对称.其中正确的个数有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
1 2 2 2
【答案】B 【解析】抛物线 y= x,y=x,y=-x 的共同性质是:
2
序号 逐项分析 正误器
1 2 2 2
抛物线 y= x,y=x 都是开口向上,但抛物线 y=-x 的开
① 2 ×
口向下,错误 辑
② 三条抛物线都是以(0,0)为顶点,正确 √
③ 三条抛物线都是以 y轴为对称轴,正确 √
④ 三条抛物线都关于 y轴对称,错误 ×
2.如图,动点 M,N 分别在直线 AB与FCD 上,编且 AB//CD,∠BMN 与∠MND 的平分线相交于点 P,若以 MN 为直径作⊙O,则点 P与⊙O的位
置关系是( )
PD
图
A.点 P在云⊙O外 B.点 P在⊙O内C.点 P在⊙O上 D.以上都有可能
风【答案】 C 点拨:∵AB∥CD,∴∠BMN+∠MND=180°,
∵∠BMN 与∠MND 的平分线相交于点 P,
1 / 17
1 1
∴∠PMN= ∠BMN,∠PNM= ∠MND,
2 2
∴∠PMN+∠PNM=90°.
∴∠MPN=180°-(∠PMN+∠PNM)=180°-90°=90°.
1
∴以 MN为直径作⊙O时,OP= MN=⊙O 的半径,
2
∴点 P 在⊙O 上.故选 C.
3. 抛物线 y=ax2+bx+c(a≠0)的部分图象如图所示,与 x轴的一个交点坐标为器
(4,0),抛物线的对称轴是直线 x=1.下列结论中:①abc<0;②2a+b=0;
2
③方程 ax +bx+c=2 有两个不相等的实数根;④抛物线与 x轴的另一个交点坐
2
标为(﹣2,0);⑤若点 A(m,n)在该抛物线上,则 am +bm+c辑≤a+b+c.其
中正确的有( )
编
A.5 个 B.4 个 CF.3个 D.2个【答案】A
解:抛物线开口向下,则 a<0,对称轴在 y轴的右侧,a、b异号,所以 b>0,
抛物线与 y轴交在正半轴,c>0,D因此 abc<0,故①正确;
对称轴 x=1,即﹣ =1,也就是 2a+b=0,因此②正确;
2
抛物线 y=ax +bx+c(a≠P0)的图象与直线 y=2有两个不同交点,因此方程
ax2+bx+c=2 有两个不相等的实数根,故③正确;
抛物线的对云称轴为直线 x=1,与 x轴的一个交点为(4,0),根据对称性可得与 x轴的另一个交点为(﹣2,0),因此④正确;
2 2
风当 x=1时,y=a+b+c 的值最大,当 x=m时,y=am +bm+c,因此 am +bm+c≤a+b+c,故⑤正确.综上所述,正确的结论有①②③④⑤,
2
4. 抛物线 y=ax +bx-3 过点(2,4),则代数式 8a+4b+1 的值为( )
2 / 17
A.-2 B.2 C.15 D.-15
【答案】【答案】C
2
5. 二次函数 y=ax +bx+c 的图象如图所示,则点 在第___象限( )
A. 一 B. 二 C. 三 D. 四
器
【答案】D 辑
6. 在 Rt△ABC 中,∠C=90°,BC=3 cm,AC=4 cm,以点 C为圆心,以 2.5 cm
为半径画圆,则⊙C与直线 AB 的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 不能确定
【答案】 A 【解析】如解图,在 Rt△ABFC 中,AC编=4,BC=3,由勾股定理得1 1AB=5.过 C 作 CD⊥AB 于 D,则 S△ABC= AC·BC= AB·CD,解得 CD=2.4<2.5,∴2 2
直线 AB 与⊙C相交.
PD解图
7.如图,已云知 AB 是⊙O的直径,弦 CD⊥AB,垂足为 E,且∠BCD=30°,CD=4 .则图中阴影部分的面积 S 阴影=( )
风
A.2π B. π C. π D. π
【答案】解:∵AB 是⊙O的直径,弦 CD⊥AB,
3 / 17
∴CE=ED=2 ,
又∵∠DCB=30°,
∴∠DOE=2∠BCD=60°,∠ODE=30°,
∴OE=2 2,OD=2OE=4,
∴S 阴影=S 扇形 BOD﹣S△DOE+S△BEC 2×2 .
故选:B. 器
8. 如图,四边形 ABCD 内接于⊙O,点 I是△ABC 的内心,∠AIC=124°,点 E
在 AD 的延长线上,则∠CDE 的度数为( ) 辑
A.56° B.62° C.68°编D.78°
【答案】解:∵点 I是△ABC 的内心,
∴∠BAC=2∠IAC、∠ACB=2∠ICA, F
∵∠AIC=124°,
∴∠B=180°﹣(∠BAC+∠ACB) D
=180°﹣2(∠IAC+∠ICPA)=180°﹣2(180°﹣∠AIC)
=68°,
又四边形云ABCD 内接于⊙O,∴∠CDE=∠B=68°,
故选:C.
风9.如图,正方形 ABCD 的边长为 4,以点 A为圆心,AD 为半径,画圆弧 DE 得到扇
形 DAE(阴影部分,点 E在对角线 AC 上).若扇形 DAE 正好是一个圆锥的侧面
展开图,则该圆锥的底面圆的半径是( )
4 / 17
A. B.1 C. D.
【答案】解:设圆锥的底面圆的半径为 r,
根据题意可知:
AD=AE=4,∠DAE=45°, 器
底面圆的周长等于弧长:
∴2πr , 辑
解得 r .
答:该圆锥的底面圆的半径是 .
故选:D. 编
2
10. 二次函数 y=-(x-1) +5,当 m≤x≤Fn 且 mn<0 时,y的最小值为 2m,最
大值为 2n,则 m+n的值为( )
5 3 1
A. B. 2 C. D.
2 2 2 D
【答案】D 【解析】结P合题意,先画草图如解图,由题意可知,m<0,n>0,根据 y 2的最小值为 2m,得 2m=-(m-1) +5 ,则 m=-2,根据 y的最大值为 2n,1
得出 2n=5,则 n=2.5,∴m+n= ,故选 D.
云 2
风
二、填空题(本大题共 4道小题)
5 / 17
2
11. 在 x + +4=0 的横线上添加一个关于 x的一次项,使方程有两个相等
的实数根.
【答案】4x(或-4x,只写一个即可) [解析]一元二次方程有两个相等的实根,
则 b2 2-4ac=b -16=0,解得 b=±4,所以一次项为 4x 或-4x.
3 2
12. 如图,已知函数 y=- 与 y=ax +bx(a>0,b>0)的图象交于点 P,
x
P 2
3
点 的纵坐标为 1,则关于 x的方程 ax +bx+ =0 的解为_______.
x 器
辑
【答案】 x=-3 编
2
13.函数 y=(m ﹣3m+2)x2+mx+1﹣m,则当 m=F时,它为正比例函数;当 m=时,它为一次函数;当 m 时,它为二次函数.
2
【答案】解:m﹣3m+2=0,
则(m﹣1)(m﹣2)=0, D
解得:m1=1,m2=2,
故 m≠1且 m≠2时,它为P二次函数;当 m=1或 2时,它为一次函数,当 m=1
时,它为正比例函数;
故答案为:云1;1 或 2;m≠1 且 m≠2
风14.如图,在平面直角坐标系中,点 P1的坐标为( , ),将线段 OP1绕点 O按顺时针方向旋转 45°,再将其长度伸长为 OP1的 2倍,得到线段 OP2;又将线段OP2绕点 O按顺时针方向旋转 45°,长度伸长为 OP2的 2倍,得到线段 OP3;如
此下去,得到线段 OP4,OP5,…,OPn(n 为正整数),则点 P2020的坐标
是 .
6 / 17
【答案】解:∵点 P1的坐标为( , ),将线段 OP1绕点 O按逆时针方向旋转
45°,再将其长度伸长为 OP1的 2倍,得到线段 OP2;
∴OP1=1,OP2=2, 器
∴OP 3 43=4,如此下去,得到线段 OP4=2,OP5=2…,
∴OP n﹣1n=2 ,
由题意可得出线段每旋转 8次旋转一周, 辑
∵2020÷8=252…4,
∴点 P2020的坐标与点 P4的坐标在同一直线上F,正好在编y 轴的负半轴上,∴点 P 20192020的坐标是(0,﹣2 ).2019故答案为:(0,﹣2 ).
三、解答题(本大题共 9道小题)
x y P2, D15. 解方程组: x2 2xy 3y2 0.
x-y=2, ①
【答案】解:
x2 2-2xy-3y =0, ②
方程①变形为 y=x-2. ③
2 2
把③代入②云,得 x-2x(x-2)-3(x-2) =0.x2整理,得 -4x+3=0.
解这个方程,得 x
风 1
=1,x2=3.
将 x1=1,x2=3代入③,分别求得 y1=-1,y2=1.
x1=1, x2=3,
所以原方程组的解为 或
y1=-1 y2=1.
16.关于 x m的一元二次方程 x2 m 3 x m 1 0有两个实数根
4
(1)求m 的取值范围;
(2)若m 为正整数,求此方程的根.
7 / 17
m
0 4 9
【答案】解:(1) 则m 且m 0;
m 3
2 4 m m 5 1 0
4
1
(2)m 1时,原方程为 x2 2x 0,则 x 0或 8。
4
2
17.已知抛物线 y1=ax +bx+c 过点 A(1,0),顶点为 B,且抛物线不经过
第三象限. 器
(1)使用 a、c 表示 b;
(2)判断点 B所在象限,并说明理由; 辑c
(3)若直线 y 2=2x+m 经过点 B,且与该抛物线交于另一点 C ,b 8 ,
a
求当 x≥1 时 y1的取值范围. 编
【答案】 解:(1)把点 A(1,0)的F坐标代入函数解析式即可得到b=-a-c.
(2)若 a<0,则抛物线开口D向下,抛物线必过第三象限,所以 a<0不成立.
当 a>0 时,抛物线开P口向上,B在第四象限.理由如下:由题意,
ax2 bx 2+ +c=0 可变形为 ax -(a+c)x+c=0,
解得 x1=1云,x c2= ,a≠c,a
所以抛物线与 x 轴有两个交点.又因为抛物线不经过第三象限,所以
风a>0,且顶点在第四象限; c(3)由(2)知抛物线与 x 轴两个交点为 A(1,0)与( ,0).a
8 / 17
c
∵直线 y2=2x+m 与该抛物线交于点 B、点 C ( ,b+8),∴点 C就是抛a
2
物线与 x 轴的一个交点,即 b+8=0,b=-8,此时-a-c=-8,y1=ax
4 ac 16
-8x+c,抛物线顶点 B 的坐标为( , ).
a a
把 B、C两点坐标代入直线解析式 y2=2x+m,得 ac+2c=24.
又 a+c=8,解得 a=c=4(与 a≠c矛盾,舍去)或 a=2,c=6.
2
∴y1=2x -8x+6,B(2,-2). 器
画出上述二次函数的图象(如答图),观察图象知,当 x≥1 时,y1的
最小值为顶点纵坐标-2,且无最大值. 辑
编
∴当 x≥1 时,y1的取值范围是 y1≥-F2.
答图
点拨:二次函数的问题通常都D是求解析式、求对称轴、求顶点坐标、
求最值以及与其他知识的综合等,本题基本上综合了上述各种问题,
解题的方法就是牢牢P抓住二次函数的对称轴的求法,顶点坐标的求
法,以及云最值的求法.
18. 如图,AC 是⊙O 的直径,PA 切⊙O于点 A,点 B 是⊙O 上的一点,
风且∠BAC=30°,∠APB=60°.
(1)求证:PB 是⊙O的切线;
9 / 17
(2)若⊙O的半径为 2,求弦 AB 及 PA,PB 的长.
【答案】(1)证明:连接 OB.∵OA=OB,∴∠OBA=∠BAC=30°.∴
∠AOB=180°-30°-30°=120°.∵PA切⊙O于点 A,∴OA⊥PA,∴∠
OAP=90°. 器
∵四边形的内角和为 360°,
∴∠OBP=360°-90°-60°-120°=90°. 辑
∴OB⊥PB.
又∵点 B 是⊙O上的一点, 编
∴PB是⊙O的切线.
(2)解:连接 OP.∵PA、PB 是⊙O 的F切线,∴PA=PB,∠OPA=
1
∠OPB= ∠APB=30°.
2
在 Rt△OAP 中,∠OAPP=90°,D∠OPA=30°,∴OP=2OA=2×2=4,∴PA= OP 2 OA2 = 42 22 =2 3 .
∵PA=PB,∠APB=60°,∴PA=PB=AB=2 3 .
云
风19.在平面直角坐标系中,△ABC 的点坐标分别是 A(2,4)、B(1,2)、C(5,3),如图:(1)以点(0,0)为旋转中心,将△ABC 顺时针转动 90°,得到△A1B1C1,在坐标系
中画出△A1B1C1,写出 A1、B1、C1的坐标;
(2)在(1)中,若△ABC 上有一点 P(m,n),直接写出对应点 P1的坐标.
10 / 17
(3)作出△ABC 关于点 O的中心对称图形△A2B2C2.
【答案】解:(1)如图所示,△A 器1B1C1即为所求,A1(4,﹣2)、B1(2,﹣1)、C1(3,
﹣5);
(2)若△ABC 上有一点 P(m,n),则对应点 P1的坐标为(n,﹣m).
(3)如图所示,△A2B2C2即为所求. 辑
编
DF
20.将正面分别写有数字P1,2,3 的三张卡片(卡片的形状、大小、质地、颜色等
其他方面完全相同)洗匀后,背面朝上放在桌面上.甲从中随机抽取一张卡片,
记该卡云片上的数字为 a,然后放回洗匀,背面朝上放在桌面上;再由乙从中随机抽取一张卡片,记该卡片上的数字为 b,组成数对(a,b).
(1)请写出数对(a,b)所有可能出现的结果;
风(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽取一次卡片,按照得2 2到的数对计算 ab 的值,若 ab 的值为奇数则甲贏;ab2的值为偶数则乙贏.你认为这个游戏公平吗?请说明理由.
【答案】解:(1)如图所示:
11 / 17
2
(2)由树状图知,共有 9种等可能结果,其中 ab 的值为奇数的有 1、9、3、27
2
这 4种结果,ab 的值为偶数的有 4、2、8、18、12 这 5 种结果, 器
所以甲赢的概率为 ,乙赢的概率为 ,
∵ ,
∴这个游戏不公平. 辑
编
21. A、B 两人去茅山风景区游玩,已知每天F某一时段开往风景区有三辆舒适程度不同的车,开过来的顺序也不D确定.两人采取了不同的乘车方案:A无论如何总是上开来的第一辆车;B先观察后上车,当第一辆车开来时他不上车,而是仔细观察车的舒P适度,如果第二辆车的状况比第一辆车好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请解决下列问题:(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为云A、B 两人采用的方案,哪种方案使自己乘上等车的可能性大?为什么?【答案】解:(1)列表:
风
12 / 17
三辆车按出现的先后顺序共有 6种不同的可能;
(2)A 采用的方案使自己乘上等车的概率 ;B采用的方案使自己乘上等车的器
概率 ,
因为 , 辑
所以 B人采用的方案使自己乘上等车的可能性大.
22.一个不透明的盒子中装有两个红球和一个蓝球.编这些球除颜色外都相同.
(1)从中随机摸出一个球.记下颜色后放回.再从中随机摸出一个球.
①请用列表法或树状图法,求第一次摸到蓝F球,第二次摸到红球的概率;
②请直接写出两次摸到的球的颜色能配成紫色的概率 .
(2)从中随机摸出一个球P,记下颜D色后不放回.再从中随机摸出一个球,请直接写出两次摸到的球的颜色能配成紫色的概率 .【答案】解:(1)根据题意画图如下:
云
风①共有 9种等情况数,其中第一次摸到蓝球,第二次摸到红球的有 2种,则第一次摸到蓝球,第二次摸到红球的概率是 ;
②两次摸到的球的颜色能配成紫色的有 4种情况,
则两次摸到的球的颜色能配成紫色的概率是 ;
13 / 17
故答案为: ;
(2)根据题意画图如下:
器
共有 6种等情况数,其中两次摸到的球的颜色能配成紫色的有 4种,
则两次摸到的球的颜色能配成紫色的概率 ;
故答案为: . 辑
23. 如图,已知△ABC 内接于⊙O,点 C 在劣弧 AB 上编(不与点 A,B 重合),点 D为弦 BC 的中点,DE⊥BC,DE 与 AC 的延长线F交于点 E.射线 AO 与射线 EB 交于点F,与⊙O交于点 G.设∠GAB=α,∠ACB=β,∠EAG+∠EBA=γ.(1)点点同学通过画图和测量得到以下近.似.数据α 30°D40° 50° 60°120 130 150β 140°° ° °150 140 120γ 130°° ° °
猜想:β关于α的函数表达式,γ关于α的函数表达式,并给出证明;
(2)若γ=135°,CD=3P,△ABE 的面积为△ABC 的面积的 4倍,求⊙O半径的长.
云
风【答案】【思维教练】(1)观察表格可猜想β=90°+α,γ=180°-α.连接BG,由直径所对的圆周角为 90°和圆内接四边形的对角和为 180°即可得出β=
90°+α;由题干条件易知△EBD≌△EGD,∠EBC=∠ECB,再由三角形的外角和
定理和β=90°+α,利用角度之间的转化即可得出结论;(2)由(1)的结论可以
得出α=∠BAG=45°,β=∠ACB=135°,∴∠ECB=45°,∠CEB=90°,△ECD、
△BEC、△ABG 都是等腰直角三角形,由 CD 的长,可得出 BE 和 CE 的长,再由题
14 / 17
干条件△ABE的面积是△ABC的面积的4倍可得出AC的长,利用勾股定理在△ABE
中求出 AB 的长,再利用勾股定理在△ABG 求出 AG 的长,即可求出半径长.
①
(1)①β=90°+α,γ=180°-α
证明:如解图①,连接 BG,
∵AG 是⊙O的直径,∴∠ABG=90°,
∴α+∠BGA=90°,
又∵四边形 ACBG 内接于⊙O,
∴β+∠BGA=180°,
∴β-α=90°,
即β=90°+α;
②∵D是 BC 的中点,且 DE⊥BC,
∴△EBD≌△ECD,∴∠EBC=∠ECB,
∵∠EAG+∠EBA=γ,
∴∠EAB+α+∠EBC+∠CBA=γ,
∵∠EAB+∠CBA=∠ECB,
∴2∠ECB+α=γ,
∴2(180°-β )+α=γ,
由①β=90°+α代入后化简得,γ=180°-α;
(2)如解图②,连接 BG,
②
∵γ=135°,γ=180°-α,
∴α=45°,β=135°,
∴∠AGB=∠ECB=45°,
∴△ECD 和△ABG 都是等腰直角三角形,
又∵△ABE 的面积是△ABC 的面积的 4倍,
∴AE=4AC,∴EC=3AC,
∵CD=3,∴CE=3 2,AC= 2,∴AE=4 2,(10 分)
∵∠BEA=90°,
2 2 2 2
∴由勾股定理得,AB= BE +AE = (3 2)+(4 2)= 50=5 2,(11 分)
15 / 17
∴AG= 2AB= 2×5 2=10,
∴r=5.
16 / 17
一、选择题(本大题共 10 道小题)
1
1. 抛物线 y= x2 2 2,y=x,y=-x 的共同性质是:
2
①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对称轴;④都关于x轴对称.其中正确的个数有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
2.如图,动点 M,N 分别在直线 AB 与 CD 上,且 AB//CD,∠BMN 与∠MND 的平分线相交于点 P,若以 MN 为直
径作⊙O,则点 P与⊙O 的位置关系是( )
器
图
A.点 P在⊙O 外 B.点 P在⊙O内
C.点 P在⊙O 上 D.以上都有可能
y ax2
辑
3. 抛物线 = +bx+c(a≠0)的部分图象如图所示,与 x轴的一个交点坐标为(4,0),抛物线的对称
轴是直线 x 2=1.下列结论中:①abc<0;②2a+b=0;③方程 ax +编bx+c=2 有两个不相等的实数根;④2抛物线与 x轴的另一个交点坐标为(﹣2,0);⑤若点FA(m,n)在该抛物线上,则 am +bm+c≤a+b+c.其中正确的有( )
A.5个 B.P4 个 DC.3 个 D.2个4. 抛物线 y=ax2+bx-3 过点(2,4),则代数式 8a+4b+1 的值为( )A.-2 B.2 C.15 D.-15
2
5. 二次函数 y=ax +bx+c 的图象如图所示,则点 在第___象限( )
云A. 一 B. 二 C. 三 D. 四
风
6. 在 Rt△ABC 中,∠C=90°,BC=3 cm,AC=4 cm,以点 C为圆心,以 2.5 cm 为半径画圆,则⊙C与直
线 AB的位置关系是( )
1 / 7
A. 相交 B. 相切 C. 相离 D. 不能确定
7.如图,已知 AB是⊙O 的直径,弦 CD⊥AB,垂足为 E,且∠BCD=30°,CD=4 .则图中阴影部分的面
积 S 阴影=( )
器
A.2π B. π C. π D. π
8. 如图,四边形 ABCD 内接于⊙O,点 I是△ABC 的内心,∠AIC=124°,点 E在 AD 的延辑长线上,则∠CDE
的度数为( )
F编
A.56° B.62° C.68° D.78°
9.如图,正方形 ABCD 的边长为 4,以点 A为D圆心,AD为半径,画圆弧 DE得到扇形 DAE(阴影部分,点 E在
对角线 AC 上).若扇形 DAE 正P好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
云
风A. B.1 C. D.210. 二次函数 y=-(x-1) +5,当 m≤x≤n且 mn<0时,y的最小值为 2m,最大值为 2n,则 m+n的值为( )
5 3 1
A. B. 2 C. D.
2 2 2
二、填空题(本大题共 4道小题)
2 / 7
2
11. 在 x + +4=0 的横线上添加一个关于 x的一次项,使方程有两个相等的实数根.
3
y y ax212. 如图,已知函数 =- 与 = +bx(a>0,b>0)的图象交于点 P,点 P的纵坐标为 1,则关于 x的方
x
3
2
程 ax +bx+ =0 的解为_______.
x
2 2
13.函数 y=(m ﹣3m+2)x +mx+1﹣m,则当 m= 时,它为正比例函数;当 m= 时,它为一次函数;器
当 m 时,它为二次函数.
14.如图,在平面直角坐标系中,点 P1的坐标为( , ),将线段 OP1绕点 O按顺时针方辑向旋转 45°,再
将其长度伸长为 OP1的 2倍,得到线段 OP2;又将线段 OP2绕点 O按顺时针方向旋转 45°,长度伸长为 OP2
的 2倍,得到线段 OP3;如此下去,得到线段 OP4,OP5,…,OPn(n 为正整编数),则点 P2020的坐标是 .F
三、解答题(本大题共 9道小题) D
x y 2,
15. 解方程组: 2
x 2xy 3yP2 0.
m 2
16.关于 x 的云一元二次方程 x m 3 x m 1 0 有两个实数根4
(1)求 m 的取值范围;
风(2)若 m 为正整数,求此方程的根.
2
17.已知抛物线 y1=ax +bx+c 过点 A(1,0),顶点为 B,且抛物线不经过第三象限.
(1)使用 a、c表示 b;
3 / 7
(2)判断点 B所在象限,并说明理由;
c
(3)若直线 y2=2x+m 经过点 B,且与该抛物线交于另一点 C ,b 8 ,求当 x≥1时 y1的取值范围.
a
18. 如图,AC 是⊙O的直径,PA 切⊙O于点 A,点 B是⊙O上的一点,且∠BAC=30°,∠APB=60°.
(1)求证:PB 是⊙O的切线;
(2)若⊙O 的半径为 2,求弦 AB及 PA,PB 的长.
器
19.在平面直角坐标系中,△ABC 的点坐标分别是 A(2,4)、B(1,2)、C(5,3),如图:辑
(1)以点(0,0)为旋转中心,将△ABC 顺时针转动 90°,得到△A1B1C1,编在坐标系中画出△A1B1C1,写出 A1、B1、C1的坐标;(2)在(1)中,若△ABC 上有一点 P(m,n),直接写出对应点 P1的坐标.
(3)作出△ABC 关于点 O 的中心对称图形△A2B2C2.
PD
F
云
20.将正面分别写有数字 1,2,3 的三张卡片(卡片的形状、大小、质地、颜色等其他方面完全相同)洗匀后,
风背面朝上放在桌面上.甲从中随机抽取一张卡片,记该卡片上的数字为 a,然后放回洗匀,背面朝上放在桌面上;再由乙从中随机抽取一张卡片,记该卡片上的数字为 b,组成数对(a,b).
(1)请写出数对(a,b)所有可能出现的结果;
4 / 7
2
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽取一次卡片,按照得到的数对计算 ab 的值,若
ab2的值为奇数则甲贏;ab2的值为偶数则乙贏.你认为这个游戏公平吗?请说明理由.
21. A、B 两人去茅山风景区游玩,已知每天某一时段开往风景区有三辆舒适程度不同的车,开过来的顺序
也不确定.两人采取了不同的乘车方案: 器
A 无论如何总是上开来的第一辆车;B先观察后上车,当第一辆车开来时他不上车,而是仔细观察车的舒适
度,如果第二辆车的状况比第一辆车好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.
如果把这三辆车的舒适程度分为上、中、下三等,请解决下列问题: 辑
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为 A、B两人采用的方案,哪种方案使自己乘上等车的可能性编大?为什么?
DF
22.一个不透明的盒子中装有两个P红球和一个蓝球.这些球除颜色外都相同.
(1)从中随机摸云出一个球.记下颜色后放回.再从中随机摸出一个球.①请用列表法或树状图法,求第一次摸到蓝球,第二次摸到红球的概率;②请直接写出两次摸到的球的颜色能配成紫色的概率 .
(2)从中随机摸出一个球,记下颜色后不放回.再从中随机摸出一个球,请直接写出两次摸到的球的颜色能
风配成紫色的概率 .
5 / 7
23. 如图,已知△ABC 内接于⊙O,点 C 在劣弧 AB 上(不与点 A,B 重合),点 D 为弦 BC 的中点,DE⊥BC,
DE 与 AC 的延长线交于点 E.射线 AO与射线 EB 交于点 F,与⊙O交于点 G.设∠GAB=α,∠ACB=β,∠EAG
+∠EBA=γ.
(1)点点同学通过画图和测量得到以下近.似.数据
α 30° 40° 50° 60°
β 120° 130° 140° 150°
γ 150° 140° 130° 120°
猜想:β关于α的函数表达式,γ关于α的函数表达式,并给出证明;
(2)若γ=135°,CD=3,△ABE 的面积为△ABC 的面积的 4倍,求⊙O半径的长.
器
辑
DF
编
P
云
风
6 / 7
九上期末试卷-讲评卷
一、选择题(本大题共 10 道小题)
1
y x2 y x2 y x21. 抛物线 = , = , =- 的共同性质是:
2
①都是开口向上;②都以点(0,0)为顶点;③都以 y 轴为对称轴;④都关于 x
轴对称.其中正确的个数有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
1 2 2 2
【答案】B 【解析】抛物线 y= x,y=x,y=-x 的共同性质是:
2
序号 逐项分析 正误器
1 2 2 2
抛物线 y= x,y=x 都是开口向上,但抛物线 y=-x 的开
① 2 ×
口向下,错误 辑
② 三条抛物线都是以(0,0)为顶点,正确 √
③ 三条抛物线都是以 y轴为对称轴,正确 √
④ 三条抛物线都关于 y轴对称,错误 ×
2.如图,动点 M,N 分别在直线 AB与FCD 上,编且 AB//CD,∠BMN 与∠MND 的平分线相交于点 P,若以 MN 为直径作⊙O,则点 P与⊙O的位
置关系是( )
PD
图
A.点 P在云⊙O外 B.点 P在⊙O内C.点 P在⊙O上 D.以上都有可能
风【答案】 C 点拨:∵AB∥CD,∴∠BMN+∠MND=180°,
∵∠BMN 与∠MND 的平分线相交于点 P,
1 / 17
1 1
∴∠PMN= ∠BMN,∠PNM= ∠MND,
2 2
∴∠PMN+∠PNM=90°.
∴∠MPN=180°-(∠PMN+∠PNM)=180°-90°=90°.
1
∴以 MN为直径作⊙O时,OP= MN=⊙O 的半径,
2
∴点 P 在⊙O 上.故选 C.
3. 抛物线 y=ax2+bx+c(a≠0)的部分图象如图所示,与 x轴的一个交点坐标为器
(4,0),抛物线的对称轴是直线 x=1.下列结论中:①abc<0;②2a+b=0;
2
③方程 ax +bx+c=2 有两个不相等的实数根;④抛物线与 x轴的另一个交点坐
2
标为(﹣2,0);⑤若点 A(m,n)在该抛物线上,则 am +bm+c辑≤a+b+c.其
中正确的有( )
编
A.5 个 B.4 个 CF.3个 D.2个【答案】A
解:抛物线开口向下,则 a<0,对称轴在 y轴的右侧,a、b异号,所以 b>0,
抛物线与 y轴交在正半轴,c>0,D因此 abc<0,故①正确;
对称轴 x=1,即﹣ =1,也就是 2a+b=0,因此②正确;
2
抛物线 y=ax +bx+c(a≠P0)的图象与直线 y=2有两个不同交点,因此方程
ax2+bx+c=2 有两个不相等的实数根,故③正确;
抛物线的对云称轴为直线 x=1,与 x轴的一个交点为(4,0),根据对称性可得与 x轴的另一个交点为(﹣2,0),因此④正确;
2 2
风当 x=1时,y=a+b+c 的值最大,当 x=m时,y=am +bm+c,因此 am +bm+c≤a+b+c,故⑤正确.综上所述,正确的结论有①②③④⑤,
2
4. 抛物线 y=ax +bx-3 过点(2,4),则代数式 8a+4b+1 的值为( )
2 / 17
A.-2 B.2 C.15 D.-15
【答案】【答案】C
2
5. 二次函数 y=ax +bx+c 的图象如图所示,则点 在第___象限( )
A. 一 B. 二 C. 三 D. 四
器
【答案】D 辑
6. 在 Rt△ABC 中,∠C=90°,BC=3 cm,AC=4 cm,以点 C为圆心,以 2.5 cm
为半径画圆,则⊙C与直线 AB 的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 不能确定
【答案】 A 【解析】如解图,在 Rt△ABFC 中,AC编=4,BC=3,由勾股定理得1 1AB=5.过 C 作 CD⊥AB 于 D,则 S△ABC= AC·BC= AB·CD,解得 CD=2.4<2.5,∴2 2
直线 AB 与⊙C相交.
PD解图
7.如图,已云知 AB 是⊙O的直径,弦 CD⊥AB,垂足为 E,且∠BCD=30°,CD=4 .则图中阴影部分的面积 S 阴影=( )
风
A.2π B. π C. π D. π
【答案】解:∵AB 是⊙O的直径,弦 CD⊥AB,
3 / 17
∴CE=ED=2 ,
又∵∠DCB=30°,
∴∠DOE=2∠BCD=60°,∠ODE=30°,
∴OE=2 2,OD=2OE=4,
∴S 阴影=S 扇形 BOD﹣S△DOE+S△BEC 2×2 .
故选:B. 器
8. 如图,四边形 ABCD 内接于⊙O,点 I是△ABC 的内心,∠AIC=124°,点 E
在 AD 的延长线上,则∠CDE 的度数为( ) 辑
A.56° B.62° C.68°编D.78°
【答案】解:∵点 I是△ABC 的内心,
∴∠BAC=2∠IAC、∠ACB=2∠ICA, F
∵∠AIC=124°,
∴∠B=180°﹣(∠BAC+∠ACB) D
=180°﹣2(∠IAC+∠ICPA)=180°﹣2(180°﹣∠AIC)
=68°,
又四边形云ABCD 内接于⊙O,∴∠CDE=∠B=68°,
故选:C.
风9.如图,正方形 ABCD 的边长为 4,以点 A为圆心,AD 为半径,画圆弧 DE 得到扇
形 DAE(阴影部分,点 E在对角线 AC 上).若扇形 DAE 正好是一个圆锥的侧面
展开图,则该圆锥的底面圆的半径是( )
4 / 17
A. B.1 C. D.
【答案】解:设圆锥的底面圆的半径为 r,
根据题意可知:
AD=AE=4,∠DAE=45°, 器
底面圆的周长等于弧长:
∴2πr , 辑
解得 r .
答:该圆锥的底面圆的半径是 .
故选:D. 编
2
10. 二次函数 y=-(x-1) +5,当 m≤x≤Fn 且 mn<0 时,y的最小值为 2m,最
大值为 2n,则 m+n的值为( )
5 3 1
A. B. 2 C. D.
2 2 2 D
【答案】D 【解析】结P合题意,先画草图如解图,由题意可知,m<0,n>0,根据 y 2的最小值为 2m,得 2m=-(m-1) +5 ,则 m=-2,根据 y的最大值为 2n,1
得出 2n=5,则 n=2.5,∴m+n= ,故选 D.
云 2
风
二、填空题(本大题共 4道小题)
5 / 17
2
11. 在 x + +4=0 的横线上添加一个关于 x的一次项,使方程有两个相等
的实数根.
【答案】4x(或-4x,只写一个即可) [解析]一元二次方程有两个相等的实根,
则 b2 2-4ac=b -16=0,解得 b=±4,所以一次项为 4x 或-4x.
3 2
12. 如图,已知函数 y=- 与 y=ax +bx(a>0,b>0)的图象交于点 P,
x
P 2
3
点 的纵坐标为 1,则关于 x的方程 ax +bx+ =0 的解为_______.
x 器
辑
【答案】 x=-3 编
2
13.函数 y=(m ﹣3m+2)x2+mx+1﹣m,则当 m=F时,它为正比例函数;当 m=时,它为一次函数;当 m 时,它为二次函数.
2
【答案】解:m﹣3m+2=0,
则(m﹣1)(m﹣2)=0, D
解得:m1=1,m2=2,
故 m≠1且 m≠2时,它为P二次函数;当 m=1或 2时,它为一次函数,当 m=1
时,它为正比例函数;
故答案为:云1;1 或 2;m≠1 且 m≠2
风14.如图,在平面直角坐标系中,点 P1的坐标为( , ),将线段 OP1绕点 O按顺时针方向旋转 45°,再将其长度伸长为 OP1的 2倍,得到线段 OP2;又将线段OP2绕点 O按顺时针方向旋转 45°,长度伸长为 OP2的 2倍,得到线段 OP3;如
此下去,得到线段 OP4,OP5,…,OPn(n 为正整数),则点 P2020的坐标
是 .
6 / 17
【答案】解:∵点 P1的坐标为( , ),将线段 OP1绕点 O按逆时针方向旋转
45°,再将其长度伸长为 OP1的 2倍,得到线段 OP2;
∴OP1=1,OP2=2, 器
∴OP 3 43=4,如此下去,得到线段 OP4=2,OP5=2…,
∴OP n﹣1n=2 ,
由题意可得出线段每旋转 8次旋转一周, 辑
∵2020÷8=252…4,
∴点 P2020的坐标与点 P4的坐标在同一直线上F,正好在编y 轴的负半轴上,∴点 P 20192020的坐标是(0,﹣2 ).2019故答案为:(0,﹣2 ).
三、解答题(本大题共 9道小题)
x y P2, D15. 解方程组: x2 2xy 3y2 0.
x-y=2, ①
【答案】解:
x2 2-2xy-3y =0, ②
方程①变形为 y=x-2. ③
2 2
把③代入②云,得 x-2x(x-2)-3(x-2) =0.x2整理,得 -4x+3=0.
解这个方程,得 x
风 1
=1,x2=3.
将 x1=1,x2=3代入③,分别求得 y1=-1,y2=1.
x1=1, x2=3,
所以原方程组的解为 或
y1=-1 y2=1.
16.关于 x m的一元二次方程 x2 m 3 x m 1 0有两个实数根
4
(1)求m 的取值范围;
(2)若m 为正整数,求此方程的根.
7 / 17
m
0 4 9
【答案】解:(1) 则m 且m 0;
m 3
2 4 m m 5 1 0
4
1
(2)m 1时,原方程为 x2 2x 0,则 x 0或 8。
4
2
17.已知抛物线 y1=ax +bx+c 过点 A(1,0),顶点为 B,且抛物线不经过
第三象限. 器
(1)使用 a、c 表示 b;
(2)判断点 B所在象限,并说明理由; 辑c
(3)若直线 y 2=2x+m 经过点 B,且与该抛物线交于另一点 C ,b 8 ,
a
求当 x≥1 时 y1的取值范围. 编
【答案】 解:(1)把点 A(1,0)的F坐标代入函数解析式即可得到b=-a-c.
(2)若 a<0,则抛物线开口D向下,抛物线必过第三象限,所以 a<0不成立.
当 a>0 时,抛物线开P口向上,B在第四象限.理由如下:由题意,
ax2 bx 2+ +c=0 可变形为 ax -(a+c)x+c=0,
解得 x1=1云,x c2= ,a≠c,a
所以抛物线与 x 轴有两个交点.又因为抛物线不经过第三象限,所以
风a>0,且顶点在第四象限; c(3)由(2)知抛物线与 x 轴两个交点为 A(1,0)与( ,0).a
8 / 17
c
∵直线 y2=2x+m 与该抛物线交于点 B、点 C ( ,b+8),∴点 C就是抛a
2
物线与 x 轴的一个交点,即 b+8=0,b=-8,此时-a-c=-8,y1=ax
4 ac 16
-8x+c,抛物线顶点 B 的坐标为( , ).
a a
把 B、C两点坐标代入直线解析式 y2=2x+m,得 ac+2c=24.
又 a+c=8,解得 a=c=4(与 a≠c矛盾,舍去)或 a=2,c=6.
2
∴y1=2x -8x+6,B(2,-2). 器
画出上述二次函数的图象(如答图),观察图象知,当 x≥1 时,y1的
最小值为顶点纵坐标-2,且无最大值. 辑
编
∴当 x≥1 时,y1的取值范围是 y1≥-F2.
答图
点拨:二次函数的问题通常都D是求解析式、求对称轴、求顶点坐标、
求最值以及与其他知识的综合等,本题基本上综合了上述各种问题,
解题的方法就是牢牢P抓住二次函数的对称轴的求法,顶点坐标的求
法,以及云最值的求法.
18. 如图,AC 是⊙O 的直径,PA 切⊙O于点 A,点 B 是⊙O 上的一点,
风且∠BAC=30°,∠APB=60°.
(1)求证:PB 是⊙O的切线;
9 / 17
(2)若⊙O的半径为 2,求弦 AB 及 PA,PB 的长.
【答案】(1)证明:连接 OB.∵OA=OB,∴∠OBA=∠BAC=30°.∴
∠AOB=180°-30°-30°=120°.∵PA切⊙O于点 A,∴OA⊥PA,∴∠
OAP=90°. 器
∵四边形的内角和为 360°,
∴∠OBP=360°-90°-60°-120°=90°. 辑
∴OB⊥PB.
又∵点 B 是⊙O上的一点, 编
∴PB是⊙O的切线.
(2)解:连接 OP.∵PA、PB 是⊙O 的F切线,∴PA=PB,∠OPA=
1
∠OPB= ∠APB=30°.
2
在 Rt△OAP 中,∠OAPP=90°,D∠OPA=30°,∴OP=2OA=2×2=4,∴PA= OP 2 OA2 = 42 22 =2 3 .
∵PA=PB,∠APB=60°,∴PA=PB=AB=2 3 .
云
风19.在平面直角坐标系中,△ABC 的点坐标分别是 A(2,4)、B(1,2)、C(5,3),如图:(1)以点(0,0)为旋转中心,将△ABC 顺时针转动 90°,得到△A1B1C1,在坐标系
中画出△A1B1C1,写出 A1、B1、C1的坐标;
(2)在(1)中,若△ABC 上有一点 P(m,n),直接写出对应点 P1的坐标.
10 / 17
(3)作出△ABC 关于点 O的中心对称图形△A2B2C2.
【答案】解:(1)如图所示,△A 器1B1C1即为所求,A1(4,﹣2)、B1(2,﹣1)、C1(3,
﹣5);
(2)若△ABC 上有一点 P(m,n),则对应点 P1的坐标为(n,﹣m).
(3)如图所示,△A2B2C2即为所求. 辑
编
DF
20.将正面分别写有数字P1,2,3 的三张卡片(卡片的形状、大小、质地、颜色等
其他方面完全相同)洗匀后,背面朝上放在桌面上.甲从中随机抽取一张卡片,
记该卡云片上的数字为 a,然后放回洗匀,背面朝上放在桌面上;再由乙从中随机抽取一张卡片,记该卡片上的数字为 b,组成数对(a,b).
(1)请写出数对(a,b)所有可能出现的结果;
风(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽取一次卡片,按照得2 2到的数对计算 ab 的值,若 ab 的值为奇数则甲贏;ab2的值为偶数则乙贏.你认为这个游戏公平吗?请说明理由.
【答案】解:(1)如图所示:
11 / 17
2
(2)由树状图知,共有 9种等可能结果,其中 ab 的值为奇数的有 1、9、3、27
2
这 4种结果,ab 的值为偶数的有 4、2、8、18、12 这 5 种结果, 器
所以甲赢的概率为 ,乙赢的概率为 ,
∵ ,
∴这个游戏不公平. 辑
编
21. A、B 两人去茅山风景区游玩,已知每天F某一时段开往风景区有三辆舒适程度不同的车,开过来的顺序也不D确定.两人采取了不同的乘车方案:A无论如何总是上开来的第一辆车;B先观察后上车,当第一辆车开来时他不上车,而是仔细观察车的舒P适度,如果第二辆车的状况比第一辆车好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请解决下列问题:(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为云A、B 两人采用的方案,哪种方案使自己乘上等车的可能性大?为什么?【答案】解:(1)列表:
风
12 / 17
三辆车按出现的先后顺序共有 6种不同的可能;
(2)A 采用的方案使自己乘上等车的概率 ;B采用的方案使自己乘上等车的器
概率 ,
因为 , 辑
所以 B人采用的方案使自己乘上等车的可能性大.
22.一个不透明的盒子中装有两个红球和一个蓝球.编这些球除颜色外都相同.
(1)从中随机摸出一个球.记下颜色后放回.再从中随机摸出一个球.
①请用列表法或树状图法,求第一次摸到蓝F球,第二次摸到红球的概率;
②请直接写出两次摸到的球的颜色能配成紫色的概率 .
(2)从中随机摸出一个球P,记下颜D色后不放回.再从中随机摸出一个球,请直接写出两次摸到的球的颜色能配成紫色的概率 .【答案】解:(1)根据题意画图如下:
云
风①共有 9种等情况数,其中第一次摸到蓝球,第二次摸到红球的有 2种,则第一次摸到蓝球,第二次摸到红球的概率是 ;
②两次摸到的球的颜色能配成紫色的有 4种情况,
则两次摸到的球的颜色能配成紫色的概率是 ;
13 / 17
故答案为: ;
(2)根据题意画图如下:
器
共有 6种等情况数,其中两次摸到的球的颜色能配成紫色的有 4种,
则两次摸到的球的颜色能配成紫色的概率 ;
故答案为: . 辑
23. 如图,已知△ABC 内接于⊙O,点 C 在劣弧 AB 上编(不与点 A,B 重合),点 D为弦 BC 的中点,DE⊥BC,DE 与 AC 的延长线F交于点 E.射线 AO 与射线 EB 交于点F,与⊙O交于点 G.设∠GAB=α,∠ACB=β,∠EAG+∠EBA=γ.(1)点点同学通过画图和测量得到以下近.似.数据α 30°D40° 50° 60°120 130 150β 140°° ° °150 140 120γ 130°° ° °
猜想:β关于α的函数表达式,γ关于α的函数表达式,并给出证明;
(2)若γ=135°,CD=3P,△ABE 的面积为△ABC 的面积的 4倍,求⊙O半径的长.
云
风【答案】【思维教练】(1)观察表格可猜想β=90°+α,γ=180°-α.连接BG,由直径所对的圆周角为 90°和圆内接四边形的对角和为 180°即可得出β=
90°+α;由题干条件易知△EBD≌△EGD,∠EBC=∠ECB,再由三角形的外角和
定理和β=90°+α,利用角度之间的转化即可得出结论;(2)由(1)的结论可以
得出α=∠BAG=45°,β=∠ACB=135°,∴∠ECB=45°,∠CEB=90°,△ECD、
△BEC、△ABG 都是等腰直角三角形,由 CD 的长,可得出 BE 和 CE 的长,再由题
14 / 17
干条件△ABE的面积是△ABC的面积的4倍可得出AC的长,利用勾股定理在△ABE
中求出 AB 的长,再利用勾股定理在△ABG 求出 AG 的长,即可求出半径长.
①
(1)①β=90°+α,γ=180°-α
证明:如解图①,连接 BG,
∵AG 是⊙O的直径,∴∠ABG=90°,
∴α+∠BGA=90°,
又∵四边形 ACBG 内接于⊙O,
∴β+∠BGA=180°,
∴β-α=90°,
即β=90°+α;
②∵D是 BC 的中点,且 DE⊥BC,
∴△EBD≌△ECD,∴∠EBC=∠ECB,
∵∠EAG+∠EBA=γ,
∴∠EAB+α+∠EBC+∠CBA=γ,
∵∠EAB+∠CBA=∠ECB,
∴2∠ECB+α=γ,
∴2(180°-β )+α=γ,
由①β=90°+α代入后化简得,γ=180°-α;
(2)如解图②,连接 BG,
②
∵γ=135°,γ=180°-α,
∴α=45°,β=135°,
∴∠AGB=∠ECB=45°,
∴△ECD 和△ABG 都是等腰直角三角形,
又∵△ABE 的面积是△ABC 的面积的 4倍,
∴AE=4AC,∴EC=3AC,
∵CD=3,∴CE=3 2,AC= 2,∴AE=4 2,(10 分)
∵∠BEA=90°,
2 2 2 2
∴由勾股定理得,AB= BE +AE = (3 2)+(4 2)= 50=5 2,(11 分)
15 / 17
∴AG= 2AB= 2×5 2=10,
∴r=5.
16 / 17
同课章节目录
