北师大版数学五年级上册第四单元多边形的面积测试卷(含答案)
文档属性
| 名称 | 北师大版数学五年级上册第四单元多边形的面积测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 10:46:25 | ||
图片预览


文档简介
第四单元测试卷
时间:60分钟 满分:100分
题号 一 二 三 四 五 六 总分
得分
一、填空。(每空1分,共18分)
1.两个( )的三角形可以拼成一个平行四边形。可知,拼成的平行四边形的底就是原三角形的( ),平行四边形的高就是原三角形的( ),所以三角形的面积就是拼成的平行四边形面积的( ),即三角形面积=( )。
2.一个三角形的面积是24厘米2,高是6厘米,底是( )厘米。
3.一个直角三角形,它的两条直角边长分别是6cm和8cm,直角所对应的斜边长10cm,斜边上的高是( )cm。
4.一个梯形的面积是320dm2,上底和下底的和是40dm,它的高是( )dm。
5.一个平行四边形的面积是12m2,如果把它的底和高都扩大到原来的2倍,得到的平行四边形的面积是( )m2。
6.一个平行四边形面积是35平方厘米,与它等底等高的三角形面积是( )cm2。
7.一个平行四边形比它等底等高的三角形大7.8cm2,平行四边形的面积是( )cm2。
8.一个平行四边形的底是5米,面积是45平方米,它的高是( )米。
9.一个平行四边形的面积是60cm2,如果它的高缩小3倍,底不变,面积是( )cm2。
10.一个等边三角形的周长是18厘米,高是3.6厘米,它的面积是( )平方厘米。
11.一个平行四边形和三角形的面积相等,底也相等,如果平行四边形的高是8cm,那么三角形的高是( )cm。
12.右图平行四边形的面积是( )cm2。(单位:cm)
13.三角形的底是12.6分米,高是底的1.5倍,它的面积是( )。
14.一等腰直角三角形的直角边长是4.8米,它的面积是( )米2。
二、选择题。(20分)
1.如图平行四边形中,未知的高应是( )厘米。
A.9 B.8 C.12 D.15
2.一个直角三角形的三条边长分别为3分米、4分米和5分米。它的面积是( )平方分米。
A.3×4÷2 B.3×5÷2 C.4×5÷2
3.一个梯形的高是4厘米,上底和下底都增加6厘米,面积增加( )。
A.6平方厘米 B.12平方厘米 C.24平方厘米
4.右图平行四边形中,丙的面积是58cm2,平行四边形面积是( )cm2。
A.29 B.58 C.116
5.下面图中长方形和平行四边形的面积相比,( )。
A.长方形大 B.同样大 C.平行四边形大
6.如图中,一组平行线间有甲乙丙三个图形,其中面积最大的是( )。
A.甲 B.乙 C.丙
7.一堆钢管,最上层4根,最下层10根,相邻两层均相差1根,这堆钢管共( )。
A.35根 B.42根 C.49根
8.把一个平行四边形的活动框架拉成一个长方形,那么原来的平行四边形与现在的长方形相比,( )。
A.周长不变,面积不变 B.周长变了,面积不变
C.周长不变,面积变了 D.周长变了,面积变了
9.一个三角形的底不变,要使它的面积扩大4倍,高应扩大( )。
A.2倍 B.4倍 C.6倍
10.三角形和平行四边形的高相等,面积也相等,三角形的底是18cm,平行四边形的底是( )cm。
A.18 B.36 C.9
三、判断题。(10分)
1.一个平行四边形的底扩大3.5倍,高不变,则面积扩大3.5倍。 ( )
2.任何一个梯形都可以分成两个等高的三角形。 ( )
3.三角形的面积是平行四边形面积的一半。 ( )
4.等底等高的三角形面积一定相等,形状也一定相同。 ( )
5.一个平行四边形的底扩大4倍,高缩小2倍,那么面积就扩大2倍。 ( )
6.平行四边形的底越长,它的面积就越大。 ( )
7.一个平行四边形的底是12m,高是4dm,它的面积是48?。 ( )
8.两个三角形面积相等,底和高也一定相等。 ( )
9.两个面积相等的梯形可以拼成一个平行四边形。 ( )
10.边长是4厘米的正方形,它的周长和面积相等。 ( )
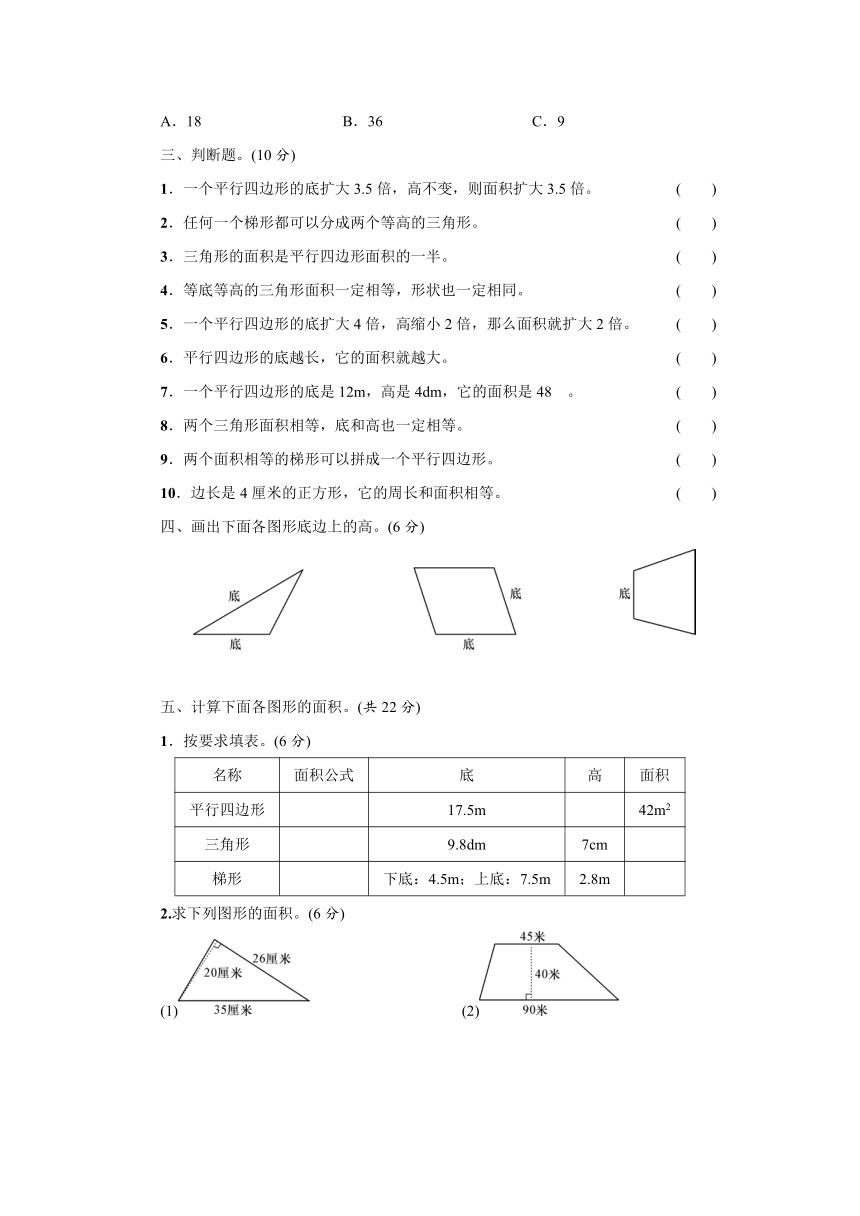
四、画出下面各图形底边上的高。(6分)
五、计算下面各图形的面积。(共22分)
1.按要求填表。(6分)
名称 面积公式 底 高 面积
平行四边形 17.5m 42m2
三角形 9.8dm 7cm
梯形 下底:4.5m;上底:7.5m 2.8m
2.求下列图形的面积。(6分)
(1) (2)
3.求下列阴影部分的面积。(10分)
(1)如图,求图中阴影部分的面积。(单位:厘米)
(2)如图,平行四边形面积为240平方厘米,求阴影部分面积。
六、解决问题。(24分)
1.一块近似平行四边形的草坪,中间有一条石子路(如右图)。如果铺1平方米草坪12.5元,铺这块草坪大约需要多少钱?(4分)
2.梯形的上底是17厘米,下底是23厘米,面积是120平方厘米,梯形的高是多少厘米?(4分)
3.一块三角形广告牌,底长12m,高是4.3m。如果要用油漆刷这块广告牌,共刷油漆19.35kg,这块广告牌每平方米要用油漆多少千克?(4分)
4.王叔叔利用篱笆和一面墙围成了一个菜园,如图所示,篱笆长24m,求这个菜园的面积。(4分)
5.已知等腰三角形的周长为16厘米,腰长5厘米,底边上的高是4厘米,三角形的面积是多少?(4分)
6.有一个直角梯形,它的下底为22厘米,若上底增加8厘米就成为一个正方形,求原来梯形的面积。(4分)
参考答案
第四单元测试卷
一、1.完全相同 底 高 一半 底×高÷2
2.8 3.4.8 4.16 5.48
6.17.5 7.15.6 8.9 9.20
10.10.8 11.16 12.18 13.119.07分米2 14.11.52
二、1.B 解析:平行四边形的面积=底×高,那10×4=5×未知的高=40,未知的高=40÷5=8,注意哪条底对应哪条高。
2.A 解析:三角形的面积=底×高÷2,这个直角三角的底和高是两条直角边,分别为3和4,所以三角形的面积=3×4÷2。
3.C 解析:梯形的面积=(上底+下底)×高÷2,根据已知条件,,上底和下底都增加6厘米,高不变,那么现在梯形的面积=(上底+6+下底+6)×高÷2,相当于面积增加了12×4÷2=24(厘米2)。
4.C 解析:平行四边形面积=丙×2=58×2=116(cm2)。
5.B 解析:长方形和平行四边形等底等高,所以面积相等。
6.B 解析:三个图形高一样,设为h,那么S三角形=12h÷2=6h,S平行四边形=7h,S梯形=(3+8)h÷2=5.5h,7h>6h>5.5h,所以面积最大的是平行四边形。
7.C 解析:(4+10)×7÷2=49(根)。
8.C 9.B
10.C 解析:三角形和平行四边形的高相等,面积也相等,那么三角形的底是平行四边形的底的2倍,那么平行四边形的底=18÷2=9(cm)。
三、1.√ 2.√
3.× 解析:等底等高的三角形的面积是平行四边形面积的一半。
4.× 解析:等底等高的三角形面积一定相等,形状不一定相同。
5.√
6.× 解析:平行四边形的面积大小,不仅要看底还要看高。
7.× 解析:一个平行四边形的底是12m,高是4dm=0.4m,它的面积是4.8m2。
8.× 解析:两个三角形面积相等,底和高不一定相等。
9.× 解析:两个完全相同的梯形可以拼成一个平行四边形。
10.× 解析:边长是4厘米的正方形,它的周长是16cm,面积是16cm2。
四、略
五、1.S=ah 2.4m S=ah 343cm2 S=(a+b)h 16.8m2
2.(1)26×20÷2=260(cm2) (2)(45+90)×40÷2=2700(m2)
3.(1)(3+6)×6÷2=27(cm2) (2)底:240÷12=20(cm) S阴影:(20-15)×12÷2=30(cm2)
六、1.20×9=180(m2) 9×1=9(m2) (180-9)×12.5=2137.5(元)
2.120×2÷(17+23)=240÷40=6(cm)
3.12×4.3÷2=25.8(m2) 19.35÷25.8=0.75(kg)
4.24-8=16(m) 16×8÷2=64(m2)
5.底:16-5×2=6(cm) 6×4÷2=12(cm2)
6.22-8=14(cm) (14+22)×22÷2=36×11=396(cm2)
时间:60分钟 满分:100分
题号 一 二 三 四 五 六 总分
得分
一、填空。(每空1分,共18分)
1.两个( )的三角形可以拼成一个平行四边形。可知,拼成的平行四边形的底就是原三角形的( ),平行四边形的高就是原三角形的( ),所以三角形的面积就是拼成的平行四边形面积的( ),即三角形面积=( )。
2.一个三角形的面积是24厘米2,高是6厘米,底是( )厘米。
3.一个直角三角形,它的两条直角边长分别是6cm和8cm,直角所对应的斜边长10cm,斜边上的高是( )cm。
4.一个梯形的面积是320dm2,上底和下底的和是40dm,它的高是( )dm。
5.一个平行四边形的面积是12m2,如果把它的底和高都扩大到原来的2倍,得到的平行四边形的面积是( )m2。
6.一个平行四边形面积是35平方厘米,与它等底等高的三角形面积是( )cm2。
7.一个平行四边形比它等底等高的三角形大7.8cm2,平行四边形的面积是( )cm2。
8.一个平行四边形的底是5米,面积是45平方米,它的高是( )米。
9.一个平行四边形的面积是60cm2,如果它的高缩小3倍,底不变,面积是( )cm2。
10.一个等边三角形的周长是18厘米,高是3.6厘米,它的面积是( )平方厘米。
11.一个平行四边形和三角形的面积相等,底也相等,如果平行四边形的高是8cm,那么三角形的高是( )cm。
12.右图平行四边形的面积是( )cm2。(单位:cm)
13.三角形的底是12.6分米,高是底的1.5倍,它的面积是( )。
14.一等腰直角三角形的直角边长是4.8米,它的面积是( )米2。
二、选择题。(20分)
1.如图平行四边形中,未知的高应是( )厘米。
A.9 B.8 C.12 D.15
2.一个直角三角形的三条边长分别为3分米、4分米和5分米。它的面积是( )平方分米。
A.3×4÷2 B.3×5÷2 C.4×5÷2
3.一个梯形的高是4厘米,上底和下底都增加6厘米,面积增加( )。
A.6平方厘米 B.12平方厘米 C.24平方厘米
4.右图平行四边形中,丙的面积是58cm2,平行四边形面积是( )cm2。
A.29 B.58 C.116
5.下面图中长方形和平行四边形的面积相比,( )。
A.长方形大 B.同样大 C.平行四边形大
6.如图中,一组平行线间有甲乙丙三个图形,其中面积最大的是( )。
A.甲 B.乙 C.丙
7.一堆钢管,最上层4根,最下层10根,相邻两层均相差1根,这堆钢管共( )。
A.35根 B.42根 C.49根
8.把一个平行四边形的活动框架拉成一个长方形,那么原来的平行四边形与现在的长方形相比,( )。
A.周长不变,面积不变 B.周长变了,面积不变
C.周长不变,面积变了 D.周长变了,面积变了
9.一个三角形的底不变,要使它的面积扩大4倍,高应扩大( )。
A.2倍 B.4倍 C.6倍
10.三角形和平行四边形的高相等,面积也相等,三角形的底是18cm,平行四边形的底是( )cm。
A.18 B.36 C.9
三、判断题。(10分)
1.一个平行四边形的底扩大3.5倍,高不变,则面积扩大3.5倍。 ( )
2.任何一个梯形都可以分成两个等高的三角形。 ( )
3.三角形的面积是平行四边形面积的一半。 ( )
4.等底等高的三角形面积一定相等,形状也一定相同。 ( )
5.一个平行四边形的底扩大4倍,高缩小2倍,那么面积就扩大2倍。 ( )
6.平行四边形的底越长,它的面积就越大。 ( )
7.一个平行四边形的底是12m,高是4dm,它的面积是48?。 ( )
8.两个三角形面积相等,底和高也一定相等。 ( )
9.两个面积相等的梯形可以拼成一个平行四边形。 ( )
10.边长是4厘米的正方形,它的周长和面积相等。 ( )
四、画出下面各图形底边上的高。(6分)
五、计算下面各图形的面积。(共22分)
1.按要求填表。(6分)
名称 面积公式 底 高 面积
平行四边形 17.5m 42m2
三角形 9.8dm 7cm
梯形 下底:4.5m;上底:7.5m 2.8m
2.求下列图形的面积。(6分)
(1) (2)
3.求下列阴影部分的面积。(10分)
(1)如图,求图中阴影部分的面积。(单位:厘米)
(2)如图,平行四边形面积为240平方厘米,求阴影部分面积。
六、解决问题。(24分)
1.一块近似平行四边形的草坪,中间有一条石子路(如右图)。如果铺1平方米草坪12.5元,铺这块草坪大约需要多少钱?(4分)
2.梯形的上底是17厘米,下底是23厘米,面积是120平方厘米,梯形的高是多少厘米?(4分)
3.一块三角形广告牌,底长12m,高是4.3m。如果要用油漆刷这块广告牌,共刷油漆19.35kg,这块广告牌每平方米要用油漆多少千克?(4分)
4.王叔叔利用篱笆和一面墙围成了一个菜园,如图所示,篱笆长24m,求这个菜园的面积。(4分)
5.已知等腰三角形的周长为16厘米,腰长5厘米,底边上的高是4厘米,三角形的面积是多少?(4分)
6.有一个直角梯形,它的下底为22厘米,若上底增加8厘米就成为一个正方形,求原来梯形的面积。(4分)
参考答案
第四单元测试卷
一、1.完全相同 底 高 一半 底×高÷2
2.8 3.4.8 4.16 5.48
6.17.5 7.15.6 8.9 9.20
10.10.8 11.16 12.18 13.119.07分米2 14.11.52
二、1.B 解析:平行四边形的面积=底×高,那10×4=5×未知的高=40,未知的高=40÷5=8,注意哪条底对应哪条高。
2.A 解析:三角形的面积=底×高÷2,这个直角三角的底和高是两条直角边,分别为3和4,所以三角形的面积=3×4÷2。
3.C 解析:梯形的面积=(上底+下底)×高÷2,根据已知条件,,上底和下底都增加6厘米,高不变,那么现在梯形的面积=(上底+6+下底+6)×高÷2,相当于面积增加了12×4÷2=24(厘米2)。
4.C 解析:平行四边形面积=丙×2=58×2=116(cm2)。
5.B 解析:长方形和平行四边形等底等高,所以面积相等。
6.B 解析:三个图形高一样,设为h,那么S三角形=12h÷2=6h,S平行四边形=7h,S梯形=(3+8)h÷2=5.5h,7h>6h>5.5h,所以面积最大的是平行四边形。
7.C 解析:(4+10)×7÷2=49(根)。
8.C 9.B
10.C 解析:三角形和平行四边形的高相等,面积也相等,那么三角形的底是平行四边形的底的2倍,那么平行四边形的底=18÷2=9(cm)。
三、1.√ 2.√
3.× 解析:等底等高的三角形的面积是平行四边形面积的一半。
4.× 解析:等底等高的三角形面积一定相等,形状不一定相同。
5.√
6.× 解析:平行四边形的面积大小,不仅要看底还要看高。
7.× 解析:一个平行四边形的底是12m,高是4dm=0.4m,它的面积是4.8m2。
8.× 解析:两个三角形面积相等,底和高不一定相等。
9.× 解析:两个完全相同的梯形可以拼成一个平行四边形。
10.× 解析:边长是4厘米的正方形,它的周长是16cm,面积是16cm2。
四、略
五、1.S=ah 2.4m S=ah 343cm2 S=(a+b)h 16.8m2
2.(1)26×20÷2=260(cm2) (2)(45+90)×40÷2=2700(m2)
3.(1)(3+6)×6÷2=27(cm2) (2)底:240÷12=20(cm) S阴影:(20-15)×12÷2=30(cm2)
六、1.20×9=180(m2) 9×1=9(m2) (180-9)×12.5=2137.5(元)
2.120×2÷(17+23)=240÷40=6(cm)
3.12×4.3÷2=25.8(m2) 19.35÷25.8=0.75(kg)
4.24-8=16(m) 16×8÷2=64(m2)
5.底:16-5×2=6(cm) 6×4÷2=12(cm2)
6.22-8=14(cm) (14+22)×22÷2=36×11=396(cm2)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
